上一篇写的是BFS问题,今天解决了一道经典的DFS例题素数环。在我来看,DFS和BFS最大的区别就在D和B之间,以D优先就是从一个节点走到底,要么出解要么进死胡同,进了死胡同再回溯到最近的活结点换条路走到黑。以B优先就是同一层可以扩展的节点同时扩展。在解决平面问题比如数独问题和面积问题的时候使用BFS会相对好思考一些。
问题描述:把从1到n这n个数摆成一个环,要求相邻的两个数之和为一个素数,1<=n<=20。输出一个素数环(两个数字间用空格隔开),要求输出字典序中最大的那一个。比如:
输入:4 输出:4 3 2 1
算法思路:因为我们要输出的是字典序中最大的那一个,我们不妨令a[0]为n然后倒着往回退,依次在a[1]尝试从n到1的所有数满足和前一个数之和不为素数、数字没有被使用过的条件则填入,然后再递归的调用函数来填入剩下的。
for(int i = n; i >= 1 && !ans; i--){
if(isPrime(a[k-1]+i) && !exist(a, 0, k-1, i)){
a[k] = i;
fill(k+1);
}
}
很明显本题的剪枝函数就是对前后数素数的判断函数isPrime(),限界函数就是限定每个数字只能使用一次的函数exist()。最后在输出结果前一定要再做一次环的判断,头尾两个数组元素之和也要是素数。源代码如下:
#include <iostream>
using namespace std;
const int NMAX = 20;
int a[NMAX], n;
bool ans = false;
//判断是否为素数,true为是,false为不是
bool isPrime(int x){
for(int i = 2; i*i <= x && x%i != 0; i++);
if(x%i == 0)
return false;
else
return true;
}
//判断从a[0]到a[k-1]是否存在准备填入的数
bool exist(int a[], int start, int end, int x){
bool conf = false;
for(int i = start; i <= end; i++){
if(a[i] == x)
conf = true;
}
return conf;
}
//打印素数环
void prt(int a[], int n){
for(int i = 0; i < n; i++)
cout <<a[i]<<" ";
cout <<endl;
}
void fill(int k){
if(k == n){
//别忘了这是一个环
if(isPrime(a[0]+a[k-1])){
ans = true;
prt(a, n);
}
return;
}
for(int i = n; i >= 1 && !ans; i--){
if(isPrime(a[k-1]+i) && !exist(a, 0, k-1, i)){
a[k] = i;
prt(a, n);
fill(k+1);
}
}
return;
}
int main(){
cin >>n;
a[0] = n;
fill(1);
return 0;
}
当n为8时整个素数环的产生的过程如下,我们可以很清楚的看到整个回溯的过程。
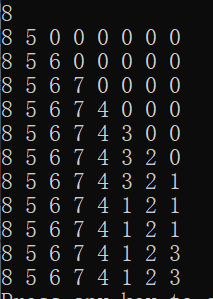





 本文探讨了使用深度优先搜索(DFS)算法解决经典问题——素数环。目标是在1到n的数字中找到一个环形排列,使任意相邻两数之和为素数,并输出字典序最大解。通过倒序填充和回溯策略,实现高效求解。
本文探讨了使用深度优先搜索(DFS)算法解决经典问题——素数环。目标是在1到n的数字中找到一个环形排列,使任意相邻两数之和为素数,并输出字典序最大解。通过倒序填充和回溯策略,实现高效求解。
















 913
913

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








