New程序媛OpenGL全解析之—矩阵基础

大家好

今天丹丹要给大家带来的是矩阵的基础知识。

本期视频的链接地址是：

https://www.bilibili.com/video/av23894103/

大家也可以直接在bi站首页搜索：New程序媛 ，即可看到相应视频

本期没有资源和代码下载链接，因为篇幅原因，怕一篇推问显得过干，所以今天只有矩阵基本知识的内容，下一期的推送会紧紧跟上，在下期推文中给大家放出链接

视频搭配文章一起效果更赞哦

---

---

---

---

在线性代数中，矩阵就是以行和列的形式组成的矩形数据块，向量被看作是一维数组，此时矩阵就是存放多个向量的二维数组。

矩阵的维度被定义为包含了多少行和多少列。

矩阵是使用方括号括起来的r行c列数据块，例如，一个4×3的矩阵：

方阵

对于行数和列数相同的矩阵叫做方阵，如2×2，3×3，4×4，在方阵元素中，行号和列号相同的统称为对角线元素，例如以下方阵：

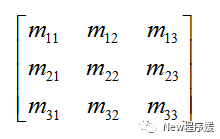
其中， m11，m22，m33就是该3×3方阵的对角线元素。

对角矩阵

除了对角线元素外，方阵的其他元素都为0，那么称这种方阵叫做对角矩阵。例如：

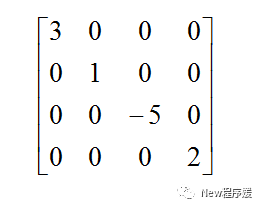
单位矩阵

当对角矩阵的对角线元素都为1，其他元素为0时，就是单位矩阵，即对于n维的单位矩阵可以记作In，是n×n矩阵，单位矩阵的一个重要性质：一个矩阵乘以单位矩阵，将得到原矩阵。比如：

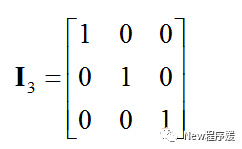
转置矩阵

设一个矩阵M是一个r×c的矩阵，对于M的转置矩阵记作MT，是一个c×r矩阵，它的列由M的行所组成，表示为MijT =Mji，即沿着矩阵的对角线翻折,例如：

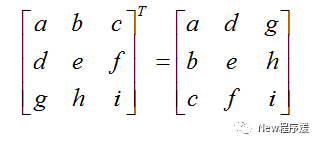
对于任意矩阵M，当这个矩阵转置，再进行一次转置，则所得矩阵为原矩阵，即(MT)T=M。对于任意对角矩阵D来说，DT=D。

标量与矩阵的乘法

设矩阵M和标量k相乘，实际上就是标量k与矩阵中各个分量相乘，结果得到一个和M维数一样的矩阵。一般写法是标量写在矩阵的左边，不用写乘号，如：

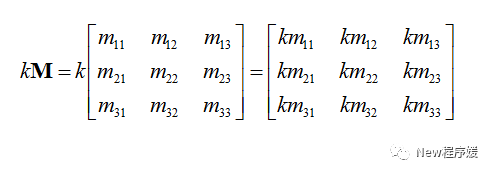
矩阵的乘法

设两个矩阵A，B，当A的列数和B的行数相等时，可以进行乘法运算。若A是一个r×n的矩阵，B为一个n×c的矩阵，那么两向量相乘结果得到一个r×c矩阵，对于矩阵的乘法运算结果记作AB。

设C为A，B两向量相乘结果向量，则C的任意元素Cij等于A的第i行向量与B的第j列向量的点积，记作：

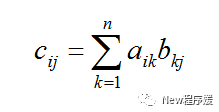
上述公式提取A的第i行和B的第j列，将行和列中的对应元素相乘，然后将结果相加（等于A的i行和B的j列的点乘）所得的和就是Cij，例如：

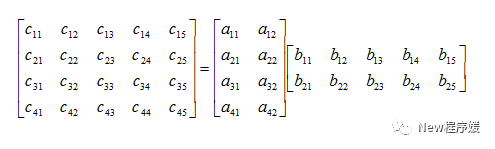
这是4×2的矩阵A和2×5的矩阵B相乘得到4×5的矩阵C

矩阵的乘法不满足交换律：AB≠BA。

矩阵的乘法满足结合律：（AB）C＝A（BC）（前提是矩阵A，B，C的维数使乘法可行）。

矩阵乘法满足与标量或向量的结合律。

 (kA)B=k(AB)=A(kB)    (vA)B=v(AB)

向量与矩阵的乘法

向量可以作为矩阵来表示,所以向量和矩阵也可以做乘法，比如：

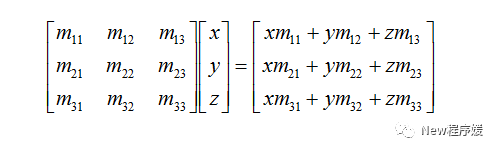
向量与矩阵相乘时需要注意：结果向量中的每一个元素都是原向量与矩阵中单独行或列的点积。矩阵与向量的乘法满足对向量加法的分配律，即对于向量v、w和矩阵M，有（v＋w）M＝vM＋wM。还要注意行向量与列向量的区别。

矩阵的行列式

在任意的方阵中都存在一个标量，这个标量就叫做矩阵的行列式。设方阵M的行列式记作|M|或“det M”。2×2的矩阵行列式，将主对角线和反对角线上的元素各自相乘，然后用主对角线元素的积减去反对角线元素的积：

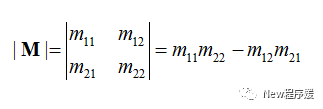
3×3矩阵的行列式定义：

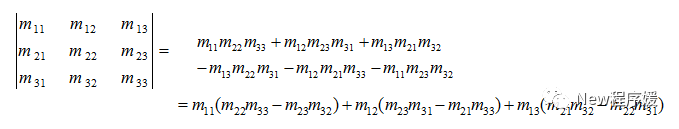
如果是n阶方阵则需要通过降阶的方式求解

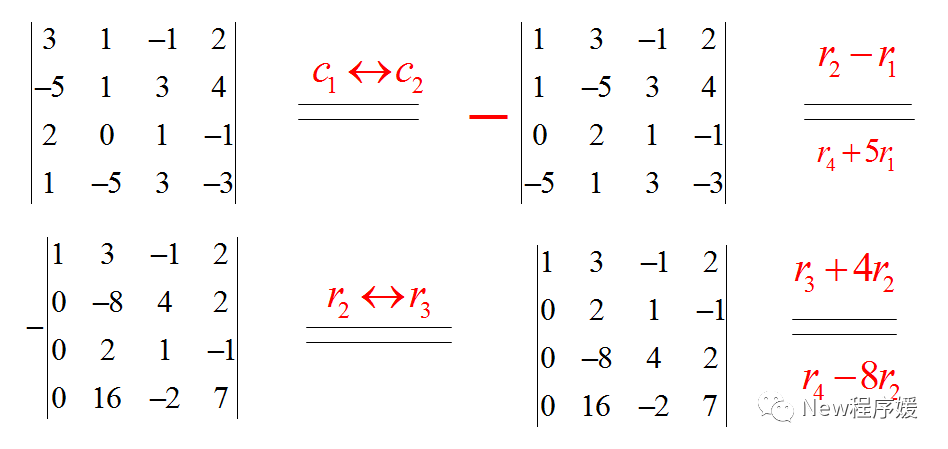
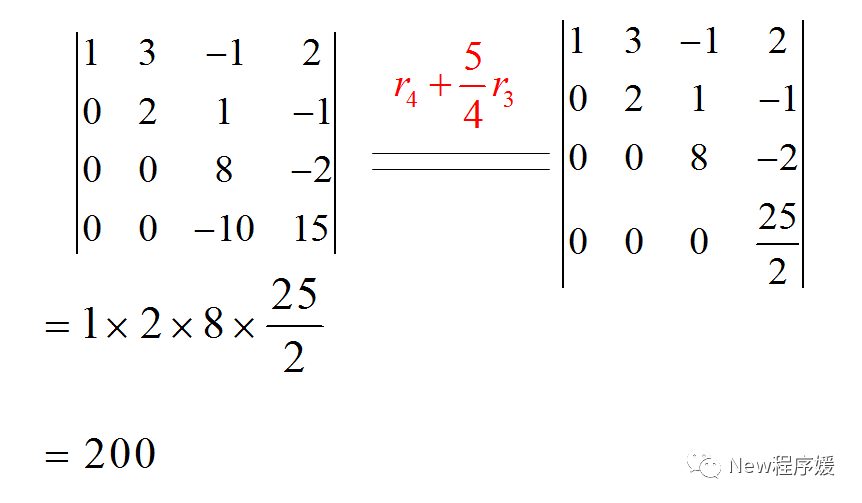
伴随矩阵

由n阶方阵A的行列式|A|的各个元素的代数余子式所构成的n阶方阵称为A的伴随矩阵，简称为伴随阵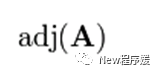

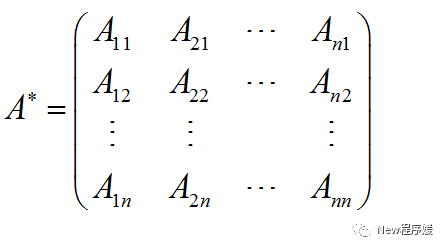
如下示例来求解伴随矩阵：

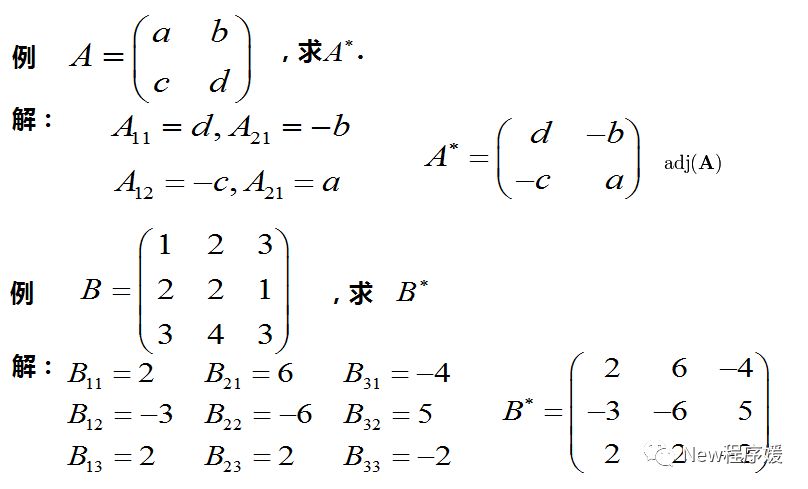
逆矩阵

A为n阶方阵，若存在n阶方阵B，使AB = BA =E则称方阵A可逆，B称为A的逆矩阵。如果A是可逆的，那么的A的逆矩阵是唯一的。

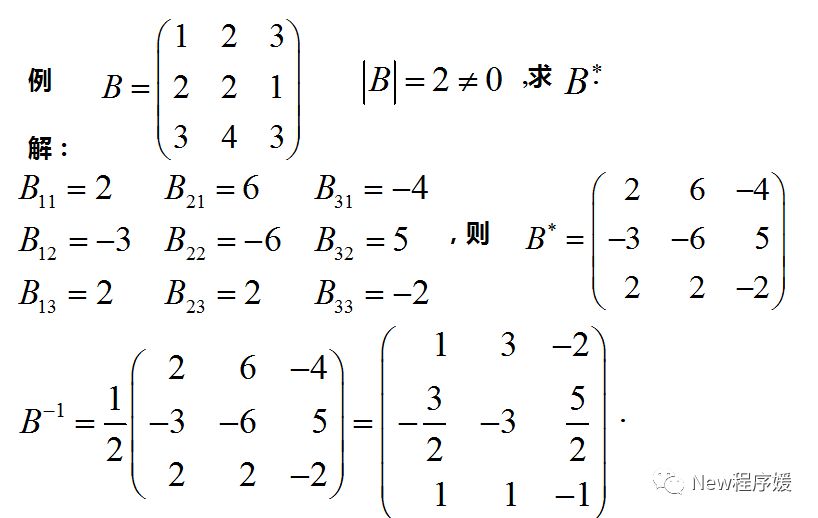
好啦，矩阵基础知道到此就结束啦~ 下一期我们再来给大家讲解旋转平移缩放这些常用矩阵的推导，并把它应用到我们的代码中去

丹丹期待大家的意见和建议，欢迎小伙伴们积极留言