【第3章-数据结构与算法】

3.1线性结构

线性结构的特点是数据集合中的元素之间是一种线性关系，数据元素“一个接一个的排列”，也就是一个序列。

3.1.1线性表

线性表是指一个序列，常采用2种储存方法：顺序存储和链式存储，主要基本操作是插入、删除和查找。

1. 线性表的定义

2. 线性表的存储结构

（1）线性表的顺序存储

第i个元素存储位置：LOC(ai)=LOC(ai)+（i-1）×L

LOC(ai):表示线性表中第一个元素存储位置

L：表示每个元素所占空间的大小

（2）线性表的链式存储

头结点：不存储数据元素的结点，称为头结点

3.1.2 栈和队列

栈按“后进先出”的规则进行修改，队列按“先进先出”的规则进行修改

1. 栈

（1）栈的定义及基本运算

（2）栈的存储结构：栈的循序存储结构、栈的链式存储结构、栈的应用

计算应用：（后进先出）

2. 队列

（1）队列的定义及基本运算

基本运算：

（2）队列的存储结构

1-队列的顺序存储

队列的尾指针所指下一位置是头指针，表示队列满。

如图3-7（f）所示，头、尾指针的值相同时表示队列为空

2-队列的链式存储

3-队列的应用

队列常用于处理需要排队的场合，如操作系统中处理打印任务的打印队列、离散事件的计算机模拟。

3.1.3 串

字符串时一串文字及符号的简称，是一种特殊的线性表。字符串的基本数据元素是字符，计算机中非数值问题处理的对象经常是字符串数据。

如在汇编和高级语言的编译程序中，源程序和目标程序都是字符串数据。

1. 串的定义及基本运算

2. 串的存储结构

（1）顺序存储：该方式是用一组地址连续的存储单元来存储串值的字符序列。

（2）链式存储

3. 字符串运算

4. 串的模式匹配

3.2数组和矩阵

数组可以看成是线性表的推广，其特点是多维数组的数据元素仍然是一个表。

1. 数组

（1）数组的定义及基本运算

一维数组是长度固定的线性表，数组中的每个数据元素类型相同。n维数组是定长线性表在维数上的扩张，即线性表中的元素又是一个线性表。

（2）数组的顺序存储

2. 矩阵

（1）特殊矩阵

常见的特殊矩阵有对称矩阵、三角矩阵和对角矩阵等。

（2）稀疏矩阵

3.3树和图

3.3.1树

树结构是一种非常重要的非线性结构，该结构中的一个数据元素可以有两个或两个以上的直接后继元素，可以用来描述客观世界中广泛存在的层次关系。

1. 树的定义

数是n（n>=0）个结点的有限集合。当n=0时称为空树

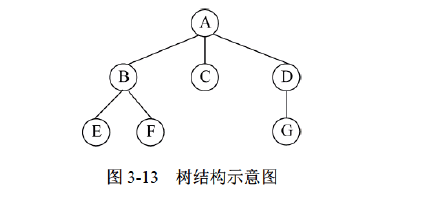
结点的度：一个结点子树的个数记为度

叶子结点：即终端结点，指度为0的结点

树的高度：即为度的深度，上图所示深度为3

有序树：各子树从左到右有次序，即不能交换

森林：m（m>=0）棵互不相交的树的集合

2. 二叉树的定义

二叉树中结点的最大度数为2，而树中不限制结点的度数。

二叉树在结点为1的情况下也要区分左右子树，而普通树不用。

3. 二叉树的性质

性质1：

性质2：

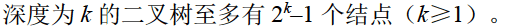
性质3：

性质4：

4. 二叉树的存储结构

（1）二叉树的循序存储结构

（2）二叉树的链式存储结构

5. 二叉树的遍历

二叉树的前序、中序和后序三种遍历方法。

遍历是按照某种策略访问树中的每个结点，且仅访问一次

6. 最优二叉树

最优二叉树又称为哈夫曼树，是一类带权路径长度最短的树。

从树中一个结点到另一个结点之间的通路称为结点间的路径，通路上的分支称为路径长度。

7. 二叉查找树

3.3.2图

图结构中，任意两个结点之间可能有直接的关系，图中一个结点的前驱和后继的数目是没有限制的。

1. 图的定义及术语

图G是由两个集合V和E构成的二元组，记做G=（V,E），其中V是图中顶点的非空有限集合，E是图中边的有限集合。

2. 图的存储结构

（1）邻接矩阵表示法（2）邻接链表表示法

3.4 常用算法

3.4.1算法概述

1. 算法的基本概念

算法是求解过程的精准描述，它为解决某一特定类型的问题规定了一个运算过程。

具有下列特性：（1）有穷性（2）确定性（3）可行性（4）输入（5）输出

算法实质上是特定问题的可行性的求解方法、规则和步骤。

算法优劣考查：（1）正确性（2）可读性（3）健壮性（4）效率

2. 算法与数据结构

数据结构+算法=程序

3. 算法的描述

常用算法描述方法：

（1）流程图

（2）N/S盒图

（3）伪代码

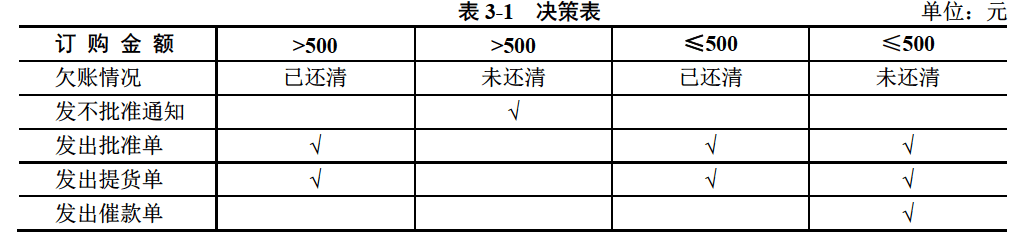
（4）决策表

4. 算法效率

3.4.2排序

1. 简单排序

（1）直接插入排序

（2）冒泡排序

2. 希尔排序

3. 快速排序

4. 堆排序

5. 归并排序

6. 内部排序方法小结

3.4.3查找

1. 查找表及查找效率

2. 顺序查找

3. 折半查找

4. 索引顺序查找

5. 树表查找

6. 哈希查找

3.4.4 递归算法

3.4.5 图的相关算法

1. 求最小生成树算法

2. 拓扑排序

3. 求单源的最短路径算法