CTR之FM、FFM、DeepFM

背景：

• 在传统的线性模型中，每个特征都是独立的，如果需要考虑特征与特征之间的相互作用，可能需要人工对特征进行交叉组合；
• 非线性SVM可以对特征进行核变换，但是在特征高度稀疏的情况下，并不能很好的进行学习；
• 综上提出了FM系列算法

FM

数据模型上表达特征xi，xj的组合用xixj表示，即所说的多项式模型，通常情况下只考虑两阶多项式模型，也就是特征两两组合的问题，模型表达如下：
$$y={\omega }_0+\sum _{i=1}^n{\omega }_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n{\omega }_{ij}{x}_i{x}_j$$
${\omega }_{ij}$求解的思路是通过矩阵分解的方法，引入辅助向量$V_i=(v_{i1},v_{i2},...,v_{ik})$，

然后用$V_i{V}_j^T$对${\omega }_{ij}$进行求解：

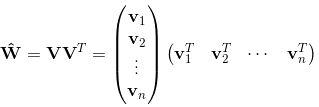
从上式可以看出二项式的参数数量由原来的$\frac{n(n-1)}{2}$个减少为$nk$个，远少于多项式模型的参数数量。另外，参数因子化使得$x_h{x}_i$的参数和$x_h{x}_j$的参数不再相互独立，因为有了$x_h$特征关联。因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。
具体来说，$x_h{x}_i$和$x_h{x}_j$的系数分别为$⟨v_h,v_i⟩,⟨v_h,v_j⟩$,它们之间的共同项$v_h$,因此所有包含$x_h$的非零组合特征的样本都可以用来学习隐向量$v_h$，很大程度上避免了数据稀疏性造成的影响。
求解$⟨v_i,v_j⟩$，具体过程如下，仿照$(a+b+c{)}^2-a^2-b^2-c^2$：

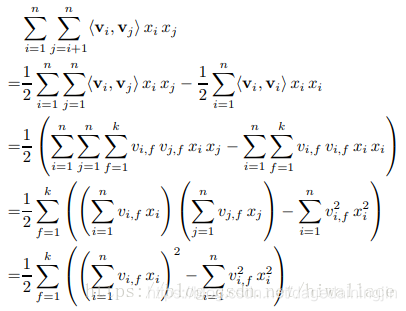
通过上述等式，FM的二次项化简为只与$v_{i,f}$有关的等式。因此，FM可以在线性时间对新样本做出预测，复杂度和LR模型一样，且效果提升不少。
在训练FM时，假如使用SGD来优化模型，训练时各个参数的梯度如下：

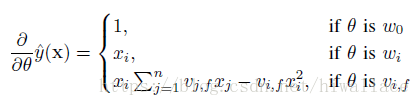
FFM

1.原理

在CTR预估中，通常会遇到one-hot类型的变量，会导致数据特征的稀疏。为解决这个问题，FFM在FM的基础上进一步改进，在模型中引入类别的概念，即field。将同一个field的特征单独进行one-hot，因此在FFM中，每一维特征（假设$n$个）都会针对其他特征的每个field（假设$f$个），分别学习一个隐变量（总共$nf$个），该隐变量不仅与特征相关，也与field相关。
假设样本的$n$个特征属于$f$个field，那么FFM的二次项有$nf$个隐向量，相当于每个特征有$f$个隐变量。而在FM模型中，每个特征的隐向量只有一个。FM可以看做FFM的特例，把所有特征都归属到一个field的FFM模型。其模型方程为：
$$y={\omega }_0+\sum _{i=1}^n{\omega }_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n⟨V_{i,f_j},V_{j,f_i}⟩x_i{x}_j$$
FM中$x_i{x}_j$的系数$⟨V_i,V_j⟩$在FFM中变为$⟨V_{i,f_j},V_{j,f_i}⟩$，主要是增加了一层field，所有$V_{i,f_j},V_{j,f_i}$取自于以下矩阵：
$$T={\left(\begin{array}{cccc}{V}_{11}& V_{12}& \cdots & V_{1f}\\ V_{21}& V_{22}& \cdots & V_{2f}\\ ⋮& ⋮& & ⋮\\ V_{n1}& V_{n2}& \cdots & V_{nf}\end{array}\right)}_{n\times f}$$
而他们具体形式同FM，为

所以，FFM的二次参数有$nfk$个，远多于FM模型的$nk$个。

2.应用

CTR应用中常出现以下三类特征：

• 用户相关的特征
  年龄、性别、职业、兴趣、品类偏好、浏览/购买品类等基本信息，以及用户近期点击量/购买量/消费额等统计信息
• 商品相关的特征
  商品所属品类、销量、价格、评分、历史CTR/CVR等信息
• 用户-商品匹配特征
  浏览/购买品类匹配、浏览/购买商家匹配、兴趣偏好匹配等

为了使用FFM方法，所有的特征必须转换成“field_id:feat_id:value”格式，field_id代表特征所属field的编号，feat_id是特征编号，value是特征的值。

• 数值型的特征比较容易处理，只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等。
• categorical特征需要经过One-Hot编码成数值型，编码产生的所有特征同属于一个field，而特征的值只能是0或1，如用户的性别、年龄段，商品的品类id等。
• 除此之外，还有第三类特征，如用户浏览/购买品类，有多个品类id且用一个数值衡量用户浏览或购买每个品类商品的数量。这类特征按照categorical特征处理，不同的只是特征的值不是0或1，而是代表用户浏览或购买数量的数值。按前述方法得到field_id之后，再对转换后特征顺序编号，得到feat_id，特征的值也可以按照之前的方法获得。

实例

• 原始数据
  
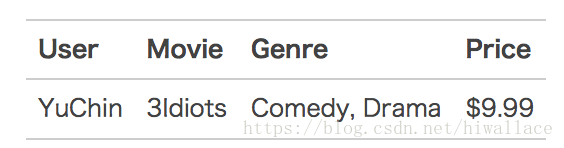
• 特征编号
  
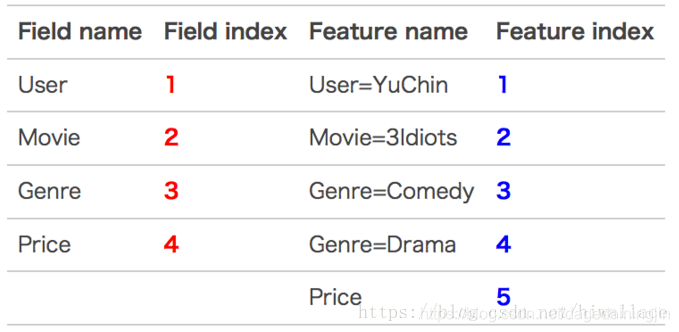
• 特征组合
  

DeepFM

FM通过对每一维特征的隐变量内积来提取特征组合，最后的结果也不错，虽然理论上FM可以对高阶特征组合进行建模，但实际上因为计算复杂度原因，一般都只用到了二阶特征组合。对于高阶特征组合来说，我们很自然想到多层神经网络DNN。

• FM结构
  
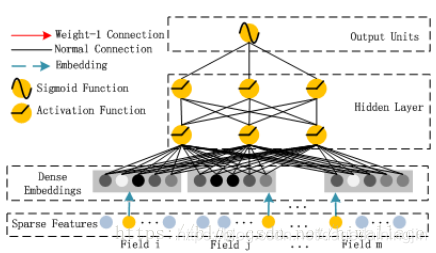
• DNN结构
  
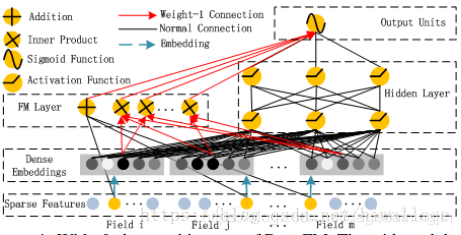
• DeepFM结构
  
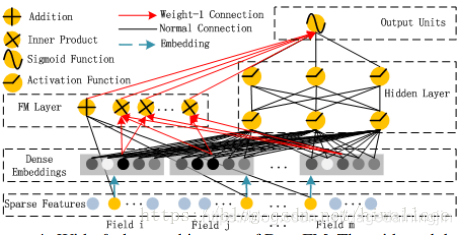
  DeepFM目的是同时学习低阶和高阶的特征交叉，主要由FM和DNN两部分组成，底部共享同样的输入。模型可以表示为：
  $\hat{y}=sigmoid(y_{FM}+y_{DNN})$
  Dense Embedding层在FM中理解为隐变量$V_i$，在DNN中理解为Embedding，解决数据过于稀疏问题
• DeepFM优势：
  1.DeepFM模型的Deep component和FM component从Embedding层共享数据输入，这样做的好处是Embedding层的隐向量在(残差反向传播)训练时可以同时接受到Deep component和FM component的信息，从而使Embedding层的信息表达更加准确而最终提升推荐效果。
  2.DeepFM模型同时对低阶特征组合和高阶特征组合建模，从而能够学习到各阶特征之间的组合关系
  3.DeepFM模型是一个端到端的模型，不需要任何的人工特征工程

参考：
1.https://blog.youkuaiyun.com/hiwallace/article/details/81333604
2.TensorFlow代码实现：https://blog.youkuaiyun.com/John_xyz/article/details/78933253