电磁直线执行器等效磁路设计

电磁直线执行器等效磁路方法

一、引言

直线执行器的设计变体通过应用液压动力以在长行程上获得大力而产生。然而，为了使其正常运行，液压驱动系统需要具备多个组件，例如液压泵、阀和连接软管。此外，通常难以实现连续力控制并获得快速响应时间。

电磁直线执行器已被提出以克服液压执行器的此类缺点。由于与液压或气动系统相比，其动态响应更好、精度更高、效率更高，因此在各个行业中正变得越来越受欢迎。此外，它们具有环保设计，能够保持工作区域清洁。因此，它们已广泛应用于发动机阀执行器、卡盘系统和快速振荡系统等众多领域 [1]

电磁直线执行器的一个应用是用作数控车床上的夹紧系统。它可替代液压旋转缸作为动力卡盘的驱动装置。一种可能的解决方案是将高力夹紧系统与线性运动装置结合，以在相对较长行程上产生小推力。尽管夹紧力的范围随卡盘尺寸而变化，但通常需要超过30千牛的高力，最高可达120千牛，以牢固夹持工件并承受高外部压力。同时，为产生如此大的力，对允许直径也存在限制。因此，将液压系统替换为电气系统具有很高的挑战性。为应对这些挑战，可考虑采用线圈激励型（COL）方法的线圈激励方法。该方法相比螺线管或多极螺线管（MPS） [6] 等其他线圈激励方法具有更高的力密度。先前的研究表明，当夹紧力被最大化时

磁通密度的大小和分布在线性定子极的气隙区域 [7] 是均匀的。然而，该方法需要对大量有限元进行分析，并且耗时较长，以分析槽和匝数对电感以及夹紧力的影响。

本研究利用等效磁路（EMC）方法分析了采用分体线圈激励系统的电磁直线执行器的设计变型。通过EMC方法获得各极中磁通的方向，并使用叠加原理计算各极的磁通密度。然后，为了使对应于定子极的气隙区域中的磁通密度均匀，采用了极迭代方法。与基于实验设计、根据分析数据寻找最优值的响应面法（RSM）[9],所得到的优化结果相比，所提出的方法表现出几乎相同的力特性。基于所提出的EMC方法，

通过改变槽宽和电流，研究了电磁直线执行器的特性。开发了一种直径为285毫米的电磁直线执行器，以产生35千牛的夹紧力，并将实验结果与分析结果进行了比较。

II. 直线执行器的分析

A. 直线执行器的结构和等效磁路模型

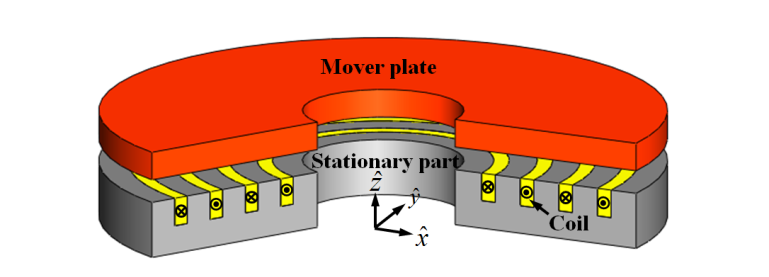
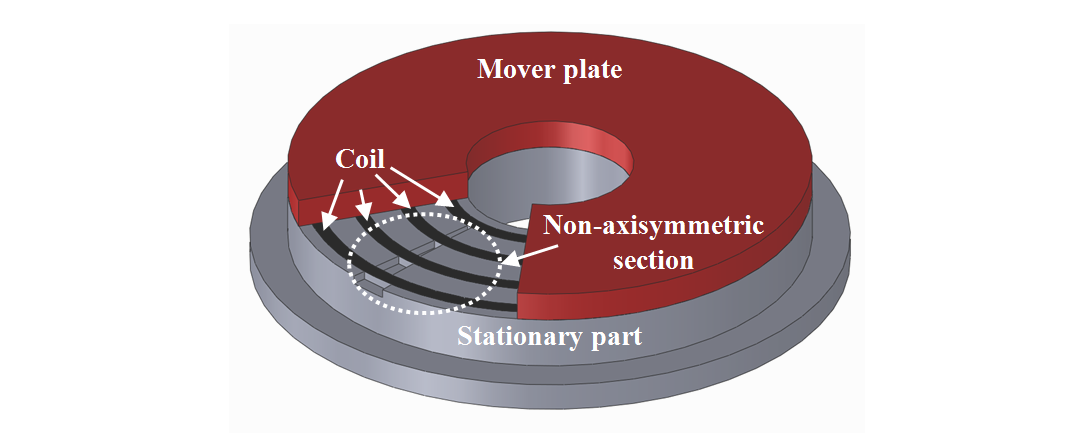
图1展示了采用COL激励的电磁直线执行器的三维视图。它由一个静止部分（其上线圈在相邻位置具有交替极性）和一个动板组成。如果所有线圈的磁动势（MMF）具有相同的极性方向，则称为MPS激励。图2显示了该电磁直线执行器的轴对称模型。气隙长度固定为0.1毫米，初始模型中所有槽和极的宽度相同。在这种情况下，气隙磁通密度分布不均匀，因此无法产生最大夹紧力。

设计变量	初始模型	RSM模型	EMC模型
极 1 (mm)	13.4	8.6	9.1
极 2 (mm)	13.4	16.7	17.1
极 3 (mm)	13.4	16.7	17.9
极 4 (mm)	13.4	16.7	16.0
极 5 (mm)	13.4	8.3	6.9

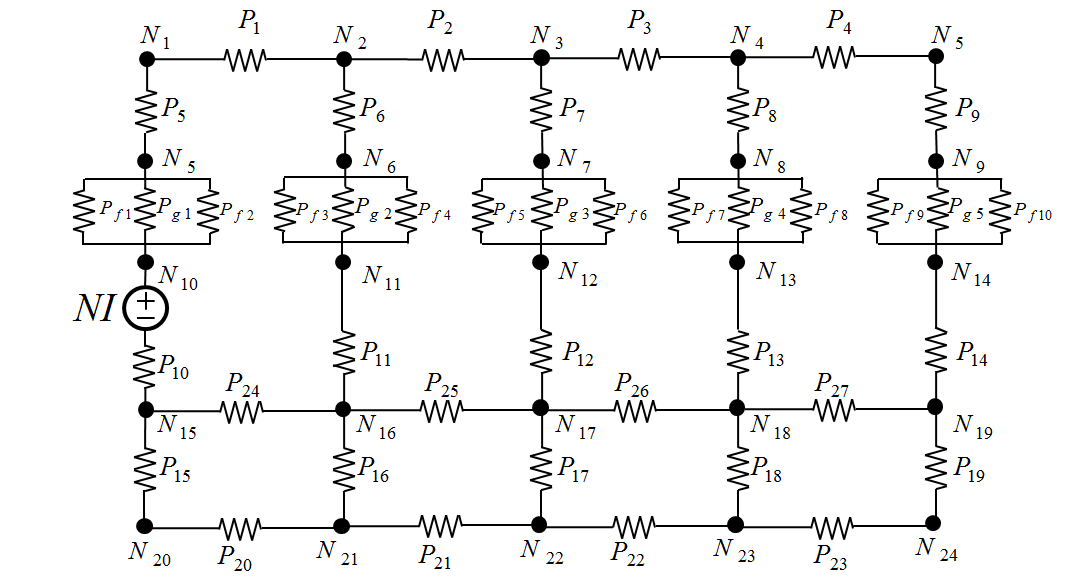
EMC模型在最内侧线圈被激励时的情况如图3所示。该模型包含极板磁导（P1~P9）、气隙磁导（Pg1~Pg5）、极身磁导（P10~P14）和轭部磁导（P15~P23）。此外，通过引入边缘磁导（Pf1~Pf10）和漏磁导（P24~P27），考虑了气隙处的边缘磁通和槽区的漏磁通。

B. EMC方法设计直线执行器

当槽数和极数确定后，应调整每极宽度以最大化夹紧力。首先，当一个线圈被激励时，各极中磁通的大小和方向可通过以下公式计算：

$$ {\phi} = [\mathcal{P}]^{-1} {F} $$

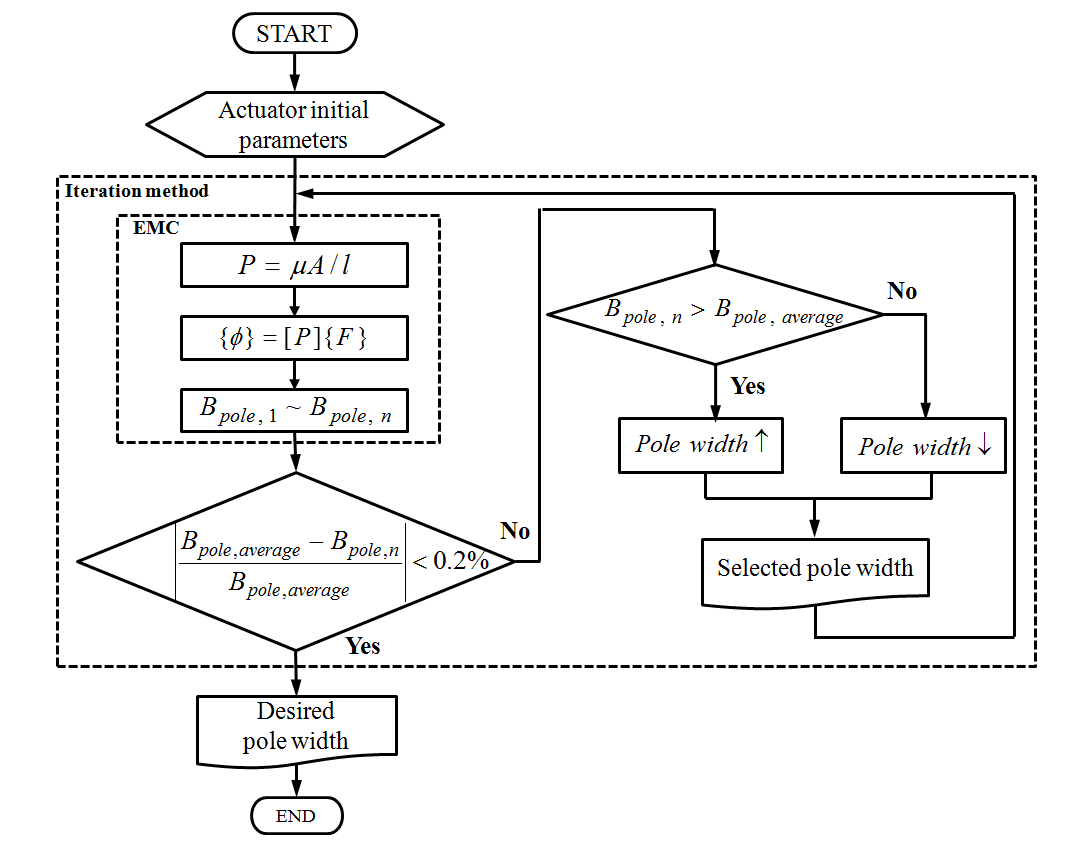
其中$[\mathcal{P}]$是由支路磁导组成的磁导矩阵，${\phi}$ 是表示各磁通流动极区的磁通矢量，${F}$ 是表示每个槽中施加的磁动势的激励矢量。每个极的总磁通密度（B _pole,n ，其中n为极数）可通过叠加每个线圈激励产生的磁通获得，极区的平均磁通密度（B _pole,average ）可根据B _pole,n 计算得到。为了使对应各极的气隙区域中的磁通密度均匀，应通过如图4所示的迭代方法调整极宽。如果B _pole,n 与B _pole,average 之间的绝对差值除以B _pole,average 大于容差值ε（在本例中为ε= 0.2%），则需调整极宽：当B _pole,n 大于B _pole,average 时，相应极宽增加；当B _pole,n 小于B _pole,average 时，相应极宽减小。若ε小于设定的容差值，则停止迭代，从而获得所需的极宽。通过线性分析，尽管磁通密度的绝对幅值与考虑非线性B‐H曲线的实际情况有所不同，但足以确定各个极宽以产生最大夹紧力。

在最终设计的极宽基础上，通过有限元模型上的虚功原理计算夹紧力。根据虚功法，在恒定电流下，磁共能$W_{co}$对位移z的导数即为z方向的力，如下所示：

$$ F = \left. \frac{\partial W_{co}}{\partial z} \right|_{i=\text{const}} $$

表I显示了当槽数为四时，响应面法和EMC方法下设计变量的值。图5(a)显示了初始模型（具有相同的极宽和槽宽）以及通过响应面法和EMC方法所提出的模型的气隙磁通密度分布曲线。与初始模型相比，采用EMC的优化模型在每个极上都具有均匀的气隙磁通密度分布，并且在每个磁动势区域中的力特性几乎与响应面法的结果相同，如图5(b)所示。

C. 随槽宽和电流变化的夹紧力与增量电感变化

基于电磁计算方法得到的结果，通过改变槽宽和输入电流来研究电磁直线执行器的夹紧力，如图6所示。在保持槽满率不变的情况下改变匝数。表II显示了槽宽变化时对应的匝数和电阻。正如预期的那样，由于极区相对增大，槽宽越小，夹紧力的线性区域越长。尽管槽宽为10毫米的模型在低输入电流时夹紧力上升最陡峭，但由于极区高度饱和，需要过大的输入电流才能达到35千牛的夹紧力。相比之下，当槽宽为8毫米时，与其他模型相比，可在最小输入电流下产生35千牛的夹紧力。当然，若考虑匝数因素，槽宽为5毫米时产生35千牛夹紧力所需的磁动势最小。

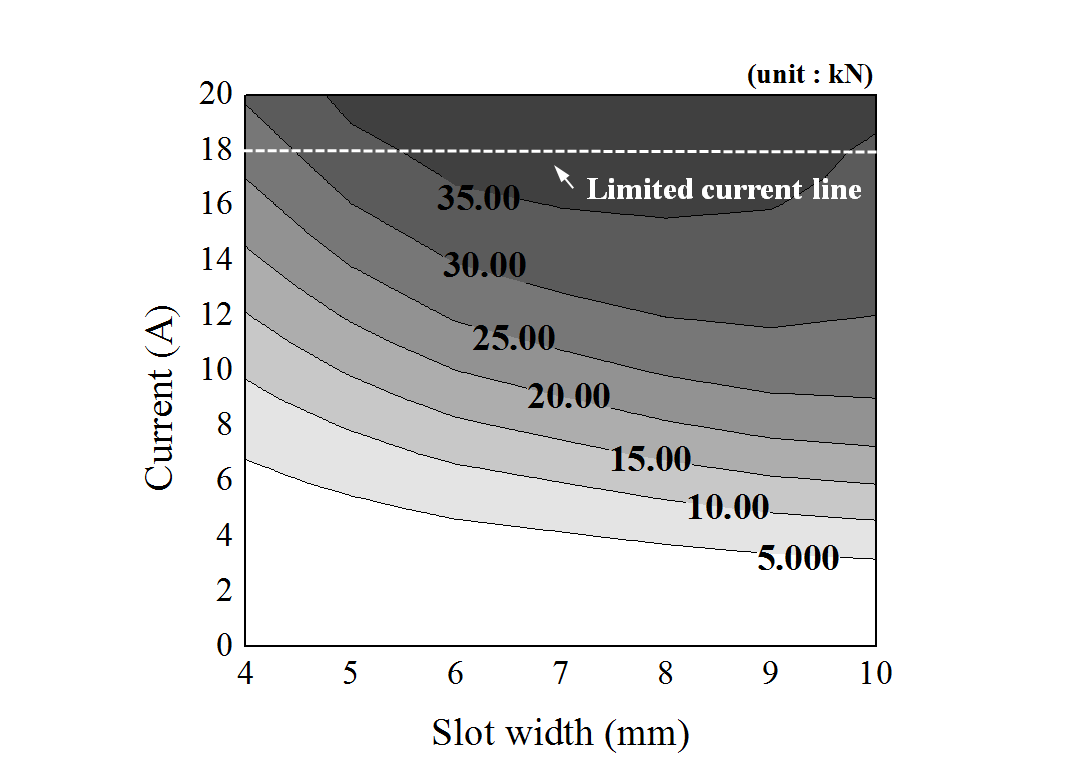
动态特性也非常重要，因为它决定了达到所需夹紧力的速度。在此系统中，电路的时间常数由增量电感与线圈电阻之比表示。图7显示了增量电感随输入电流和槽宽变化的情况。当输入电流较小时，具有较大槽宽的直线执行器的增量电感明显高于具有较小槽宽的直线执行器。这是由于大槽宽情况下施加的总磁动势增加所致。然而，随着电流增大，由于大槽宽下磁饱和程度的影响显著，情况发生逆转。图8显示了夹紧力随电流和槽宽变化的动态特性。考虑到电流密度，输入电流被限制在18安培。尽管具有较大槽宽的直线执行器的时间常数大于其他模型，但其夹紧力上升速度最快。然而，正如图6所预期的那样，槽宽为4毫米和10毫米的直线执行器在输入电流受限的情况下无法达到35千牛的夹紧力。

槽宽（毫米）	匝数	电阻 (Ω)
4	22	0.50
6	34	0.78
8	45	1.03
10	56	1.18
## III. 实验

开发了一种电磁直线执行器，用于产生35千牛的夹紧力，如图9所示。主要参数列于表III中，每极宽度由所提出的EMC方法确定。在开发COL激励方法时，每个线圈的输入输出端子应连接到电源。与图2所示的轴对称模型不同，所开发的模型具有非轴对称截面，需要进行三维分析以获得更好的结果，如图10所示。

图11通过实验和有限元分析对比了所开发直线执行器的夹紧力，包括轴对称二维模型和非轴对称三维模型。当输入电流较小时，夹紧力的实验结果小于分析模型的结果。这主要是由于制造过程中难以保持预定义的精度所致。然而，随着输入电流的增加，差异逐渐减小。分析结果与实验结果之间的差异减小，最终实验结果的夹紧力大于分析模型的结果。动板的弹性变形被认为是主要原因之一。随着输入电流的增加，动板受到较大的力，并向气隙区域弯曲，导致气隙长度减小。尽管由于制造变形，实验结果与非理想结果存在一定的差异，但产生的夹紧力可达40千牛。这表明所开发的直线执行器有可能用于卡盘系统中牢固地夹持工件和气缸。

参数	值	参数	值
槽宽	8 mm	极宽1	18 mm
槽高	17 mm	极宽2	19 mm
线圈直径	1.5 mm	极宽3	17 mm
槽数	4	极宽4	7 mm
匝数	45	极宽5	——

IV. 结论

本文提出了一种用于夹紧装置的直线执行器设计，该设计在定子气隙区域磁通密度的大小和分布均匀时，使COL激励最大化。通过电磁计算（EMC）和迭代方法调节每极宽度，所得结果与基于有限元分析的响应面法（RSM）几乎一致。通过改变槽宽和输入电流，研究了电磁直线执行器的夹紧力和电感。基于所提出的方法，开发了一种可产生35千牛夹紧力的电磁直线执行器，实验结果表明，该执行器可在卡盘系统中替代液压缸，实现对工件的可靠夹紧。