C++：递归与分治策略--逆序计数

① 问题描述（Problem Description）

给定一个整数序列 S=[a1,a2,…,an]，
要求计算其中“逆序对”的数量。

若存在 i<j且 ai>aj，
则称 (ai,aj)为一个逆序对。

例如：

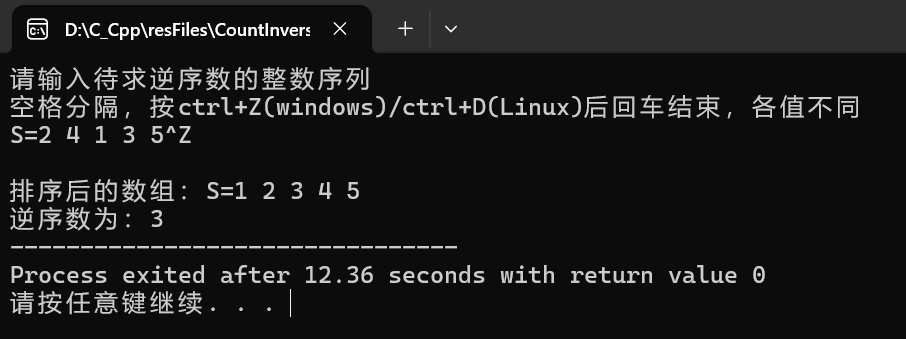
S = [2, 4, 1, 3, 5]
逆序对为：(2,1), (4,1), (4,3)
共3个。

② 算法思想（Design Idea）

使用 分治法（Divide and Conquer）：

1. 将数组平均分为左右两半。

2. 递归地分别计算左右部分的逆序对数。

3. 在合并（归并）时，再统计跨左右的逆序对。

💡 关键思想：
当左半部分和右半部分已排好序后，
如果左边的元素 A[i] > 右边的元素 B[j]，
则 A[i] 及其之后的所有元素都与 B[j] 形成逆序。

③ 流程图（Flowchart）

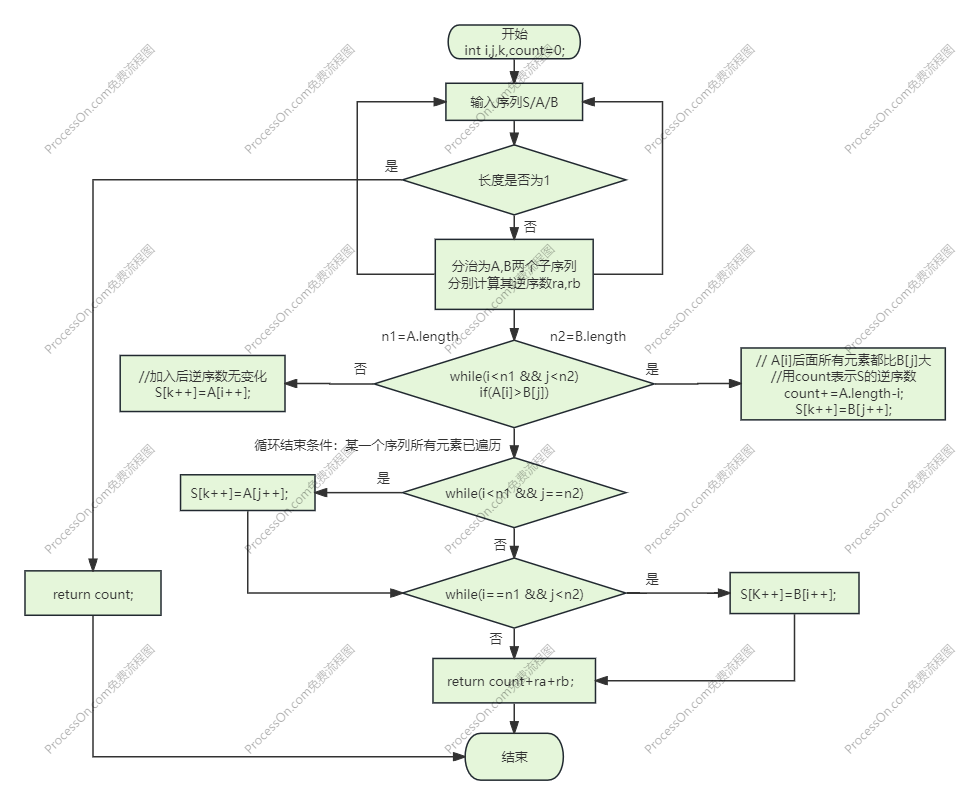
④ 伪代码（Pseudocode）

Algorithm CountInversions(S)
Input: 数组 S[1..n]
Output: 逆序对数量 count

if n == 1 then
    return 0
split S into A and B
rA ← CountInversions(A)
rB ← CountInversions(B)
(r, S_sorted) ← MergeAndCount(A, B)
return rA + rB + r

Algorithm MergeAndCount(A, B)
Input: 已排序的A、B
Output: 合并后序列C和逆序数count

i ← 0, j ← 0, count ← 0
C ← []
while i < len(A) and j < len(B):
    if A[i] ≤ B[j]:
        append A[i] to C
        i ← i + 1
    else:
        append B[j] to C
        count ← count + (len(A) - i)
        j ← j + 1
append remaining A and B to C
return (count, C)

⑤ 正确性分析

递归终止条件保证单元素序列逆序数为0；
每层合并统计保证所有跨左右区间的逆序都被精确计入。
因此算法能正确计算所有逆序对。

⑥ 时间复杂度分析

递推关系：

        T(n)=2T(n/2)+O(n)

根据主定理：

        T(n)=O(nlog⁡n)

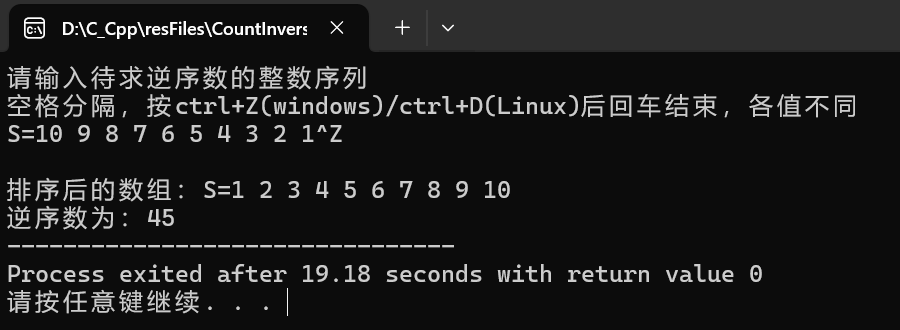
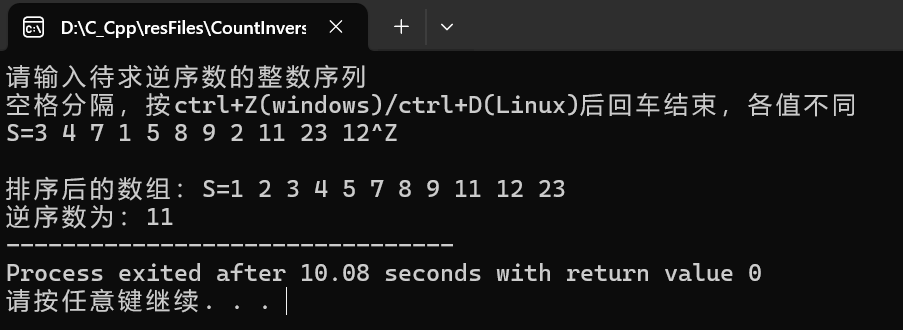
⑦ 实验结果与结论

• 普通算法：O(n²)

• 分治算法：O(n log n)

• 当 n 较大时，性能提升显著。

• 算法本质是“归并排序 + 计数”。

⑧ 源代码

已在Dev C++中测试过以下代码

#include <iostream>
#include <vector>
using namespace std;

long long MergeAndCount(vector<int>& S,int left,int mid,int right){
	int n1 = mid - left + 1;// 序列A的长度
	int n2 = right - (mid + 1) +1;// 序列B的长度：n2 = right - mid 
	
	vector<int> A(n1),B(n2);
	for(int i=0;i<n1;i++) A[i] = S[left+i];// A为S的左半部分 
	for(int j=0;j<n2;j++) B[j] = S[mid+1+j];// B为S的右半部分
	
	int i=0,j=0,k=left;// left为待求序列起始位置的下标 
	long long count=0;// 累计逆序数 
	
	while(i<n1 && j<n2){
		if(A[i]>B[j]){
			count += (n1 - i);// 如果A[i]>B[j]，则A[i+1]...都比B[j]大 
			S[k++] = B[j++];// 存入较小数 
		}else{
			S[k++] = A[i++];// 存入较小数 
		}
	} 
	
	while(i<n1 && j==n2) S[k++] = A[i++];// 如果A还有剩余元素而B元素全部遍历，则存入 
	while(i==n1 && j<n2) S[k++] = B[j++];// 如果A元素全部遍历而B还有剩余元素，则存入 
	
	return count;
}

long long CountInversions(vector<int>& S,int left,int right){
	long long count = 0;// 逆序数初始值赋为0 
	if(left<right){// 如果序列长度不为1 
		int mid = left + (right-left)/2;// 划分为左右两部分子序列 
		
		count += CountInversions(S,left,mid);// A序列 
		count += CountInversions(S,mid+1,right);// B序列 
		count += MergeAndCount(S,left,mid,right);// A、B有序序列合并 
	}
	return count;// 返回逆序数 
}

int main(){
	ios::sync_with_stdio(false);// 禁用同步I/O 
    
    cout<<"请输入待求逆序数的整数序列"<<endl<<"空格分隔，按ctrl+Z(windows)/ctrl+D(Linux)后回车结束，各值不同"<<endl<<"S=";// 输入序列S 
	vector<int> S;
	int num;
	while(cin>>num) S.push_back(num);
	
	long long inversions = CountInversions(S,0,S.size()-1); // 计算逆序数 
	
	cout<<"\n排序后的数组：S=";// 输出结果 
	for(int i=0;i<S.size();i++) {
		cout<<S[i]<<" ";
	}
	cout<<"\n逆序数为："<<inversions;
	
	return 0;
}