吴恩达机器学习笔记（一）

1 Introduction

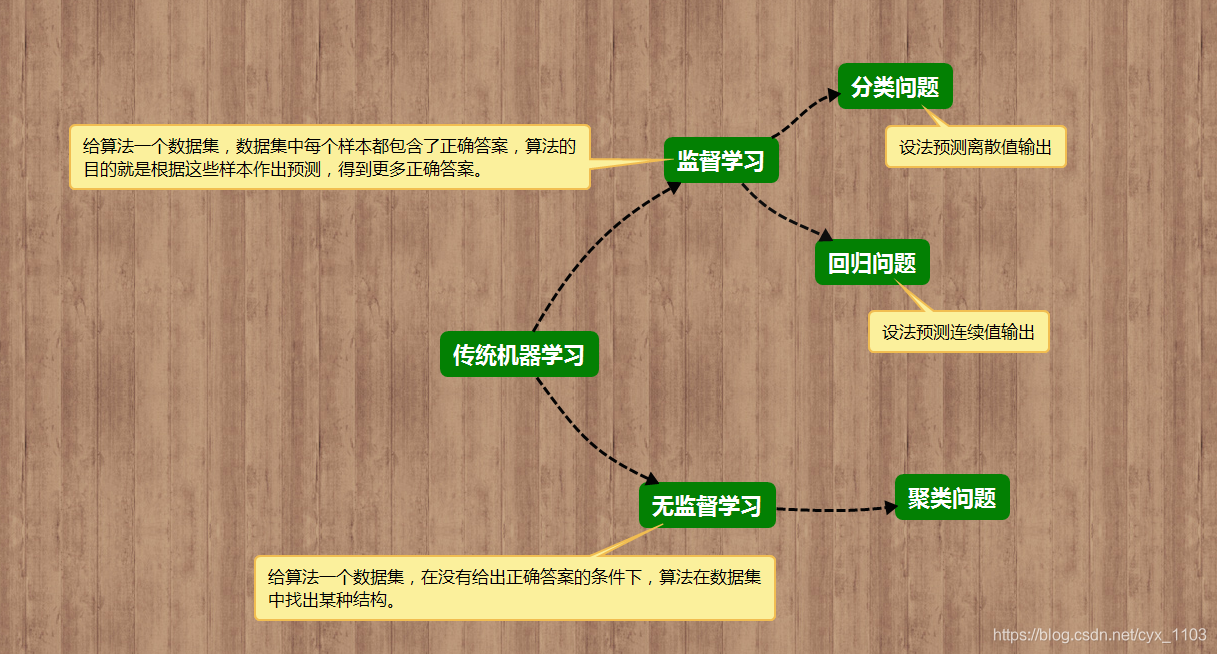
什么是机器学习

1、Arthur Samuel的定义：在没有明确设置的情况下，使计算机具有学习能力的研究领域。

2、Tom Mitchell的定义：计算机程序从经验E中学习，解决某一任务T进行某一性能度量P，通过P测定在T上的变现因经验E而提高。

2 Linear Regression with One Variable（单变量线性回归）

2.1 model representation（模型表示）

这是课程中涉及到的第一个算法：线性回归算法

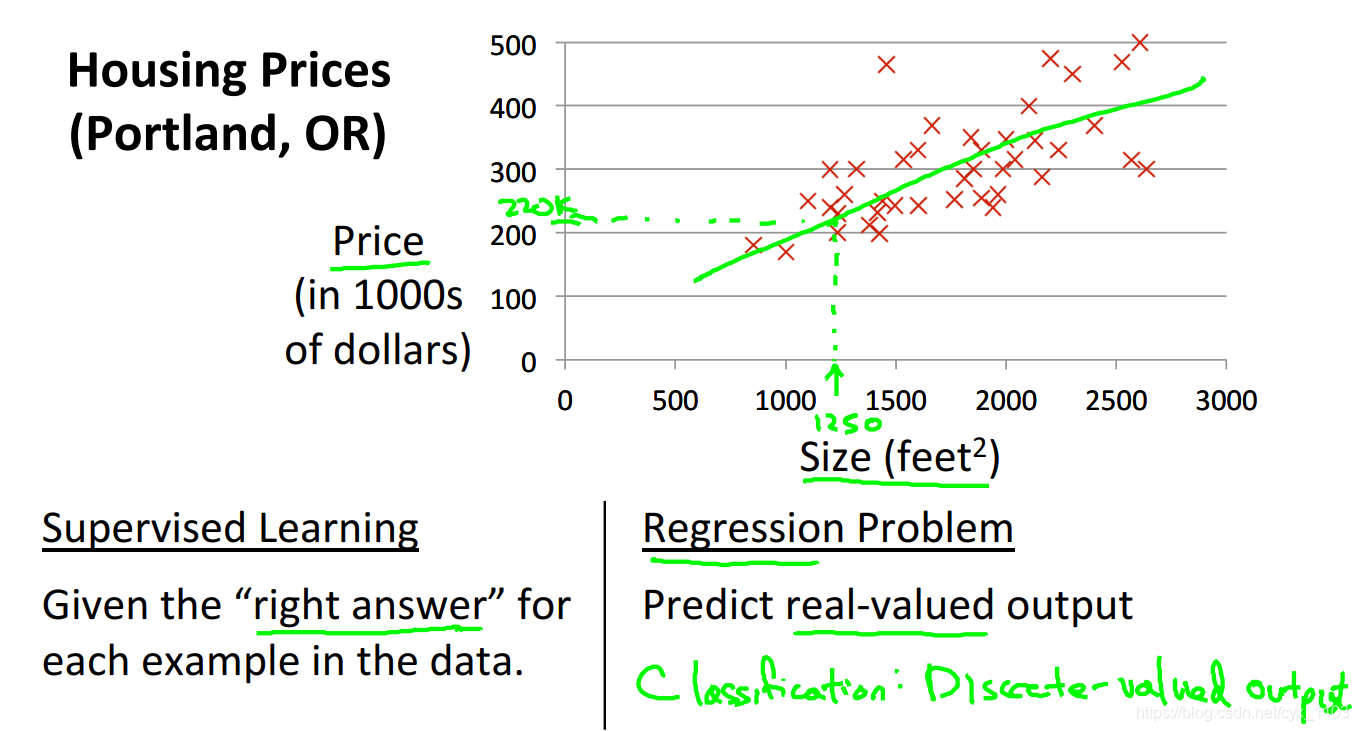
如上图所示，我们用一条直线来拟合预测函数，因为要预测的是房子的价格，输出一个连续值，因此是回归问题。

就这个房屋价格预测问题，我们用一些变量来描述解决方案：
$m$：训练集中样本的数量
$x$：输入的变量/样本特征
$y$：输出的目标变量/结果

$\left(x^{(i)},y^{(i)}\right)$：第i个样本

$h_{\theta }(x)$：学习算法的解决方案或函数 ，一般的解决方案都用$h$标记

一般的学习流程如下图：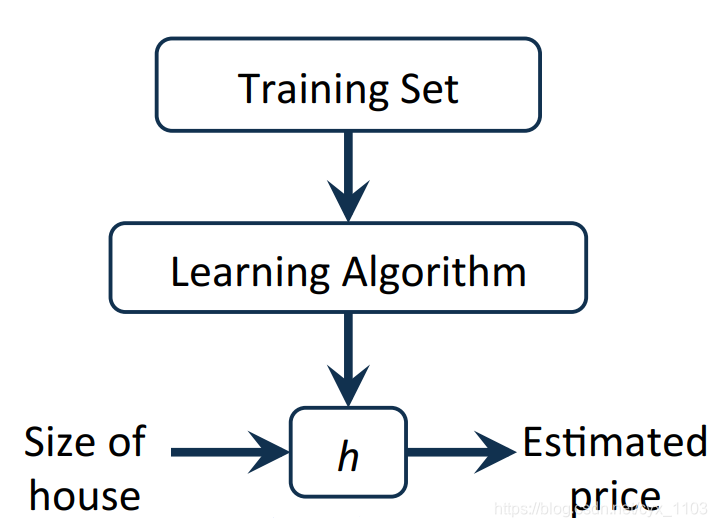

可以看到，输入训练集，经过学习算法得到预测函数h，再用h根据输入的特征预测输出。

对于房屋价格预测这个问题，我们假设函数h为线性函数，并且$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$，可以看到预测函数h只含有一个特征/输入变量，因此我们将这样的问题叫作单变量线性回归问题 。

2.2 cost function（代价函数）

由上一节，我们得到了线性回归算法的一个简单的数学模型，那么我们怎么选择这个模型的参数才能让我们得到的模型能最靠近正确的结果？由此引进了代价函数。我们知道，就上面的房屋价格预测问题，最好的结果是模型正好经过全部的点，但是显然用线性回归模型是做不到的，那么我们只能让直线离所有的点越近越好，也就是模型所预测的值与训练集中实际值之间的差距越小越好，这个差距如下面的图所示，也称为建模误差。

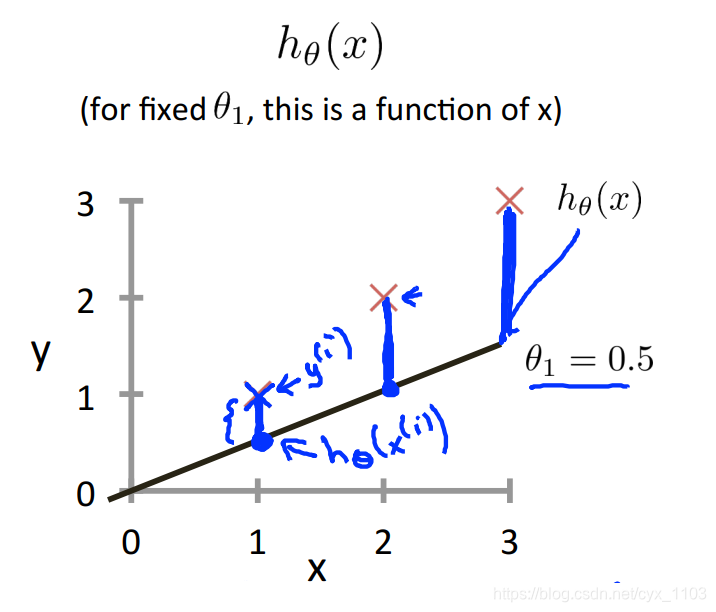
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数， 即使得代价函数 $J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$的值最小。

整理一下，整个问题归结为以下的问题：

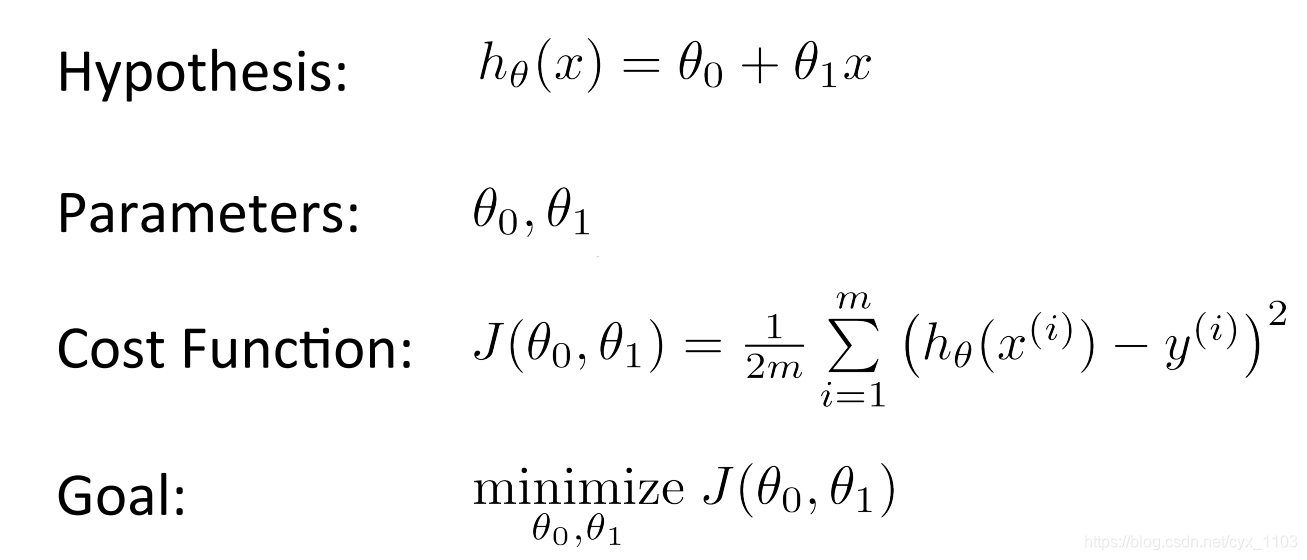
目标是找出让代价函数最小的参数的值，由此得到预测函数。我们可以画出代价函数在直角坐标空间中的图像，如下图所示：

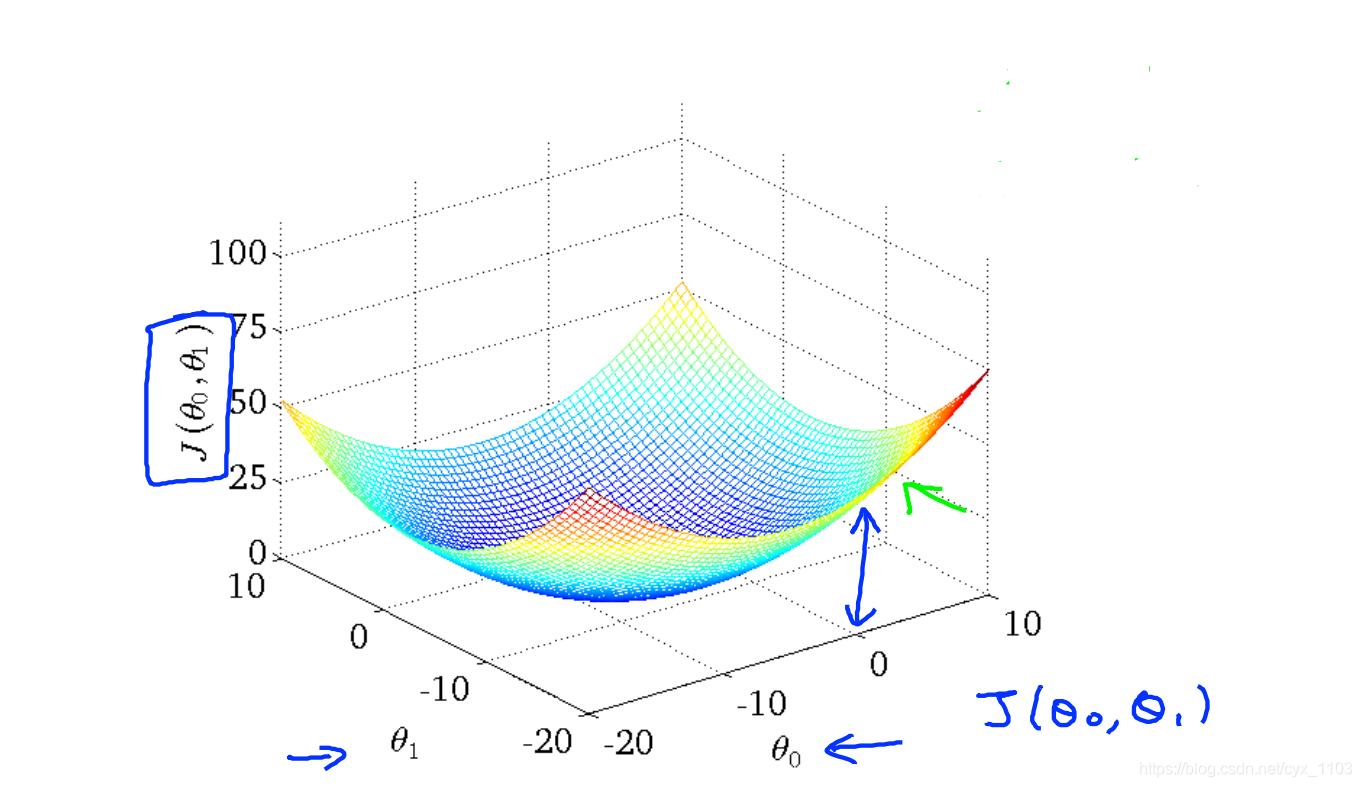
可以看出的是，空间中存在让代价函数最小的点。代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。

2.3 Gradient Descent （梯度下降）

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J\left({\theta }_0,{\theta }_1\right)$的最小值。

梯度下降背后的思想是：开始时我们随机选择一个参数的组合$\left({\theta }_0,{\theta }_1,\dots \dots ,{\theta }_n\right)$，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值，因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值，选择不同的初始参数组合，可能会找到不同的局部最小值 ，如下面两幅图所示。

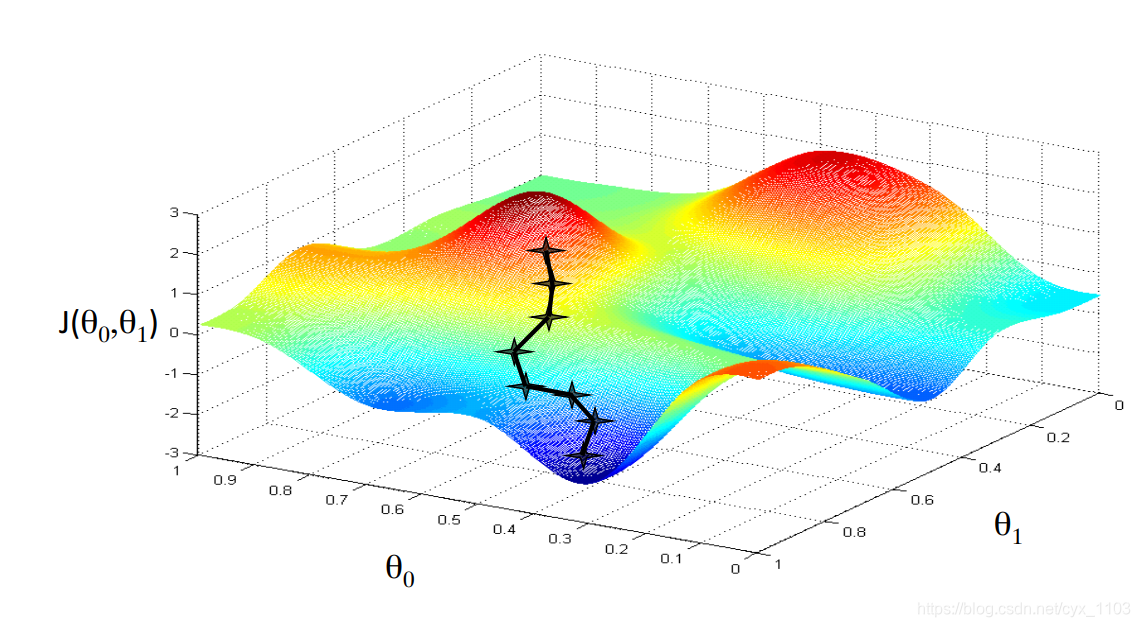
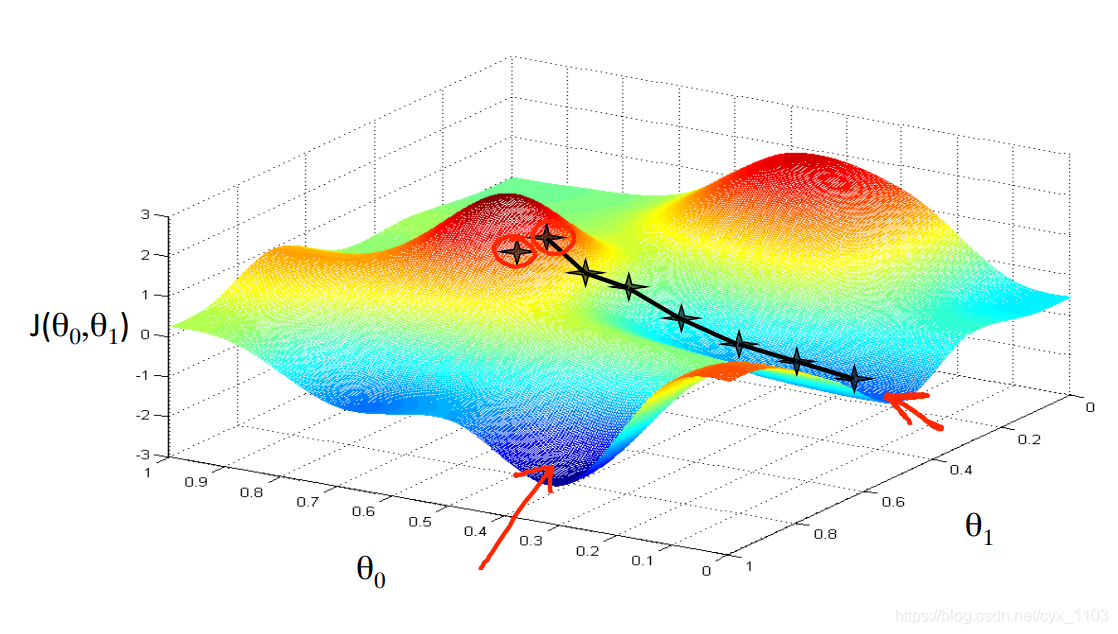
批量梯度下降算法的公式为：

repeat until convergence {\{{
${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J\left({\theta }_0,{\theta }_1\right)$ (simultaneously update，$j=0$ and $j=1)$

$\}$

其中$\alpha$是学习率，它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

如果$\alpha$太小了，即学习速率太小，那么每次只能挪动一点去努力接近最低点，这样就需要很多步才能到达最低点。而如果$\alpha$太大了，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远。

在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。

在更新${\theta }_0和{\theta }_1$时，我们要同时更新两个参数。如果我们初始化参数组合在局部最低点，由于该点的导数为0，${\theta }_0,{\theta }_1$的值将不变，也就是收敛到局部最低点了。

2.4 Gradient descent for linear regression（梯度下降的线性回归）

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：

$$\frac{\partial }{\partial {\theta }_j}J\left({\theta }_0,{\theta }_1\right)=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$

$j=0:\frac{\partial }{\partial {\theta }_0}J\left({\theta }_0,{\theta }_1\right)=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)$

$j=1:\frac{\partial }{\partial {\theta }_1}J\left({\theta }_0,{\theta }_1\right)=\frac{1}{m}{\sum }_{i=1}^m\left(\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\cdot x^{(i)}\right)$

则算法改写成：

Repeat {\{{
${\theta }_0:={\theta }_0-a\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)$
${\theta }_1:={\theta }_1-a\frac{1}{m}{\sum }_{i=1}^m\left(\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)\cdot x^{(i)}\right)$
$\}$

最终结果就是得到收敛后的参数组合，得到预测函数$h_{\theta }(x)$。