leetCode313超级丑数（动态规划）

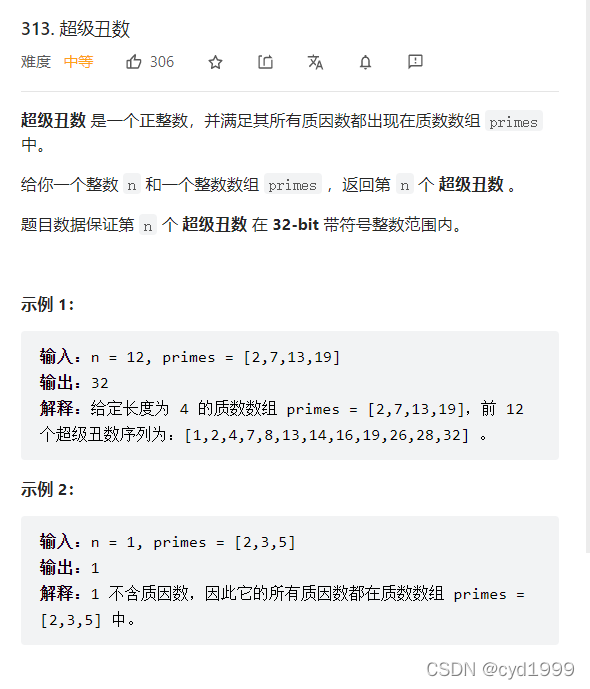
请看题

根据题目的意思我们很容易发现。每一个新的丑数都是等于前面的某个丑数乘以对应的质因子得到的。这就是状态转移的过程，仔细想想，我们该怎样才能知道是用前面哪个丑数乘以哪个质因子呢。
先用一个例子分析一下：质因子为primers = [2,3,17,19]，

1. 第一个丑数f(0) = 1,
2. 第二个丑数:f(1) = min(f(0)*primers[0]…primerrs[3])=2。第二个丑数用到的是f(0)乘以第一个因子得到f(1)。
3. 所以第三个丑数f(2) = min(f(0)*primers[1], f(0)*primers[2], 4. f(1)*primers[0]) = f(0)*primers[1] = 3,
4. 所以第四个丑数为:f(3) = min(f(1)*primers[1], f(0)*primers[2], f(1)*primers[0]) = f(1)*primers[0] = 4

综上我们可以发现，我们只需要维护一个primers.size()长度的指针序列，每个指针指向相应的质因子转移到的上一个丑数状态即可，再用一个数组维护待选丑数即可

代码如下

class Solution {
public:

    
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n == 1){
            return 1;
        }
        int m = primes.size();
        vector<int> points(m, 0);//指针数组
        vector<long long> nums(primes.begin(), primes.end());
        vector<long long> dp;
        dp.push_back(1);
        while (dp.size() < n)
        {
            long long minNum = INT64_MAX;
            for(int i=0;i<m;i++){
                minNum = min(nums[i], minNum);
            }
            dp.push_back(minNum);
            for(int i=0;i<m;i++){
                if(nums[i]==minNum){
                    points[i]++;
                    nums[i] = dp[points[i]]*primes[i];
                }
            }
        }
        return dp.back();
    }
};

用一个优先队列对待选值优化一下可得

class Solution {
public:

    
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n == 1){
            return 1;
        }
        int m = primes.size();
        
        priority_queue<pair<long long, pair<int, int>>, vector<pair<long long, pair<int, int>>>, greater<pair<long long, pair<int, int>>>> qu;
        for(int i=0;i<primes.size();i++){
            qu.push(make_pair(primes[i], make_pair(0, i)));
        }
        vector<long long> dp;
        dp.push_back(1);
        while (dp.size() < n)
        {
            long long minNum = qu.top().first;
            dp.push_back(minNum);
            while(qu.top().first == minNum){
                auto e = qu.top();
                qu.pop();
                e.second.first++;
                e.first = primes[e.second.second]*dp[e.second.first];
                qu.push(e);
            }
        }
        return dp.back();
    }
};

当然以上代码是我看了题解之后写的，刚开始我想到的是对前面每一个状态维护一个待选值。然后利用优先队列找出当前丑数，但是最后超时了。。。
代码如下

class Solution {
public:
    struct node
    {
        int xi;
        int yi;
        node(){}
        node(int x, int y){
            xi = x;
            yi = y;
        }
        friend bool operator <(const node &o1, const node &o2){
            return o1.xi<o2.yi;
        }

    };
    
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n == 1){
            return 1;
        }
        int m = primes.size();
        priority_queue<pair<int, node>, vector<pair<int, node>>, greater<pair<int, node>>> qu;
        qu.push(make_pair(primes[0], node(1, 0)));

        int val = 1, cnt = 1;
        
        while(cnt<n){
            cout<<val<<" ";
            pair<int, node> top = qu.top();
            qu.pop();
            if(top.second.yi<m-1)
                qu.push(make_pair(top.second.xi*primes[top.second.yi+1], node(top.second.xi, top.second.yi+1)));
            
            if(top.first!=val){
                qu.push(make_pair(top.first*primes[0], node(top.first,0)));
                val = top.first;
                cnt++;
            }

        }
        return val;
    }
};

原因我分析了一下，就是我维护的这些状态好多都是当下没用的，比如前面有一个丑数f(k)，维护的待选值是f(i)*primers[0], 后面有一个丑数f(k+3),也维护了一个待选值f(k+3)*primers[0]，很明显，后面的丑数是没必要的，因为我们要选择当下维护的丑数里面最小的，当primer[0]确定时，f(k+3)*primers[0]肯定时多余的，也就是说一个primer[i]对应的只需要维护一个丑数即可，再选中之后再转移到下一个丑数即可。