<think>我们正在讨论两个向量的距离计算方法。根据引用[1]和[3]，常见的向量距离计算方法包括曼哈顿距离和欧几里得距离。引用[2]给出了欧几里得距离的具体代码实现。此外，引用[3]还提到了余弦相似度、Jaccard距离和编辑距离等，但注意编辑距离通常用于字符串，而余弦相似度衡量的是方向相似性而非距离（但可通过转换得到距离度量）。
接下来，我将详细介绍几种常用的向量距离计算方法：
1. **欧几里得距离（Euclidean Distance）**
这是最常用的距离度量方法，表示两点之间的直线距离。对于两个n维向量$I_i=(I_{i1}, I_{i2}, ..., I_{in})$和$I_j=(I_{j1}, I_{j2}, ..., I_{jn})$，其计算公式为：
$$ d(I_i, I_j) = \sqrt{\sum_{k=1}^n (I_{ik} - I_{jk})^2} $$
在二维情况下，即用户提供的代码中使用的距离计算方法（引用[2]）：
```cpp
double dx = p1.pose.position.x - p2.pose.position.x;
double dy = p1.pose.position.y - p2.pose.position.y;
return sqrt(dx * dx + dy * dy);
```
2. **曼哈顿距离（Manhattan Distance）**
也称为城市街区距离，是各维度差值的绝对值之和。计算公式为（引用[1]）：
$$ d_1(I_i, I_j) = \sum_{k=1}^n |I_{ik} - I_{jk}| $$
3. **余弦相似度（Cosine Similarity）**
虽然余弦相似度衡量的是两个向量方向的相似性（值域为[-1,1]），但可以通过转换得到距离度量。余弦相似度定义为：
$$ \text{cosine\_similarity}(I_i, I_j) = \frac{I_i \cdot I_j}{\|I_i\| \cdot \|I_j\|} $$
对应的余弦距离通常定义为：$1 - \text{cosine\_similarity}(I_i, I_j)$，值域为[0,2]。
4. **切比雪夫距离（Chebyshev Distance）**
各维度差值的绝对值的最大值：
$$ d_{\infty}(I_i, I_j) = \max_{k} |I_{ik} - I_{jk}| $$
5. **闵可夫斯基距离（Minkowski Distance）**
这是欧几里得距离和曼哈顿距离的推广，定义如下：
$$ d_p(I_i, I_j) = \left( \sum_{k=1}^n |I_{ik} - I_{jk}|^p \right)^{1/p} $$
当$p=1$时，为曼哈顿距离；当$p=2$时，为欧几里得距离；当$p \to \infty$时，为切比雪夫距离。
6. **汉明距离（Hamming Distance）**
用于比较两个等长字符串（或向量）在相同位置上不同字符（或元素）的个数。例如，向量(1,0,1)和(1,1,1)的汉明距离为1。
7. **杰卡德距离（Jaccard Distance）**
用于衡量两个集合的差异程度。对于两个集合A和B，杰卡德相似系数为$J(A,B)=\frac{|A \cap B|}{|A \cup B|}$，杰卡德距离则定义为$1-J(A,B)$。
8. **编辑距离（Edit Distance）**
主要用于字符串，表示将一个字符串转换成另一个字符串所需的最少编辑操作次数（插入、删除、替换）。
注意：在选择距离度量时，需要根据具体问题和数据特性来确定。例如，欧几里得距离对量纲敏感，因此在使用前通常需要标准化数据。
下面我们用一个简单的例子来演示几种距离的计算。假设有两个二维向量A=(1,3)和B=(4,7)：
- 欧几里得距离：$\sqrt{(1-4)^2 + (3-7)^2} = \sqrt{9+16} = 5$
- 曼哈顿距离：$|1-4| + |3-7| = 3+4 = 7$
- 切比雪夫距离：$\max(|1-4|, |3-7|) = \max(3,4)=4$
- 余弦相似度：$\frac{1\cdot4 + 3\cdot7}{\sqrt{1^2+3^2}\cdot\sqrt{4^2+7^2}} = \frac{25}{\sqrt{10}\cdot\sqrt{65}} \approx 0.98$，余弦距离约为0.02
在实际应用中，我们通常根据问题的性质选择合适的距离度量。例如：
- 在机器学习中，k-NN算法默认使用欧几里得距离，但也可以根据特征的性质选择其他距离度量。
- 文本相似度计算中，常用余弦相似度或杰卡德距离。
- 图像处理中，对于像素位置的距离可能使用曼哈顿距离（如棋盘上的移动）。
总结：向量距离的计算方法多种多样，选择合适的方法取决于具体应用场景和数据特性。
</think>### 向量距离计算方法详解
在数学和计算机科学中，计算两个向量间的距离是基础操作，主要方法如下：
#### 1. **欧几里得距离（Euclidean Distance）**
最常用的距离度量方法，表示两点间的直线距离。给定两个n维向量$\vec{a}=(a_1,a_2,...,a_n)$和$\vec{b}=(b_1,b_2,...,b_n)$，计算公式为：
$$ d(\vec{a},\vec{b}) = \sqrt{\sum_{i=1}^n (a_i - b_i)^2} $$
例如二维平面中：
$$ d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} $$
代码实现如引用[2]所示，常用于空间坐标计算[^2]。
#### 2. **曼哈顿距离（Manhattan Distance）**
又称城市街区距离，计算各维度绝对差之和：
$$ d_1(\vec{a},\vec{b}) = \sum_{i=1}^n |a_i - b_i| $$
适用于网格状路径规划（如棋盘移动）[^1]。
#### 3. **余弦相似度（Cosine Similarity）**
衡量向量方向的相似性：
$$ \text{cos}(\theta) = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \cdot ||\vec{b}||} $$
其中$||\vec{a}||$是模长：
$$ ||\vec{a}|| = \sqrt{\sum_{i=1}^n a_i^2} $$
广泛用于文本相似度计算[^3]。
#### 4. **闵可夫斯基距离（Minkowski Distance）**
泛化的距离公式：
$$ d_p(\vec{a},\vec{b}) = \left( \sum_{i=1}^n |a_i - b_i|^p \right)^{1/p} $$
当$p=1$时为曼哈顿距离，$p=2$时为欧氏距离。
#### 5. **汉明距离（Hamming Distance）**
适用于离散向量（如二进制串）：
$$ d_h = \text{不同位置的数量} $$
例如$(1,0,1)$和$(1,1,1)$的汉明距离为1。
---
### 选择指南
| **距离类型** | **适用场景** | **特性** |
|---------------------|----------------------------------|------------------------------|
| 欧几里得距离 | 空间坐标、物理测量 | 旋转不变性 |
| 曼哈顿距离 | 网格路径、图像处理 | 计算效率高 |
| 余弦相似度 | 文本分析、推荐系统 | 忽略向量长度，专注方向 |
| 汉明距离 | 编码校验、DNA序列比对 | 仅适用于离散数据 |
> 关键原则：高维数据中欧氏距离易受维度灾难影响，此时余弦相似度或标准化欧氏距离更优[^3]。
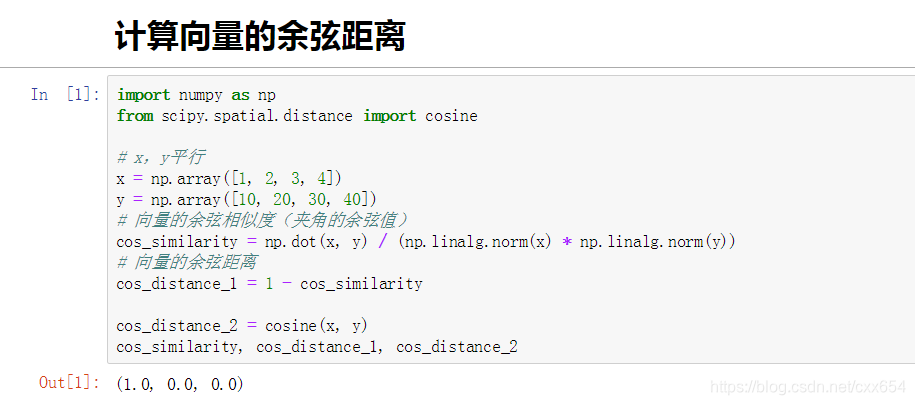
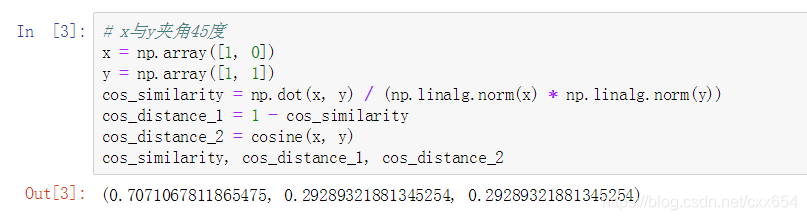
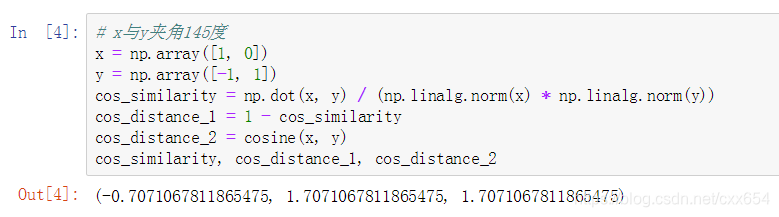
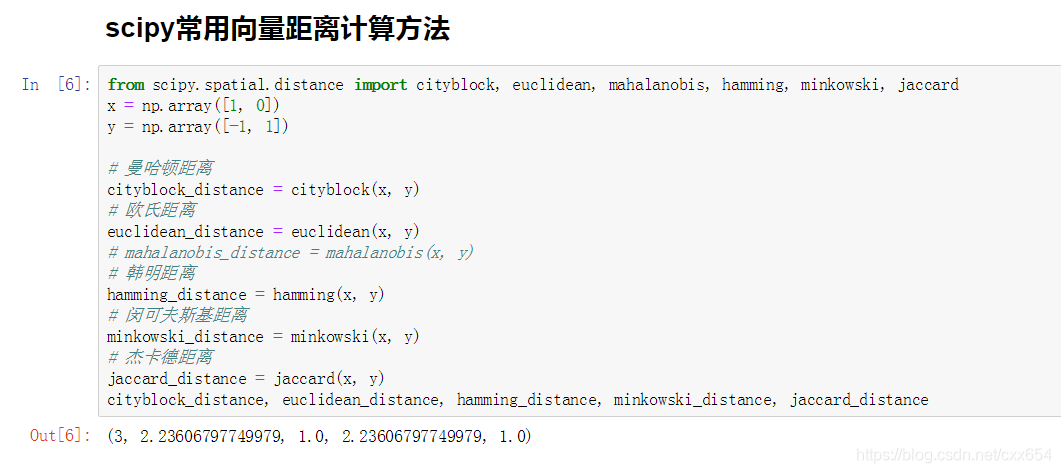
本文介绍了几种常用的向量空间距离计算方法，包括欧式距离、余弦距离和相似度、曼哈顿距离等，并演示了如何使用scipy和sklearn库进行实际计算。
扫一扫
10万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
