pytorch实现多项式拟合

最新推荐文章于 2025-06-12 14:46:29 发布

The_Matrix_

最新推荐文章于 2025-06-12 14:46:29 发布

阅读量3.2k

点赞数 2

CC 4.0 BY-SA版权

分类专栏： Pytorch

本文链接：https://blog.youkuaiyun.com/cuixing001/article/details/82317630

Pytorch 专栏收录该内容

2 篇文章

订阅专栏

本文介绍了一个使用PyTorch实现的多项式拟合案例，通过定义多项式的真值系数，生成数据样本，并利用神经网络模型来逼近这个多项式函数。该过程包括模型训练、损失计算与参数更新等步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先给出真值多项式参考方程：

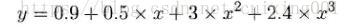
其对应参数形式为：

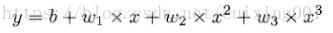
程序实现思路为：根据方程1，给定一些列（假如默认是32个）（x，y）对应点集，及最小均方差为目标，求解最佳参数（w1,w2,w3,b）。

终止条件：小于1e-3退出循环。

编辑器：Spyder

# -*- coding: utf-8 -*-
"""
Created on Sun Sep  2 17:54:11 2018

@author: Cuixingxing
"""

import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.optim as optim

#%% w和b系数矩阵，注意返回的是N*3大小矩阵
def make_features(x): 
 x = x.unsqueeze(1) 
 return torch.cat([x ** i for i in range(1,4)] , 1)

#%% 要拟合的多项式真值系数w和b
W_target = torch.FloatTensor([0.5,3,2.4]).unsqueeze(1)
b_target = torch.FloatTensor([0.9])

def f(x):
    return x.mm(W_target)+b_target[0]

def get_batch(batch_size=32): 
 random = torch.randn(batch_size) 
 x = make_features(random) 
 '''Compute the actual results'''
 y = f(x) 
 if torch.cuda.is_available(): 
  return Variable(x).cuda(), Variable(y).cuda() 
 else: 
  return Variable(x), Variable(y)

class poly_model(nn.Module): 
 def __init__(self): 
  super(poly_model, self).__init__() 
  self.poly = nn.Linear(3,1) 
  
 def forward(self, x): 
  out = self.poly(x) 
  return out 

if torch.cuda.is_available(): 
 model = poly_model().cuda() 
else: 
 model = poly_model() 

criterion = nn.MSELoss() 
optimizer = optim.SGD(model.parameters(), lr = 1e-3)

epoch = 0
while True: 
 batch_x,batch_y = get_batch() 
 output = model(batch_x) 
 loss = criterion(output,batch_y) 
 print_loss = loss.item() 
 optimizer.zero_grad() 
 loss.backward() 
 print("loss:%.5f\n" % loss)
 optimizer.step() 
 epoch+=1
 if print_loss < 1e-3: 
  break

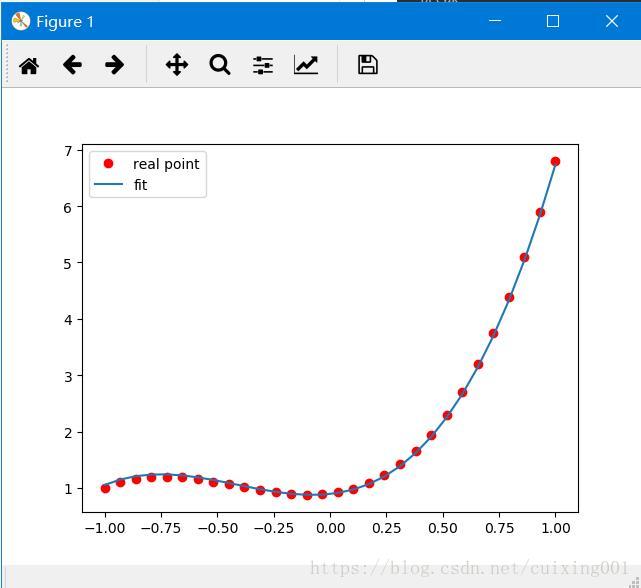
#%% 绘制真值和拟合结果曲线
x = np.linspace(-1,1,30)
x_sample = torch.from_numpy(x)
x_sample = x_sample.unsqueeze(1)
x_sample = torch.cat([x_sample ** i for i in range(1,4)] , 1)
x_sample = x_sample.float()
y_actural = f(x_sample)
tt = x_sample.cuda()
y_predict = model(tt)
plt.plot(x,y_actural.numpy(),'ro',x,y_predict.data.cpu().numpy())
plt.legend(['real point','fit'])
plt.show()