二分查找万能模板

相信大家在各处都看到了很多关于二分查找的模板，我在阅读了众多二分查找的模板后，发现了一个最好理解也是最好用的模板，原创来自于b站的五点七边，如果想要进一步了解的话可以去b站看视频，我这里就简单阐述一下思路以及举几道例题分析。

模板思路：我们可以将需要进行二分查找的数组看成一片领域，然后左右两个指针看做成两头老虎，他们要根据所给的条件不断分割这片领域，直到最后这个领域正好被分成两头老虎各自的领域。最后退出循环的时候，左老虎在自己领域的最右边，右老虎在自己领域的最左边，且它们俩彼此相邻。

        

模板写法：

//左边界值为设置为-1，右边界设置为数组的大小
int left = -1, right = nums.size();

//循环条件
while ( left + 1 != right )
{
      //二分查找的mid值
      int mid = ( left + right ) / 2;
      //更新领域,使数组最后变成左右两个领域
      if ( 左领域 )
      {
           //更新左右指针
           left = mid;
      }
      if ( 右领域 )
      {
           //更新右指针
           right = mid;
      }
}
//看要求的结果在哪个领域即返回哪个值
return left/right;

下面通过例题来讲解下模板的具体用法：

一、给定一个数组nums[8]={1,2,3,5,5,5,8,9}，分别要求如下几个问题。

(1)找到第一个>=5的元素

    根据>=5这个条件来划分领域，可以让左边的老虎划分<5的领域，让右边的老虎划分>=5的领域，如图：

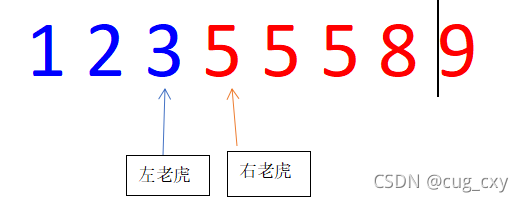
最后他们的领域分别如图所示，且退出循环后，两个指针的指向相邻，下面贴出代码：

//左边界值为设置为-1，右边界设置为数组的大小
int left = 0, right = nums.size();

//循环条件
while ( left + 1 != right )
{
      //二分查找的mid值
      int mid = ( left + right ) / 2;
      //更新领域,使数组最后变成左右两个领域
      if ( nums[mid] < 5 )
      {
           //更新左右指针
           left = mid;
      }
      if ( 右领域 )
      {
           //更新右指针
           right = mid;
      }
}
return right;

 (2)找到最后一个<5的元素

     参考上一小问，我们只需最后返回指针即可。

(3)找到第一个>5的元素

    以<=5为分界条件，左边的老虎获得<=5的领域，右边的老虎获得>5的领域，最后返回右边的指针即可。

//左边界值为设置为-1，右边界设置为数组的大小
int left = 0, right = nums.size();

//循环条件
while ( left + 1 != right )
{
      //二分查找的mid值
      int mid = ( left + right ) / 2;
      //更新领域,使数组最后变成左右两个领域
      if ( nums[mid] <= 5 )
      {
           //更新左右指针
           left = mid;
      }
      if ( 右领域 )
      {
           //更新右指针
           right = mid;
      }
}
return right;

(4)找到最后一个<=5的元素

   与第三问类似，返回左指针即可。

二、给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

    题目中给定数组是升序，我们因此可以联想到使用二分查找法，并且套用我们上面的讲述的模板。

（1)先找到目标值出现的第一个位置，以target为分界点，小于target的为左边领域，另一变自然是大于等于target的领域，具体代码如下

      int left = -1,right = nums.size();
        while ( left + 1 != right )
        {
            int mid = ( left + right ) / 2;
            if( nums[mid] < target )
            {
                left = mid;
            }
            else
            {
                right = mid;
            }
        }
        return right；

(2)找到最后一次出现的位置，我们以小于等于target为左领域，大于target为右领域，最后返回左指针即可

   int left = -1,right = nums.size();
        while ( left + 1 != right )
        {
            int mid = ( left + right ) / 2;
            if( nums[mid] <= target )
            {
                left = mid;
            }
            else
            {
                right = mid;
            }
        }
        return left；

总结: 大家套用此模板时，切记要找好区分左右领域的条件，而且不要弄混了最后需要返回的指针，多多练习方可熟能生巧。

如果觉得对你有帮助，麻烦给作者点个赞，给予支持是我创作的动力。