二叉排序树原理探究(Java实现)

原创 于 2021-05-31 12:54:17 发布 · 200 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #二叉树 #java

二叉排序树(BST)

section1 : 二叉排序树的简介

1.1 什么是二叉排序树

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高

1.2 二叉排序树的定义

一棵空树，或者是具有下列性质的二叉树：

  1. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值
  2. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值
  3. 左、右子树也分别为二叉排序树
  4. 没有键值相等的结点

2. 二叉排序树优势分析

  1. 当使用数组进行数据的操作时: 删除,插入的效率较低,因为涉及到插入,删除点之后数据的移动操作;
  2. 当使用链表进行数据的操作时, 删除,插入数据的效率较高,但是查询的效率很低
  3. 使用BST进行数据的操作, 会按照数据的id值去查找对应的元素,每次递归查询的数据量减半,因此查询效率高于链表; 且能实现像链表类似的增删方式,因此删除和添加效率也可以保证;

3. 二叉排序树实例

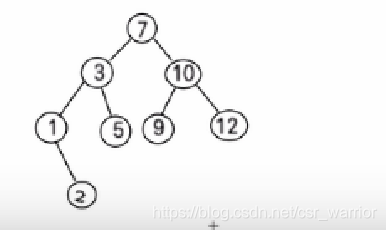
在这里插入图片描述

3.1 创建二叉排序树

3.1.1 创建BST的思路:
  1. 首先定义一个BiarySortTreeNode的类, 作为BST的一个节点对象; 属性包含属性值(int value),指向左子树的指针(BinarySortTreeNode left)和指向右子树的指针(BianrySortTreeNode)right;
  2. 创建一个BiarySortTree的类,把root节点作为类属性
  3. 编写addNode方法, 新增的Node作为参数; 如果判断新节点在BST中所在位置,进行添加操作
  4. 所有节点添加完成后,BST就已经构建完成
3.1.2 代码示例:
public void addNode(BinarySortTreeNode newNode) {
        if (newNode == null) {
            System.out.println("newNode is null!!");
            return;
        }
        if (newNode.getVal() < this.getVal()) {
            //新节点的值小于当前节点的值,挂载到左子树
            if (this.getLeftChild() == null) {
                this.setLeftChild(newNode);
            } else {
                //向左子树递归
                this.leftChild.addNode(newNode);
            }
        } else {
            //新节点的值大于当前节点,挂载到右子树
            if (this.getRightChild() == null) {
                this.setRightChild(newNode);
            } else {
                //向右递归
                this.rightChild.addNode(newNode);
            }
        }
    }

3.2 查找节点

3.2.1 查找节点的思路分析
  1. 若根结点的关键字值等于查找的关键字，成功
  2. 若小于根结点的关键字值，递归查左子树
  3. 若大于根结点的关键字值，递归查右子树
  4. 若子树为空，查找不成功
3.2.2 代码示例:
 public BinarySortTreeNode searchNode(int val) {
        if (this.getVal() == val) {
            return this;
        } else if (val < this.getVal()) {
            if (this.leftChild == null) {
                return null;
            }
            //向左递归查找
            return this.leftChild.searchNode(val);
        } else {
            if (this.rightChild == null) {
                return null;
            }
            //向右递归查找
            return this.rightChild.searchNode(val);
        }
    }

3.3 删除节点

3.3.1 删除节点思路分析

删除节点的情况较复杂,有下面三种情况需要考虑

  1. 删除叶子节点
  2. 删除只有一颗子树的节点
  3. 删除有两颗子树的节点.
1. 删除叶子节点

  1. 先去找到要删除的结点targetNode

  2. 找到targetNode的父结点parentNode;

  3. 确定targetNode是parentNode的左子结点还是右子结点

    • 如果是左子节点: ParentNode.left = null;
    • 如果是右子节点:parentNode.right = null;
2. 删除只有一颗子树的节点
  1. 先去找到要删除的结点targetNode
  2. 找到targetNode的父结点parentNode
  3. 确定targetNode的子结点是左子结点还是右子结点
  4. 如果targetNode有左子结点:

    • 如果targetNode是parentNode的左子节点:

      • parentNode.left = targetNode.left;

    • 如果targetNode是parentNode的右子节点:

      • parentNode.right = targetNode.left;
  5. 如果targetNode有右子节点

    • 如果targetNode是parentNode的左子节点:

      • parentNode.left = targetNode.right;

    • 如果targetNode是parentNode的右子节点:

      • parentNode.right = targetNode.right;
3. 删除有两颗子树的节点
  1. 先去找到要删除的结点targetNode
  2. 找到targetNode的父结点parentNode
  3. 从targetNode的右子树找到最小的结点或者左子树中最小的节点
  4. 用一个临时变量，将最小结点的值保存temp
  5. 删除该最小结点
  6. targetNode.value=temp.value
3.3.2 代码实现
首先先定义两个方法:
  1. 查找父节点的方法
public BinarySortTreeNode searchParentNode(int val) {
        if ((this.leftChild != null && this.leftChild.getVal() == val) || (this.rightChild != null && this.rightChild.getVal() == val)) {
            return this;
        } else if (val < this.getVal() && this.leftChild != null) {
            //左递归
            return this.leftChild.searchParentNode(val);
        } else if (val > this.getVal() && this.rightChild != null) {
            //有递归
            return this.rightChild.searchParentNode(val);
        } else {
            return null;
        }
    }
  1. 查找左子树中最大值的方法
private int deleteMaxNode(BinarySortTreeNode node) {
        BinarySortTreeNode temp = node;
        if (temp == null) {
            return -1;
        }
        while (temp.getRightChild() != null) {
            temp = temp.getRightChild();
        }
        this.deleteNode(temp.getVal());
        return temp.getVal();
    }
删除节点代码实现
//删除节点
    public void deleteNode(int val) {
        if (root == null) {
            return;
        }
        BinarySortTreeNode targetNode = this.searchNode(val);
        //没有找到节点
        if (targetNode == null) {
            return;
        }
        if (root.getLeftChild() == null && root.getRightChild() == null) {
            //只有一个节点
            root = null;
            return;
        }
        //查找targetNode的父节点
        BinarySortTreeNode parentNode = this.root.searchParentNode(val);
        if (targetNode.getLeftChild() == null && targetNode.getRightChild() == null) {
            //左右子树为null,说明是叶子节点
            if (parentNode.getVal() > targetNode.getVal() && parentNode.getLeftChild() != null) {
                //父节点val> 目标节点,说明目标在左侧
                parentNode.setLeftChild(null);
            } else if (parentNode.getVal() <= targetNode.getVal() && parentNode.getRightChild() != null) {
                parentNode.setRightChild(null);
            }
        } else if (targetNode.getLeftChild() != null && targetNode.getRightChild() != null) {
            //左右子树都存在. 从targetNode右子树中寻找最小的节点
            /*int minNode = this.deleteMinNode(targetNode.getRightChild());
            targetNode.setVal(minNode);*/
            int maxNode = this.deleteMaxNode(targetNode.getLeftChild());
            targetNode.setVal(maxNode);
        } else {
            //左右子树存在一个
            if (targetNode.getLeftChild() != null) {
                if (parentNode != null) {
                    //要删除的节点有左子节点
                    if (parentNode.getLeftChild().getVal() == val) {
                        parentNode.setLeftChild(targetNode.getLeftChild());
                    } else {
                        parentNode.setRightChild(targetNode.getLeftChild());
                    }
                } else {
                    root = targetNode.getLeftChild();
                }
            } else {
                //要删除的节点存在右子节点
                if (parentNode != null) {
                    if (parentNode.getRightChild().getVal() == val) {
                        parentNode.setRightChild(targetNode.getRightChild());
                    } else {
                        parentNode.setLeftChild(targetNode.getRightChild());
                    }
                } else {
                    root = targetNode.getRightChild();
                }
            }
        }
    }

4. 完整代码

public class BinarySortTree {
    private BinarySortTreeNode root;

    public BinarySortTree(BinarySortTreeNode root) {
        this.root = root;
    }

    public BinarySortTree() {
    }

    public BinarySortTreeNode getRoot() {
        return root;
    }

    public void setRoot(BinarySortTreeNode root) {
        this.root = root;
    }

    //添加节点
    public void addNode(BinarySortTreeNode node) {
        if (node == null) {
            return;
        }
        this.root.addNode(node);
    }

    public void traverse() {
        if (this.root == null) {
            System.out.println("树为null 无法遍历");
            return;
        }
        this.root.midOrderTraversal();
    }

    public BinarySortTreeNode searchNode(int val) {
        return this.root.searchNode(val);
    }

    public BinarySortTreeNode searchParent(int val) {
        return this.root.searchParentNode(val);
    }

    //删除节点
    public void deleteNode(int val) {
        if (root == null) {
            return;
        }
        BinarySortTreeNode targetNode = this.searchNode(val);
        //没有找到节点
        if (targetNode == null) {
            return;
        }
        if (root.getLeftChild() == null && root.getRightChild() == null) {
            //只有一个节点
            root = null;
            return;
        }
        //查找targetNode的父节点
        BinarySortTreeNode parentNode = this.root.searchParentNode(val);
        if (targetNode.getLeftChild() == null && targetNode.getRightChild() == null) {
            //左右子树为null,说明是叶子节点
            if (parentNode.getVal() > targetNode.getVal() && parentNode.getLeftChild() != null) {
                //父节点val> 目标节点,说明目标在左侧
                parentNode.setLeftChild(null);
            } else if (parentNode.getVal() <= targetNode.getVal() && parentNode.getRightChild() != null) {
                parentNode.setRightChild(null);
            }
        } else if (targetNode.getLeftChild() != null && targetNode.getRightChild() != null) {
            //左右子树都存在. 从targetNode右子树中寻找最小的节点
            /*int minNode = this.deleteMinNode(targetNode.getRightChild());
            targetNode.setVal(minNode);*/
            int maxNode = this.deleteMaxNode(targetNode.getLeftChild());
            targetNode.setVal(maxNode);
        } else {
            //左右子树存在一个
            if (targetNode.getLeftChild() != null) {
                if (parentNode != null) {
                    //要删除的节点有左子节点
                    if (parentNode.getLeftChild().getVal() == val) {
                        parentNode.setLeftChild(targetNode.getLeftChild());
                    } else {
                        parentNode.setRightChild(targetNode.getLeftChild());
                    }
                } else {
                    root = targetNode.getLeftChild();
                }
            } else {
                //要删除的节点存在右子节点
                if (parentNode != null) {
                    if (parentNode.getRightChild().getVal() == val) {
                        parentNode.setRightChild(targetNode.getRightChild());
                    } else {
                        parentNode.setLeftChild(targetNode.getRightChild());
                    }
                } else {
                    root = targetNode.getRightChild();
                }
            }
        }
    }


    //删除并且返回最小节点的值
    private int deleteMinNode(BinarySortTreeNode node) {
        BinarySortTreeNode temp = node;
        if (temp == null) {
            return -1;
        }
        while (temp.getLeftChild() != null) {
            temp = temp.getLeftChild();
        }
        this.deleteNode(temp.getVal());
        return temp.getVal();
    }

    //删除并返回左子树中最大的那个节点的值
    private int deleteMaxNode(BinarySortTreeNode node) {
        BinarySortTreeNode temp = node;
        if (temp == null) {
            return -1;
        }
        while (temp.getRightChild() != null) {
            temp = temp.getRightChild();
        }
        this.deleteNode(temp.getVal());
        return temp.getVal();
    }
}

class BinarySortTreeNode implements TreeTraversal {
    private Integer val; //节点值
    private BinarySortTreeNode leftChild; //左子树
    private BinarySortTreeNode rightChild; //右子树

    public BinarySortTreeNode(Integer val) {
        this.val = val;
        this.leftChild = null;
        this.rightChild = null;
    }

    public Integer getVal() {
        return val;
    }

    public void setVal(Integer val) {
        this.val = val;
    }

    public BinarySortTreeNode getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(BinarySortTreeNode leftChild) {
        this.leftChild = leftChild;
    }

    public BinarySortTreeNode getRightChild() {
        return rightChild;
    }

    public void setRightChild(BinarySortTreeNode rightChild) {
        this.rightChild = rightChild;
    }

    @Override
    public String toString() {
        return "BinarySortTreeNode{" +
                "val=" + val +
                '}';
    }

    public void addNode(BinarySortTreeNode newNode) {
        if (newNode == null) {
            System.out.println("newNode is null!!");
            return;
        }
        if (newNode.getVal() < this.getVal()) {
            //新节点的值小于当前节点的值,挂载到左子树
            if (this.getLeftChild() == null) {
                this.setLeftChild(newNode);
            } else {
                //向左子树递归
                this.leftChild.addNode(newNode);
            }
        } else {
            //新节点的值大于当前节点,挂载到右子树
            if (this.getRightChild() == null) {
                this.setRightChild(newNode);
            } else {
                //向右递归
                this.rightChild.addNode(newNode);
            }
        }
    }

    @Override
    public void preOrderTraversal() {
        System.out.println(this);
        if (this.leftChild != null) {
            this.leftChild.preOrderTraversal();
        }
        if (this.rightChild != null) {
            this.rightChild.preOrderTraversal();
        }
    }

    @Override
    public void midOrderTraversal() {
        if (this.leftChild != null) {
            this.leftChild.midOrderTraversal();
        }

        System.out.println(this);
        if (this.rightChild != null) {
            this.rightChild.midOrderTraversal();
        }
    }

    //查找节点
    public BinarySortTreeNode searchNode(int val) {
        if (this.getVal() == val) {
            return this;
        } else if (val < this.getVal()) {
            if (this.leftChild == null) {
                return null;
            }
            //向左递归查找
            return this.leftChild.searchNode(val);
        } else {
            if (this.rightChild == null) {
                return null;
            }
            //向右递归查找
            return this.rightChild.searchNode(val);
        }
    }

    //查找父节点
    public BinarySortTreeNode searchParentNode(int val) {
        if ((this.leftChild != null && this.leftChild.getVal() == val) || (this.rightChild != null && this.rightChild.getVal() == val)) {
            return this;
        } else if (val < this.getVal() && this.leftChild != null) {
            //左递归
            return this.leftChild.searchParentNode(val);
        } else if (val > this.getVal() && this.rightChild != null) {
            //有递归
            return this.rightChild.searchParentNode(val);
        } else {
            return null;
        }
    }
}

5. 总结

BST中给定值的比较次数等于给定值节点在二叉排序树中的层数。如果二叉排序树是平衡的，则n个节点的二叉排序树的高度为Log 2n+1,其查找效率为O(Log 2n)，近似于折半查找。如果二叉排序树完全不平衡，则其深度可达到n，查找效率为O(n)，退化为顺序查找。一般的，二叉排序树的查找性能在O(Log 2n)到O(n)之间。因此，为了获得较好的查找性能，就要构造一棵平衡的二叉排序树。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值