NEFU OJ 2348 小蓝与斐波拉契数列

Time Limit:1000ms
Memory Limit:65535K

Description

Samples

Input 1

6

Output 1

21

Input 2

99999

Output 2

803980321

Hint

1<=n<=100000

Solution

分析一下题目，题目要求斐波那契的第 F(n) 项，F(F(n)) 的值。
数据范围很大，所以 显然 易知 易证 是有规律的。。。

首先设 $t=F(n)$ 计算 $n$ 对 $F(t)$ 的周期 $T1$
$F(F(n))=F(t\mathrm{m}\mathrm{o}\mathrm{d}T1)\mathrm{m}\mathrm{o}\mathrm{d}MOD$

然后再计算 $t$ 中 $n$ 对 $T1$ 的周期 $T2$
$F(F(n))=F(F(n\mathrm{m}\mathrm{o}\mathrm{d}T2)\mathrm{m}\mathrm{o}\mathrm{d}T1)\mathrm{m}\mathrm{o}\mathrm{d}MOD$

经过周期的计算发现 $T1=2000000016$ 仍然很大，所以可以用矩阵快速幂防止递推超时。
矩阵快速幂计算斐波那契数列原理详见 这篇文章。

Code

Part 1 周期计算

代码部分数组 $a[p]$ 为第 $n$ 项， $a[!p]$ 为第 $n+1$，因此周期为 $n-1$

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main()
{
	ll n=0,a[2]={0,1},p=0,mod=1e9+7,cnt=0,T1;
	while(1)
	{
		a[p]=(a[0]+a[1])%mod;
		p=!p;
		n++;
		if(a[p]==1&&a[!p]==1)cnt++;
		if(cnt==2)break;
	}
	T1=n-1;
	cout<<"T1 = "<<T1<<"\n";
	a[0]=0;a[1]=1;p=0;cnt=0;n=0;
	while(1)
	{
		a[p]=(a[0]+a[1])%T1;
		p=!p;
		n++;
		if(a[p]==1&&a[!p]==1)cnt++;
		if(cnt==2)break;
	}
	cout<<"T2 = "<<n-1;
	return 0;
}

运行结果：

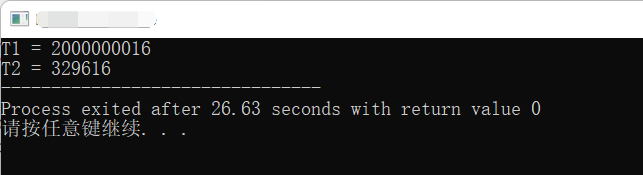
Part 2 题目代码

注意：本题数据范围 $1\le n\le 100000$ 不需要考虑 $n=0$ 的情况。
如果 $n$ 的数据范围包含 0 则需要额外进行判断。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll; 

ll n,k;
ll T1=2000000016;
ll T2=329616;
ll mod=1e9+7;

class Matrix
{
public:
	static Matrix unit;
	ll data[2][2]={{0}};
	int n,m;
	
	Matrix(int nIn,int mIn):n(nIn), m(mIn){}
	
	Matrix mul(Matrix &mat, ll md)
	{
		Matrix tmp=Matrix::unit;
		tmp.n=this->n;
		tmp.m=mat.m;
		for(int i=0;i<this->n;i++)
		{
			for(int j=0;j<mat.m;j++)
			{
				tmp.data[i][j] = 0;
				for(int k=0;k<this->m;k++)
				{
					tmp.data[i][j] += this->data[i][k]*mat.data[k][j]%md;
					tmp.data[i][j] %= md;
				}
			}
		}
		return tmp;
	}
	
	void print()
	{
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				if(j!=0)cout<<" ";
				cout<<this->data[i][j];
			}
			cout<<"\n";
		}
	}
};

Matrix Matrix::unit(2,2);
Matrix mat(2,2);

Matrix qpow(Matrix m1,ll b,ll mod)
{
	Matrix ans=Matrix::unit;
	while(b>0)
	{
		if(b&1)ans=ans.mul(m1,mod);
		m1=m1.mul(m1,mod);
		b>>=1;
	}
	return ans;
}

int main()
{
	cin>>n;
	Matrix::unit.data[0][0]=Matrix::unit.data[1][1]=1;
	mat.data[0][0]=mat.data[0][1]=mat.data[1][0]=1;
	mat=qpow(mat,n%T2-1,T1);
	n=mat.data[0][0];
	mat.data[0][0]=mat.data[0][1]=mat.data[1][0]=1;
	mat.data[1][1]=0;
	mat=qpow(mat,n-1,mod);
	cout<<mat.data[0][0];
	return 0;
}

---

参考文章：https://www.cnblogs.com/dfsac/p/7587784.html