leetcode11 盛最多水的容器-优快云博客

本文链接：https://blog.youkuaiyun.com/csdnnmbdybb/article/details/103109102

本文通过证明展示了一种解决盛水问题的有效算法。关键在于理解两个指针法，一个从首部开始，另一个从尾部开始，两者向中间移动。每次更新最大面积时，较短的线段向较长的线段方向移动一步。通过定义Area[i][j]表示以i,j为左右区间的面积，利用动态规划思想，递归地计算出最大盛水量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这题的官方题解已经给了解法，这里做个简单的证明。

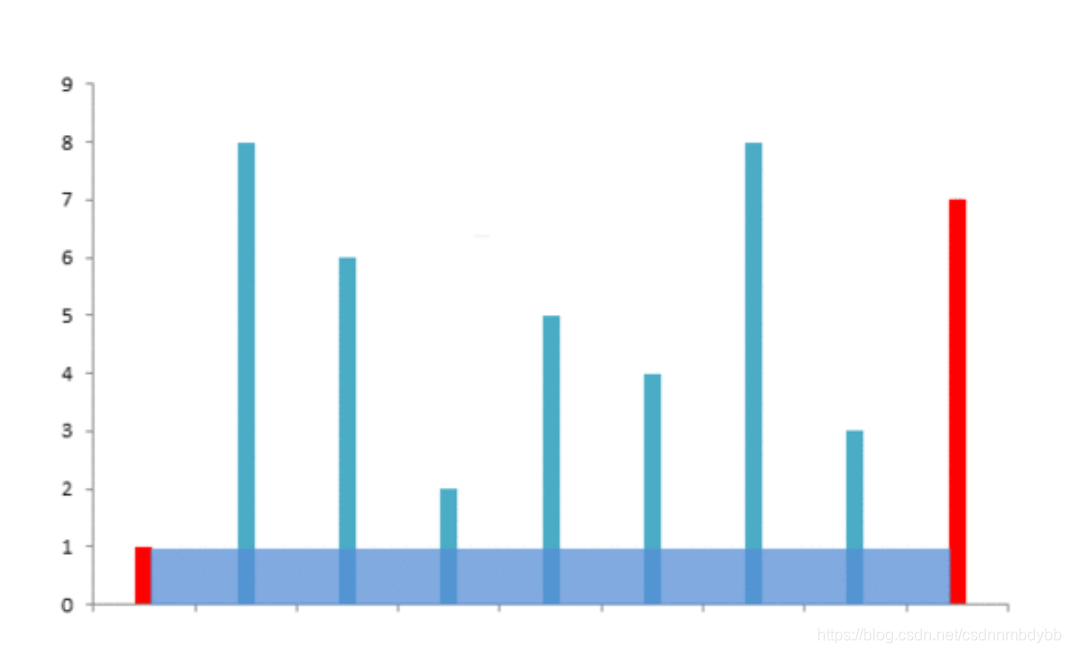
这里盗用下题解中的图；

我们首先概括题解中两个条件：

1. 首尾各一个指针，maxarea存储最大面积

2. 较短的线段往较长的线段方向移动一步。

我们证明时候记录下这个问题的性质：

1. 当我们确定首位指针时候，就意味着我们知道了以该首位为界限的区域的面积,而且这个面积由最短的线段确定高。

2. 为了证明的方便我，我们定义Area[i][j]表示以第i,j为左右区间的面积，根据性质1可知这是很容易计算的。

Area[i][j]=max(H[i]mH[j])*(j-i);

然后用dp[i][j]表示区域i，j中盛水最大的面积，也就是说，dp[0][8]就是我们要求的解。（上图中共有9个竖线）

我们假设H[i]<H[j]; 我们无非有两种走法，首或者尾向对面移动一步。

接下来我们有得到了3个值，Area[i][j],dp[i][j-1],dp[i+1][j];

毫无疑问，我们的dp[i][j]就是上面3个值中的最大值。

3. 我们证明Area[i][j]>Area[i][j-1];根据条件1就能得到。

dp[i][j]=max(Area[i,j],dp[i][j-1],dp[i+1][j])
仿照上面写出下面两个
dp[i+1][j]=max(Area[i+1,j],dp[i+1][j-1],dp[i+2][j])
dp[i][j-1]=max(Area[i,j-1],dp[i+1][j-1],dp[i][j-2])

下面依次比较dp[i][j-1]中各项
因为Area[i,j-1]<Area[i,j];
    dp[i+1][j-1]与dp[i+1][j]中重复；
    dp[i][j-2]其实可以无限递归到dp[i][i+1]（其余项均小于另外两项）,必然小于Area[i,j];
所以，递归的时候
dp[i][j]=max(Area[i,j],dp[i+1,j]);