👂 Rush E (Impossible Version) - Sheet Music Boss - 单曲 - 网易云音乐
👂 My Favorite Things - 羊毛とおはな - 单曲 - 网易云音乐
目录
🌼前言
跟着博客完整看一遍,AC一遍所有题,你就勉强学会高精度了(ง •_•)ง
--> 最近在学《算法训练营入门篇》
--> 需要结合洛谷官方题单
--> 洛谷官方题单,贪心题型里,遇到了一道涉及高精度的题“国王的游戏”
--> 所以花几个小时,系统学一下高精度
步骤
1,理论 + 解析 + 模板
结合 1篇Oi-Wiki + 4个B站视频
2,刷题
New Oj五道题
看了下理论,加很简单,减需要处理下小 - 大,乘需要找规律,除则分2类题型分别找规律
建议看理论时,自己在草稿纸 / 键盘模拟一遍竖式,助于理解
🌼理论
帮大家筛选了一些好的博客和视频(看一遍就懂的那种)
视频
加,减,乘
一个视频带你了解高精度计算!再也不用担心数据溢出了!_哔哩哔哩_bilibili
乘
除1
除2
博客
建议先1.5倍速看完视频,再看博客
高精度计算,也称大整数计算,大整数 加,减,乘,除(乘 / 除 还分高精度与低精度混搭)
高精度的本质:
利用字符串模拟数字,再运用类似数学中,竖式的形式,一位一位地计算
思路
截图来源于B站 麦克老实讲算法
1,存储:字符串转整型,输入数组(下标0和1有所区别)
2,分类:
(1)加减硬算
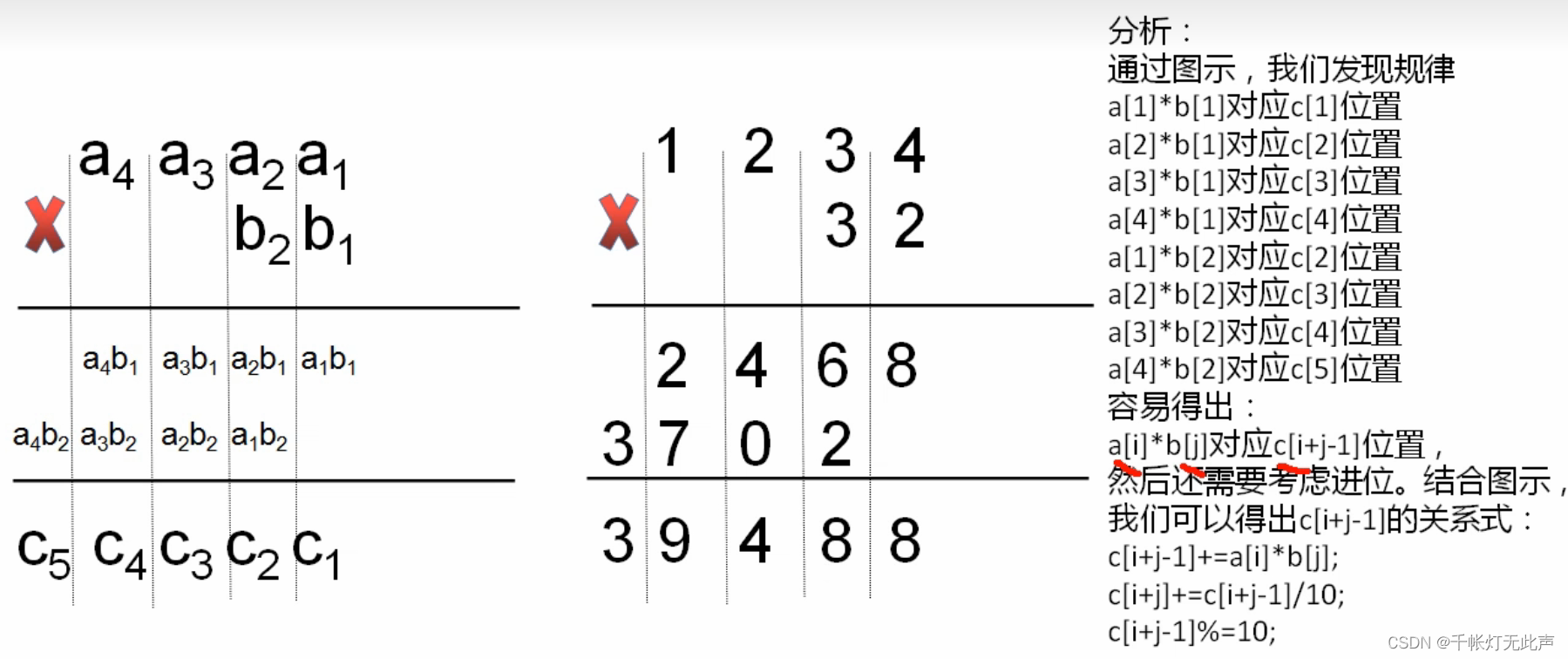
(2)乘法找规律
两层for循环遍历
(3)除法1:高精 / 低精,逐位试商法

(4)除法2:高精 / 高精,减法模拟除法
高精 / 高精是5种高精度里,最难的,建议1.5倍速看2遍视频,结合截图和AC代码中的注释理解,然后自己一定要模拟几次截图,或者跟着视频模拟一遍

3,补充:去除前导0
一层for加个if判断即可去除前导0
低精度可以理解为int, long long, double....可以直接存储
高精度就是长到无法直接用这些类型存储的数字,比如👇
1827391827382739156134576134876519645871654387613745773333333333333333333746573648576384765872687263857624856827349658726583746582736458726348756283476582364587263487562837465872634856238475682376458726348765...🌼理论结合题目
截图来源于B站 麦克老实讲算法
🏆1088: 大整数加法
P1088 - 大整数加法 - New Online Judge (ecustacm.cn)
看注释
AC 代码
#include<iostream>
using namespace std;
int a[1010], b[1010], c[1010];
int main()
{
string s1, s2;
cin>>s1>>s2; //作为字符串输入
int len1 = s1.length(), len2 = s2.length();
//转整型存入数组
for(int i = 0; i < len1; ++i)
a[i] = s1[len1 - i - 1] - '0'; //从小开始存
for(int i = 0; i < len2; ++i)
b[i] = s2[len2 - i - 1] - '0';
//得到较大数的长度
int len = max(len1, len2);
//按位相加
for(int i = 0; i < len; ++i) {
c[i] += a[i] + b[i]; //注意 +=
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
//输出
if(c[len] != 0) len++; //相加后长度增加
for(int i = len - 1; i >= 0; --i)
cout<<c[i];
return 0;
}
3297419374129481729874319287439812312957616548765481364587168576184658164582734
53827459827439875238745987544873875948729347592473592347592374598273945723
3297473201589309169749558033427357186833565278113073838179516168559256438528457🏆1089: 大整数减法
P1089 - 大整数减法 - New Online Judge (ecustacm.cn)
第一次敲,AC 90%,有个很坑的地方,一开始以为是String类字符串的比较出问题了
就是2 > 100,因为它会按顺序比较,2 > 1所以 2 > 100,只需加个len的比较就行
我的问题是,当100 - 100会没有输出,最后补充个相等时,输出的0就行
AC 代码
#include<iostream>
using namespace std;
int a[1010], b[1010], c[1010];
void read(int a[], string s)
{
int len = s.length();
for(int i = 0; i < len; ++i)
a[i] = s[len - i - 1] - '0'; //从低位读入
}
int main()
{
string s1, s2;
int len1, len2;
cin>>s1>>s2; //作为字符串输入
len1 = s1.length(), len2 = s2.length();
if(len1 < len2 || (s1 < s2 && len1 == len2)) {//小的 - 大的
cout<<"-"; //提前输出个负号
len1 = s2.length(), len2 = s1.length();
//读入数组
read(a, s2); //大的读入a[]
read(b, s1); //小的读入b[]
}
else {
//读入数组
read(a, s1); //大的读入a[]
read(b, s2); //小的读入b[]
}
//执行上述操作后, a[]的数更大, len1更大
//按位相减
for(int i = 0; i < len1; ++i) {
c[i] += a[i] - b[i]; //注意+=
if(c[i] < 0) { //借位
c[i + 1] -= 1;
c[i] += 10;
}
}
//排除前导0
int k;
for(k = len1 - 1; k >= 0; --k)
if(c[k] != 0) break;
//输出
for(int i = k; i >= 0; --i)
cout<<c[i];
//补充一个很坑的点
if(len1 == len2 && s1 == s2)
cout<<0;
return 0;
}
几组输出
100
100
0
5858
5959
-101
3535
34341
-30806🏆1090: 大整数乘法
P1090 - 大整数乘法 - New Online Judge (ecustacm.cn)
上面乘法规律的图中,是c[i + j - 1] += a[i] * b[j];
此时下标0开始会越界,出现-1,所以下标从1开始输入数组
,此时c[1 + 1 - 1] += a[1] * b[1],就不受影响
下标从1开始后,相应的s1, s2, a[], b[], c[]的下标也要全部改变
AC 代码
第一次敲完,又是90%,跟减法一样的错误,漏了为0的情况
#include<iostream>
using namespace std;
int a[1010], b[1010], c[2010]; //2010防止溢出
int main()
{
string s1, s2;
cin>>s1>>s2;
int n = s1.length(), m = s2.length(); //字符串长度
//读入数组
for(int i = 1; i <= n; ++i)
a[i] = s1[n - i] - '0'; //最低位读入数组前面
for(int i = 1; i <= m; ++i)
b[i] = s2[m - i] - '0';
//按位相乘
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j) {
c[i + j - 1] += a[i] * b[j];
//每次乘完后进位
c[i + j] += c[i + j - 1] / 10;
c[i + j - 1] %= 10;
}
//排除前导0
int k;
for(k = n + m + 1; k >= 1; --k)
if(c[k] != 0) break;
//逆序, 大到小输出
for(int i = k; i >= 1; --i)
cout<<c[i];
//补充存在一个是0的情况
if((n == 1 && s1[0] == '0') || (m == 1 && s2[0] == '0'))
cout<<0;
return 0;
}
几个测试
123809128390 0
0
19 6
114
381247923749174398123947128347912374918237 932894898437192874398127394871
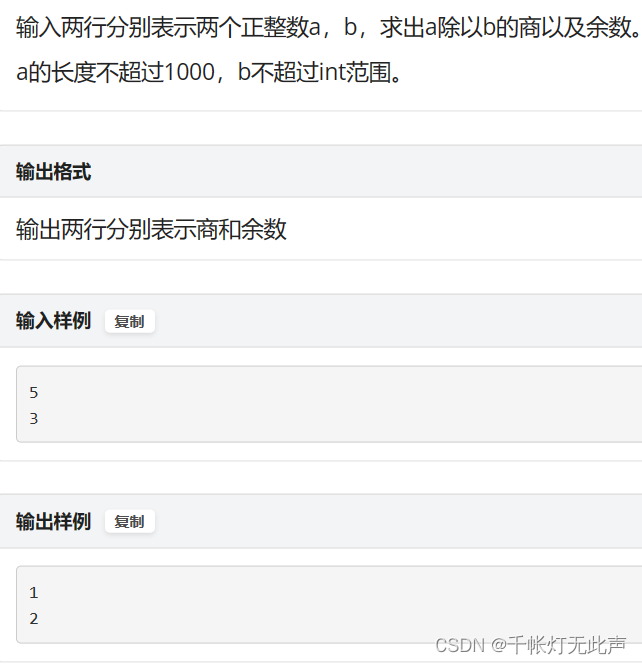
355664243105376703364270700582783731140893607514391377000718338438162427🏆1091: 大整数除法(一)
P1091 - 大整数除法(一) - New Online Judge (ecustacm.cn)
第一类高精度除法:高精 / 低精
注意判断被除数 < 除数的情况
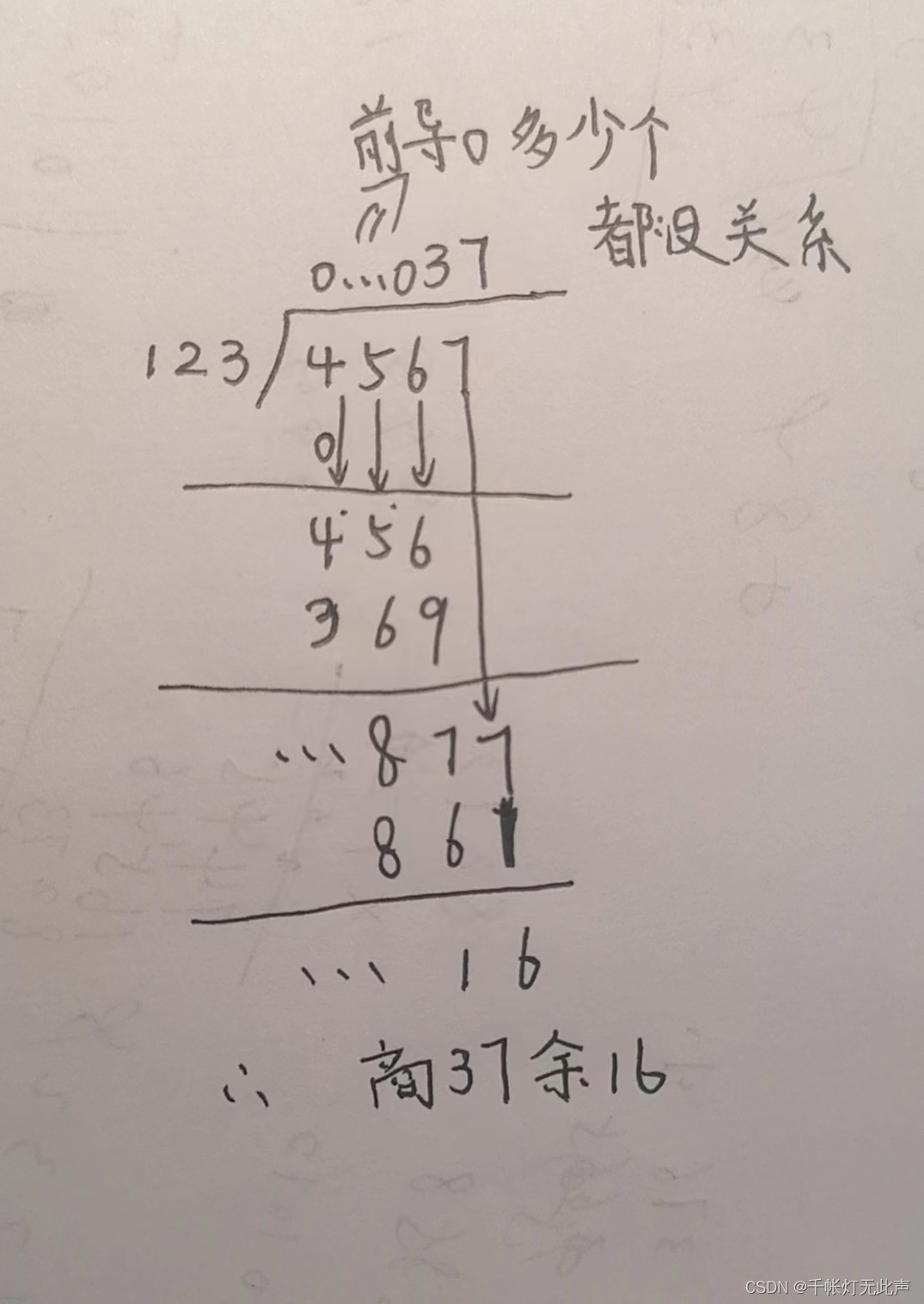
敲代码时,可在草稿纸写出竖式,逐步比对,除数b,余数x,c[]数组的关系
比如4567 / 123👇
第一次AC 40%...还是加了被除 < 除数的判断
于是我去洛谷找了个类似的题
🏆P1480 A/B Problem
P1480 A/B Problem - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
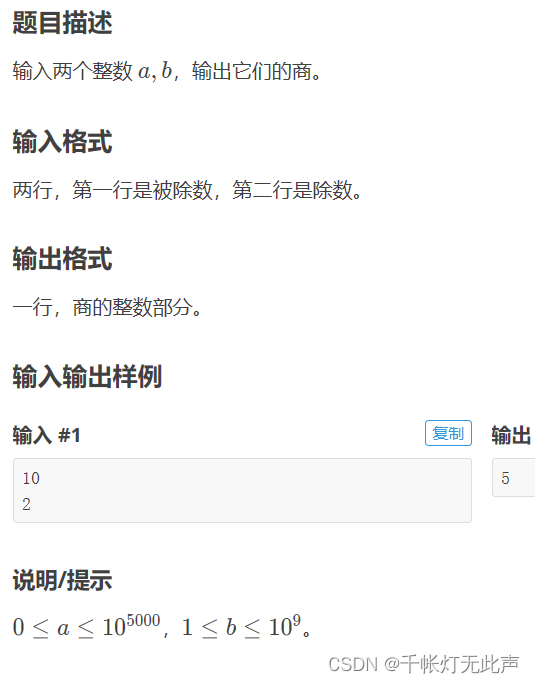
当输入下列数据没有输出9 0
9000000000
1000000000
0
410065408
for(int i = 0; i < n; ++i) { //c[]位数和高精度数组a[]一样
c[i] = (x * 10 + a[i]) / b; //商
x = (x * 10 + a[i]) % b; //余数
}分析
当 i == 0, x = 9 * 10^0, c[0] = 0 ...
当 i == 8, x = 9 * 10^8, c[8] = 0
当 i == 9, x = 9 * 10^9已经越界,改为long long洛谷就能过,然后New Oj也过了(无语。。。
原来只是个long long的BUG,找了半小时)
long long b, x = 0; //b为除数, x为余数洛谷AC 代码
#include<iostream>
using namespace std;
int a[5010], c[5010]; //c[]为答案数组
int main()
{
string s;
//注意开long long!!!
long long b, x = 0; //b为除数, x为余数
cin>>s>>b;
int n = s.length(); //字符串长度
//读入数组
for(int i = 0; i < n; ++i)
a[i] = s[i] - '0'; //最高位读入数组前面
//逐位试商法
for(int i = 0; i < n; ++i) { //c[]位数和高精度数组a[]一样
c[i] = (x * 10 + a[i]) / b; //商
x = (x * 10 + a[i]) % b; //余数
}
//去除前导0
int k;
for(k = 0; k < n; ++k)
if(c[k] != 0) break;
//输出
for(int i = k; i < n; ++i)
cout<<c[i]; //商
//被除数 < 除数的补充
if(k == n && !c[k - 1])
cout<<0; //商为0
//cout<<endl<<x; //余数
return 0;
}
AC 代码
#include<iostream>
using namespace std;
int a[5010], c[5010]; //c[]为答案数组
int main()
{
string s;
//注意开long long!!!否则最后x会越界
long long b, x = 0; //b为除数, x为余数
cin>>s>>b;
int n = s.length(); //字符串长度
//读入数组
for(int i = 0; i < n; ++i)
a[i] = s[i] - '0'; //最高位读入数组前面
//逐位试商法
for(int i = 0; i < n; ++i) { //c[]位数和高精度数组a[]一样
c[i] = (x * 10 + a[i]) / b; //商
x = (x * 10 + a[i]) % b; //余数
}
//去除前导0
int k;
for(k = 0; k < n; ++k)
if(c[k] != 0) break;
//输出
for(int i = k; i < n; ++i)
cout<<c[i]; //商
//被除数 < 除数的补充
if(k == n && !c[k - 1])
cout<<0; //商为0
cout<<endl<<x; //余数
return 0;
}
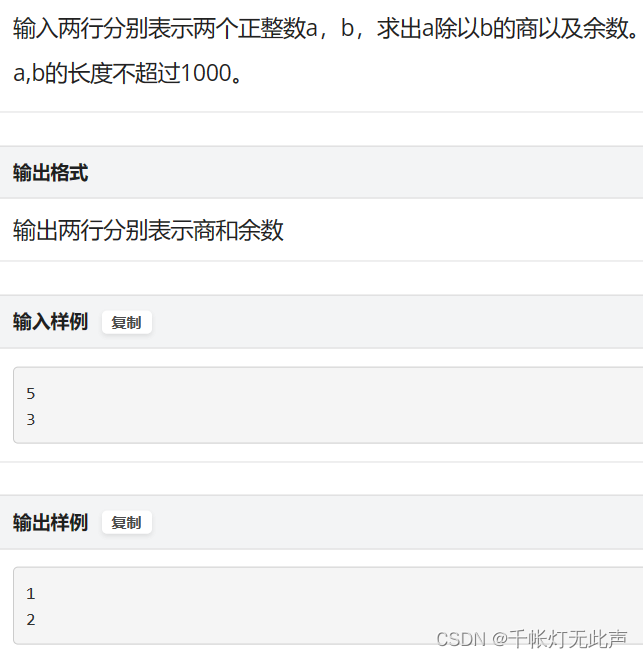
🏆1092: 大整数除法(二)
P1092 - 大整数除法(二) - New Online Judge (ecustacm.cn)
减法模拟除法
需要注意的是,减法,需要高精度减法来实现
同时,由于是高精度减法,需要逆序读入数组,即低位放前面

因为代码较复杂,注意死循环的问题,比如
for(int i = len2 - 1; i >= 0; ++i) {
}犯了习惯性的问题,有时没有输出,不妨看看是不是这个原因
同时,将每个数组的长度保存在a[0], b[0], bb[0], c[0]的位置
那么下标都从1开始
第一次写崩了,思路清晰后重敲了遍
AC 代码
注释占了13行,确实有点长,但思路很清晰
#include<iostream>
#include<cstring> //memset()
using namespace std;
int a[1010], b[1010], c[1010], tmp[1010]; //a被除, b除数, c商
void cpy(int x[], int y[], int n) //x[]左移n位拷贝到y[]
{
for(int i = 1; i <= x[0]; ++i) y[i + n] = x[i];
y[0] = x[0] + n; //y[0]保存该数组大小
}
int compare(int a[], int b[]) //判断是否可以继续减
{
if(a[0] > b[0]) return 1; //a > b, 可以继续减
if(a[0] < b[0]) return -1; //a < b, 不可以继续, 下次循环左移少1位
for(int i = a[0]; i >= 1; --i) { //从高位开始比较
if(a[i] > b[i]) return 1;
if(a[i] < b[i]) return -1;
}
return 0; //相等, 可以再减1次
}
void sub(int a[], int b[]) //高精度减法, 按位相减
{
for(int i = 1; i <= a[0]; ++i) {//低位开始相减, 不足就借位
if(a[i] < b[i]) {
a[i + 1]--; //借位
a[i] += 10;
}
a[i] -= b[i];
}
while(a[a[0]] == 0 && a[0] > 0) a[0]--; //更新a[0], 删除前导0
}
int main()
{
string s1, s2;
cin>>s1>>s2;
//a[0]被除数长度, b[0]除数, c[0]商最大长度
a[0] = s1.size(), b[0] = s2.size(), c[0] = a[0] - b[0] + 1;
//分类讨论: 如果被除数更小
//低位存入数组开头
for(int i = 1; i <= a[0]; ++i) a[i] = s1[a[0] - i] - '0';
for(int i = 1; i <= b[0]; ++i) b[i] = s2[b[0] - i] - '0';
if(a[0] < b[0] || (a[0] == b[0] && s1 < s2))
cout<<0; //商为0
else {
//减法模拟除法
for(int i = c[0]; i >= 1; --i) {
memset(tmp, 0, sizeof(tmp)); //恢复为0
cpy(b, tmp, i - 1); //b[]左移"商 - 1"位, 拷贝到tmp[]
while(compare(a, tmp) >= 0) { //可以继续减
c[i]++; //该位的商 +1
sub(a, tmp); //高精度减法, a[]上按位减去tmp[]
}
}
//去除前导0
int k;
for(k = c[0]; k >= 1; --k)
if(c[k] != 0) break;
//高位开始输出商
for(int i = k; i >= 1; --i)
cout<<c[i]; //商
}
//高位开始输出余数a[]
cout<<endl;
for(int i = a[0]; i >= 1; --i)
cout<<a[i];
return 0;
}
🌼总结
不容易的,编码能力还是挺差,不过比之半年前好了一点点,起码debug的熟练度得到提升
慢慢来,呗,劳逸结合的前提下,尽可能的学习
少点睡到12点才起床
目前每周还是会有4天睡到12点才起,得改改懒惰的性子了
看到这里的朋友,也要上进点~
补充
当然,还有 压位高精度 和 Karatsuba 乘法
想要进阶的可以去Oi-Wiki学学
花了整整一天才写完这个博客,慢慢加油吧





 文章介绍了如何进行高精度计算,包括大整数的加、减、乘、除,并提供了相关的视频教程和博客资源。通过理论学习和刷题实践,详细讲解了每种运算的处理方法,如利用字符串模拟数字,以及处理不同运算中的特殊情况。此外,文章还提到了高精度计算的难点和一些易错点,并给出了一些实际的AC代码示例。
文章介绍了如何进行高精度计算,包括大整数的加、减、乘、除,并提供了相关的视频教程和博客资源。通过理论学习和刷题实践,详细讲解了每种运算的处理方法,如利用字符串模拟数字,以及处理不同运算中的特殊情况。此外,文章还提到了高精度计算的难点和一些易错点,并给出了一些实际的AC代码示例。

















 325
325












