大家好,计算自然语言处理(NLP)是一个迅速发展的领域,其中计算力量与语言学相结合。语言学的一部分主要归功于约翰·鲁珀特·弗斯的分布语义理论,他曾说过以下的名言:“你可以通过其周围的上下文单词来了解一个目标单词”,这表明一个词的语义表示取决于它所在的上下文。
正是基于这一假设,Ashish Vaswani等人的论文“Attention is all you need” 具有重要的开创性,它将Transformer架构设定为许多迅速增长的工具的核心,如BERT、GPT4、Llama等。本文将介绍Transformer架构中编码器部分中的关键处理方法和技术。
1.标记化、embedding和向量空间
在处理NLP问题时,首先要面对的任务是如何对包含在一个句子中的信息进行编码,以便机器能够处理它。机器只能处理数字,这意味着单词、它们的含义、标点符号等都必须被转换为数值表示,这本质上是embedding问题。
在深入讨论embedding是什么之前,需要介绍一个中间步骤,讨论标记化。单词块或单词片段被定义为基本构建块(所谓的标记),稍后将其表示为数字。需要特别注意的是不能用一个数字来刻画一个单词或单词片段,因此使用数字列表(向量)会体现更强的表示能力。
使用将一组单词表示为向量的最简单方式,如果有一个由3个单词组成的句子‘Today is Sunday’,则句子中的每个单词都将用一个向量表示。最简单的形式考虑这仅是3个单词,是一个3维向量空间。例如,可以根据一种一热编码规则为每个单词分配向量:
-
‘Today’ — (1,0,0)
-
‘is’ — (0,1,0)
-
‘sunday’ — (0,0,1)
这个由3维向量组成的结构虽然可以使用,但存在缺点。首先,它以使每个单词与任何其他单词都正交的方式embedding了这些单词,这意味着不能赋予单词之间的语义关系概念。关联向量之间的内积始终为零。
其次,这个特定的结构还可以用于表示由三个不同单词组成的任何其他句子。对于3维空间只能拥有3个线性独立的向量,线性独立意味着集合中的任何向量都不能通过其他向量的线性组合形成。在one-hot编码的背景下,每个向量已经是线性独立的,因此embedding可以处理的单词总数与向量空间的总维数相同。
英语使用者掌握的单词平均数量约为30,000,这意味着需要使用这个大小的向量来处理典型的文本。这样一个高维空间带来了挑战,特别是在内存方面。每个向量只有一个非零分量,这将导致内存和计算资源的非常低效的使用。
为能够描述这个句子的至少一个简单变化,需要扩展向量的大小。在这种情况下,允许使用‘sunday’或‘saturday’,每个单词由一个4维向量空间描述:
‘Today’ — (1,0,0,0)
‘is’ — (0,1,0,0)
‘sunday’ — (0,0,1,0)
‘saturday’ — (0,0,0,1)
3个单词可以堆叠在一起形成一个矩阵X,其中有3行4列:

import numpy as np
from scipy.special import softmax
import math
sentence = "Today is sunday"
vocabulary = ['Today', 'is', 'sunday', 'saturday']
# Initial Embedding (one-hot encoding):
x_1 = [1,0,0,0] # Today
x_2 = [0,1,0,0] # is
x_3 = [0,0,1,0] # Sunday
x_4 = [0,0,0,1] # Saturday
X_example = np.stack([x_1, x_2, x_3], axis=0)
2.单头注意力层:查询、键和值
从X开始,Transformer架构首先通过构建3组其他向量Q、K和V(查询、键和值)来启动。如果在网上查找它们,会发现以下信息:查询是要查找的信息,键是必须提供的信息,而值是实际获得的信息。通过与数据库系统的类比,这确实解释了这些对象的部分信息,但通常认为对其核心理解来自于它们在模型架构中所扮演的角色。
矩阵Q、K和V是通过将X乘以3个其他形状为(4×4)的矩阵W^Q、W^K和W^V而构建的,这些W矩阵包含将在模型训练过程中进行调整的参数,即可学习参数。W最初是随机选择的,并在每个句子(或在实践中是每批句子)的训练过程中进行更新。考虑以下3个W矩阵:
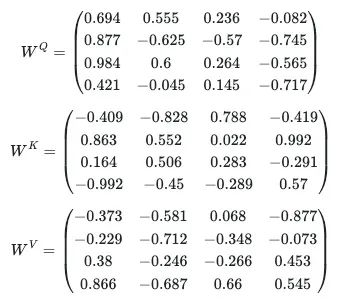
通过从-1到1的均匀分布中进行抽样来创建它们:
W_Q = np.random.uniform(-1, 1, size=(4, 4))
W_K = np.random.uniform(-1, 1, size=(4, 4))
W_V = np.random.uniform(-1, 1, size=(4, 4))
创建一个抽象来存储权重矩阵,以便使用:
class W_matrices:
def __init__(self, n_lines, n_cols):
self.W_Q = np.random.uniform(low=-1, high=1, size=(n_lines, n_cols))
self.W_K = np.random.uniform(low=-1, high=1, size=(n_lines, n_cols))
self.W_V = np.random.uniform(low=-1, high=1, size=(n_lines, n_cols))
def print_W_matrices(self):
print('W_Q : \n', self.W_Q)
print('W_K : \n', self.W_K)
print('W_V : \n', self.W_V)
在与输入X相乘后得到:

Q = np.matmul(X_example, W_Q)
K = np.matmul(X_example, W_K)
V = np.matmul(X_example, W_V)
接下来的步骤是将查询和键矩阵进行点乘,以生成注意力分数,得到的矩阵是Q和K集合中每对向量之间的点积(相似性)的结果:
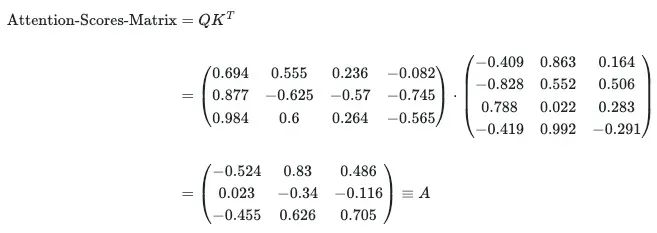
Attention_scores = np.matmul(Q, np.transpose(K))
注意力分数表示空间中向量的接近程度,也就是说对于两个归一化向量,它们的点积越接近1,这些单词彼此更接近,模型考虑了单词在它们出现的句子的上下文中的接近度度量。
矩阵A被除以4的平方根,此操作旨在避免渐变消失/激增的问题。这是因为维度为d_k的两个随机分布的均值为0,标准差为1的向量,产生的标量积也具有均值为0但标准差为d_k。由于下一步涉及对这些标量积值的指数运算,这意味着对于某些值会有很大的因子,如exp(d_k)(考虑到论文中实际使用的维度为512);对于其他值可能会有很小的因子,如exp(−d_k)。
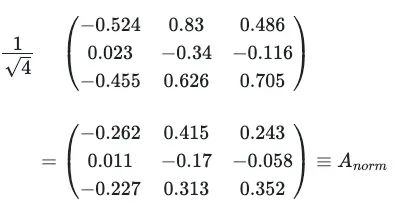
Attention_scores = Attention_scores / 2
应用softmax映射:
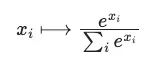
其中x_i是一个通用向量的第i个分量,因此产生了一个概率分布。函数仅对向量定义,而不对二维矩阵定义。当softmax被应用于A_norm时,实际上softmax分别应用于A_norm的每一行(向量)。它假定了一个表示V中每个向量权重的一维向量堆叠的格式,这意味着通常应用于矩阵的操作,比如旋转,在这种情况下是没有意义的。这是因为我们不处理一个连贯的二维实体,而是一组只是碰巧排列在二维格式中的独立向量。
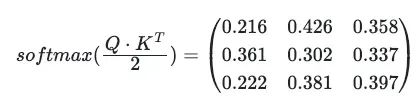
Softmax_Attention_Matrix = np.apply_along_axis(softmax, 1, Attention_scores)
结果乘以V得到单头注意力矩阵,这是初始V(也是初始X)的更新版本:

One_Head_Attention = np.matmul(Softmax_Attention_Matrix, V)
建立一个类来初始化我们的权重矩阵并实现计算单头注意力层的方法,只关心前向传递:
class One_Head_Attention:
def __init__(self, d_model, X):
self.d_model = d_model
self.W_mat = W_matrices(d_model, d_model)
self.Q = np.matmul(X, self.W_mat.W_Q)
self.K = np.matmul(X, self.W_mat.W_K)
self.V = np.matmul(X, self.W_mat.W_V)
def print_QKV(self):
print('Q : \n', self.Q)
print('K : \n', self.K)
print('V : \n', self.V)
def compute_1_head_attention(self):
Attention_scores = np.matmul(self.Q, np.transpose(self.K))
print('Attention_scores before normalization : \n', Attention_scores)
Attention_scores = Attention_scores / np.sqrt(self.d_model)
print('Attention scores after Renormalization: \n ', Attention_scores)
Softmax_Attention_Matrix = np.apply_along_axis(softmax, 1, Attention_scores)
print('result after softmax: \n', Softmax_Attention_Matrix)
# print('Softmax shape: ', Softmax_Attention_Matrix.shape)
result = np.matmul(Softmax_Attention_Matrix, self.V)
print('softmax result multiplied by V: \n', result)
return result
def _backprop(self):
# do smth to update W_mat
pass
3.多头注意力层
将多头注意力定义为在平行中应用此机制ℎ次,每个都有自己的W^Q、W^K和W^V矩阵。在过程结束时有ℎ个自注意力矩阵,称为头部:
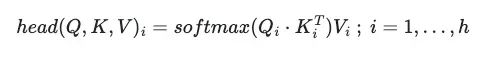
其中Q_i、K_i、V_i由它们各自的权重矩阵W_i^Q、W_i^K和W_i^V相乘定义。在示例中已经计算了一个单头注意力:

考虑第二个头矩阵,经过所有相同计算后,产生以下矩阵:
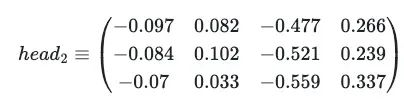
有了单头注意力矩阵,可以将多头注意力定义为所有头部i的串联,再乘以一个新的可学习矩阵W_0:

其中W_0(示例为8×4矩阵)最初是随机初始化的:
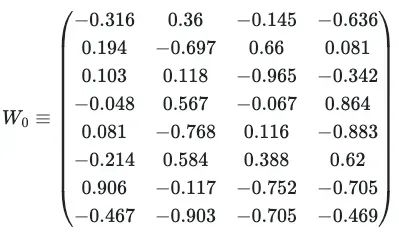
从而得到多头注意力:
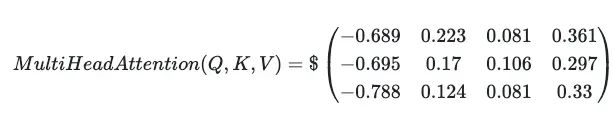
最后将结果添加到初始向量X(一个称为残差连接的操作):

残差连接防止模型陷入渐变消失/激增的问题(再次),其主要思想是当原始X向量添加到矩阵乘法的结果时,每个最终向量的范数被调整为与原始向量的数量级相同。
通过这个过程,将3个4维向量(X的)映射到另一组3个4维向量(更新的V)。现在有3个向量,以某种方式编码句子中出现的单词之间的注意力/语义关系,与最初由简单的one-hot编码算法写下的3个初始向量形成对比。有了这些向量的embedding,以更精细的方式考虑它们在上下文中出现的情况。将多头注意力层实现为一个新类:
class Multi_Head_Attention:
def __init__(self, n_heads, d_model, X):
self.d_model = d_model
self.n_heads = n_heads
self.d_concat = self.d_model*self.n_heads # 4*8
self.W_0 = np.random.uniform(-1, 1, size=(self.d_concat, self.d_model))
# print('W_0 shape : ', self.W_0.shape)
self.heads = []
self.heads_results = []
i = 0
while i < self.n_heads:
self.heads.append(One_Head_Attention(self.d_model, X))
i += 1
def print_W_0(self):
print('W_0 : \n', self.W_0)
def print_QKV_each_head(self):
i = 0
while i < self.n_heads:
print(f'Head {i}: \n')
self.heads[i].print_QKV()
i += 1
def print_W_matrices_each_head(self):
i = 0
while i < self.n_heads:
print(f'Head {i}: \n')
self.heads[i].W_mat.print_W_matrices()
i += 1
def compute(self):
for head in self.heads:
self.heads_results.append(head.compute_1_head_attention())
# print('head: ', self.heads_results[-1].shape)
multi_head_results = np.concatenate(self.heads_results, axis=1)
# print('multi_head_results shape = ', multi_head_results.shape)
V_updated = np.matmul(multi_head_results, self.W_0)
return V_updated
def back_propagate(self):
# backpropagate W_0
# call _backprop for each head
pass
4.位置编码和全连接前向网络
为了简单起见,将向注意机制输入向量的方式没有考虑句子中单词的顺序。显然单词的顺序是它们语义价值的关键元素,因此必须存在于embedding中,通过使用正弦和余弦函数来解决这个问题。它们用于在embedding向量的每个分量中编码顺序,对于出现在句子中的第i个位置的单词,其每个j-th分量与位置编码关联如下:
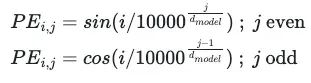
由于PE_i是与embedding向量相同大小的向量,它会添加到它们中以包含单词在句子中所占的位置信息:
![]()
使用这种构建的一个巨大优势在于我们在不需要任何其他空间的情况下包含了新信息。另一个优势是该信息分布在整个向量上,因此通过层中发生的许多矩阵乘法与其他向量的所有其他组件进行通信。现在实现位置编码层:
class Positional_Encoding:
def __init__(self, X):
self.PE_shape = X.shape
self.PE = np.empty(self.PE_shape)
self.d_model = self.PE_shape[1]
def compute(self, X):
for i in range(self.PE_shape[0]):
for j in range(self.PE_shape[1]):
self.PE[i,2*j] = math.sin(i/(10000**(2*j/self.d_model)))
self.PE[i,2*j+1] = math.cos(i/(10000**(2*j/self.d_model)))
# this way we are assuming that the vectors are ordered stacked in X
return X + self.PE
在编码器的末尾,有一个简单的由2层组成的全连接前向网络,通过ReLU激活函数发挥了添加非线性的重要作用,从而捕捉其他语义关联。
class FeedForward(nn.Module):
def __init__(self, d_model, d_ff=2048, dropout=0.1):
super(FeedForward, self).__init__()
self.linear1 = nn.Linear(d_model, d_ff)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(d_ff, d_model)
def forward(self, x):
x = F.relu(self.linear1(x))
x = self.dropout(x)
x = self.linear2(x)
return x
本文从介绍NLP中embedding的概念开始,解释了单词及其语义含义如何被转化为AI模型可以处理的数字形式。进而讲解Transformer架构,从Single-Head Attention层开始,并解释了在该框架中Queries、Keys和Values的作用。接着讨论Attention Scores,对其进行归一化以解决梯度消失和激增的问题。在引导理解单头注意力层的工作方式之后,我们经历了创建多头注意力机制的过程,这使模型能够同时处理和整合输入数据的多个视角。最后介绍位置编码和简单的全连接前向网络,允许保留单词的顺序便于理解句子上下文含义,并通过激活函数起到添加非线性的重要作用。






















 1324
1324

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










