AOE-网（拓扑排序的集成应用）

情景引入：

在生活中，我们会精细规划路线或者安排日程；在工程项目中，我们会细心安排施工流程；在工作中，我们会有先后作业以提高效率......这些场景展示了AOE网在不同领域的应用，它的核心价值在于通过图形化的方式帮助理解和优化复杂系统中的活动顺序和时间管理。

核心解读：

1，AOE-网是一个带权的有向无环图，其中顶点表示事件，弧表示活动，权表示活动持续的时间

2，“路径长度”最长的路径叫关键路径

为了方便求解，我们进行一些假设：

1，活动记为a1,a2,a3......

2,   事件记为v1,v2,v3,v4......

3,活动最早开始时间记为e(i)--a(i)

4,活动最迟开始时间记为L(i)--a(i)

5,满足L(i)=e(i)的活动称为关键活动,想清楚关键路径上的活动全是关键活动！否则会有时间余量

6,事件最早发生时间为Se(j)--v(j)

7,事件最迟发生时间为SL(j)--v(j)

基本思路：求关键路径

(1)输入e条弧{j, k), 建立AOE-网的存储结构；建立AOE网的存储结构，通常使用邻接表来表示

(2)从源点v0出发，令Se[0]=0, 按拓扑有序求其余各顶点的最早发生时间Se[i](1⩽i⩽n-1)。如果得到的拓扑有序序列中顶点个数小于网中顶点数n, 则说明网中存在环，不能求关键路径，算法终止；否则执行步骤

(3)从汇点vn出发，令SL[n-1]=Se[n-1], 按逆拓扑有序求其余各顶点的最迟发生时间SL[i](n-2⩾i⩾2)

(4)根据各顶点的Se和SL值，求每条弧s的最早开始时间e(s)和最迟开始时间L(s)若某条弧满足条件e(s)=L(s), 则为关键活动。

(5),将所有关键活动连接起来，形成关键路径,输出关键路径，这代表了项目的最短完成时间。

代码实现：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>



#define MAX_VERTICES 100
#define INF 999999

int n; // 顶点数
int e; // 边数
int Se[MAX_VERTICES]; // 最早发生时间
int SL[MAX_VERTICES]; // 最迟发生时间
int graph[MAX_VERTICES][MAX_VERTICES]; // 邻接矩阵表示图

// 拓扑排序，计算最早发生时间
int topologicalSort() {
    int indegree[MAX_VERTICES] = { 0 };
    int stack[MAX_VERTICES], top = -1;
    int i, j, k;

    // 计算入度
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            if (graph[i][j] != 0) {
                indegree[j]++;
            }
        }
    }

    // 将所有入度为0的顶点入栈
    for (i = 0; i < n; i++) {
        if (indegree[i] == 0) {
            stack[++top] = i;
        }
    }

    int count = 0;
    while (top != -1) {
        int u = stack[top--];
        Se[u] = (u == 0) ? 0 : Se[u - 1] + graph[u - 1][u]; // 源点的最早发生时间为0
        for (i = 0; i < n; i++) {
            if (graph[u][i] != 0) {
                Se[i] = (Se[i] > Se[u] + graph[u][i]) ? Se[i] : Se[u] + graph[u][i];
                indegree[i]--;
                if (indegree[i] == 0) {
                    stack[++top] = i;
                }
            }
        }
        count++;
    }

    if (count != n) {
        printf("有环\n");
        return 0;
    }
    return 1;
}

// 逆拓扑排序，计算最迟发生时间
void inverseTopologicalSort() {
    int i, j, k;
    for (i = n - 1; i >= 0; i--) {
        for (j = n - 1; j >= 0; j--) {
            if (graph[j][i] != 0) {
                SL[i] = (SL[i] < SL[j] - graph[j][i]) ? SL[i] : SL[j] - graph[j][i];
            }
        }
        SL[i] = (i == n - 1) ? Se[n - 1] : SL[i];
    }
}

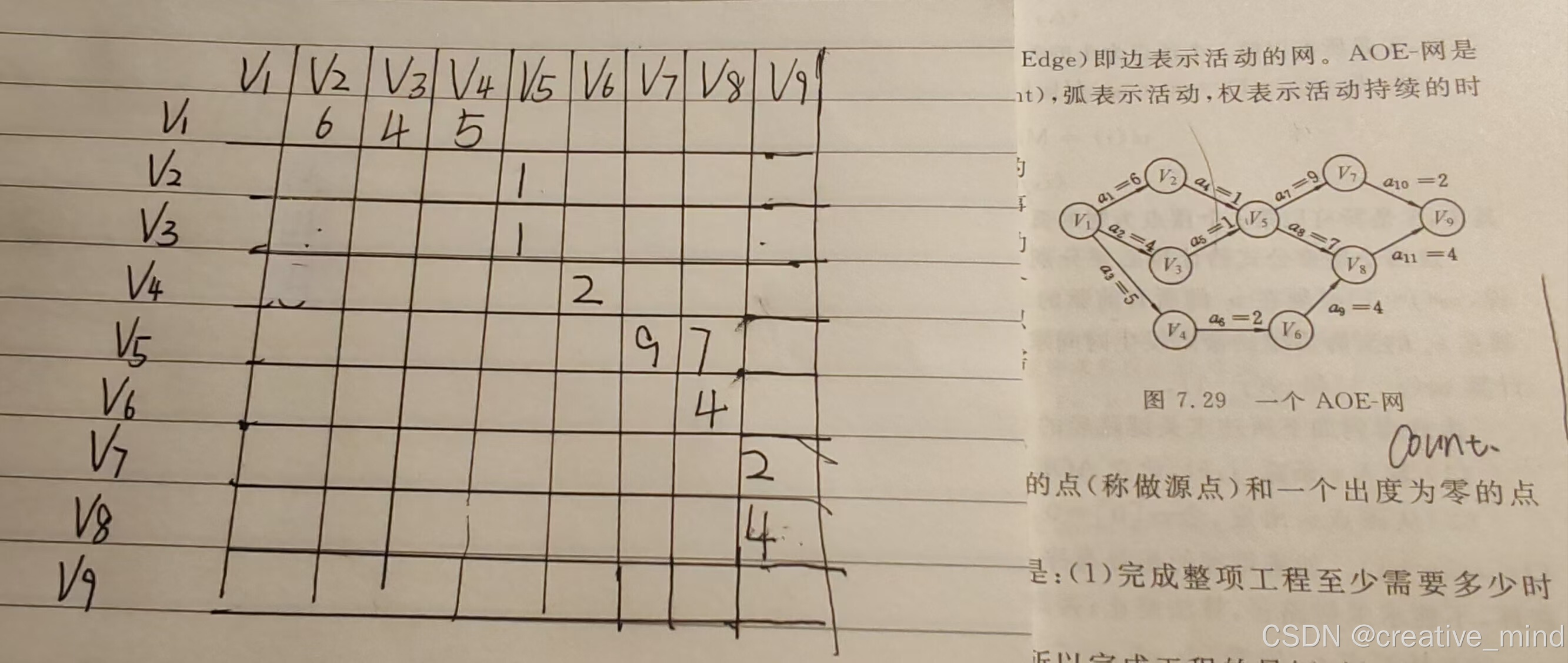
配图理解：

下次再见，最近二个月一直在gitee，望谅解！