滴滴面试：单表可以存200亿数据吗？单表真的只能存2000W，为什么？

尼恩说在前面

在40岁老架构师 尼恩的读者交流群(50+)中，最近有小伙伴拿到了一线互联网企业如得物、阿里、滴滴、极兔、有赞、希音、百度、网易、美团、蚂蚁、得物的面试资格，遇到很多很重要的相关面试题：

问题1：在实际生产环境中，InnoDB 中一棵 B+ 树索引一般有多少层？

问题2：在实际生产环境中，InnoDB一棵B+树可以存放多少行数据？

问题3：MySQL 对于千万级的大表，为啥要优化？

问题4：mysql 单表最好不要超过2000w？

问题5：单表超过2000w 就要考虑数据迁移了，这个是为啥？

问题6：你这个表数据都马上要到2000w 了，难怪查询速度慢，为什么？

问题7：单表能存200亿数据吗？大家都说，单表只存2000W，为什么？

问题8：单表能存200亿数据吗？单表只能存2000W是真的吗，为什么？

问题N： … 第100个变种

最近有小伙伴面试网易，都问到了相关的面试题。 小伙伴没有系统的去梳理和总结，所以支支吾吾的说了几句，面试官不满意，面试挂了。

所以，尼恩给大家做一下系统化、体系化的梳理，使得大家内力猛增，可以充分展示一下大家雄厚的 “技术肌肉”，让面试官爱到 “不能自已、口水直流”，然后实现”offer直提”。

当然，这道面试题，以及参考答案，也会收入咱们的 《尼恩Java面试宝典PDF》V175版本，供后面的小伙伴参考，提升大家的 3高 架构、设计、开发水平。

《尼恩 架构笔记》《尼恩高并发三部曲》《尼恩Java面试宝典》的PDF，请到文末公号【技术自由圈】获取

首先，告诉面试官一个惊世骇俗的答案， 是可以的。

尼恩偷偷的告诉大家， 尼恩在辅导1000多人写简历的过程中， 发现 很多人的单表里边的数据， 都超过了一个亿， 甚至上十个亿。

一点性能问题都没有。

接下来，给面试官做一下 抽丝剥茧的分析， 分析完了， 面试就过了。

接下来，说说 InnoDB 索引数据结构的磁盘文件格式

磁盘扇区、文件系统、InnoDB 存储引擎都有各自的最小存储单元。

来看看三个重要的最小单元

• 磁盘上，存储数据最小单元是扇区，一个扇区的大小是 512 字节，

• 文件系统（例如EXT4）,最小单元是块 （block），一个block 块的大小是 4k，

• InnoDB 存储引擎 的最小储存单元——页（Page），一个页的大小是 16K。

来一个图，更清楚：

由于文件系统（例如EXT4）的最小单元是块 （block），一个block 块的大小是 4k。所以，假设一个文件大小只有1个字节，那么，这个文件在磁盘上，还是不得不占4KB的空间。

具体如下图：

要知道，Innodb 的所有数据文件（后缀为 ibd 的文件），也是存储在磁盘的，当然也是由block组成，

所以，Innodb 的所有数据文件，全部都是 16384（16k）的整数倍。

具体如下图：

InnoDB 存储引擎 的最小储存单元——页（Page），一个页的大小是 16K，

在 MySQL 中我们的InnoDB 页的大小当然也可以通过参数设置的，具体如下图：

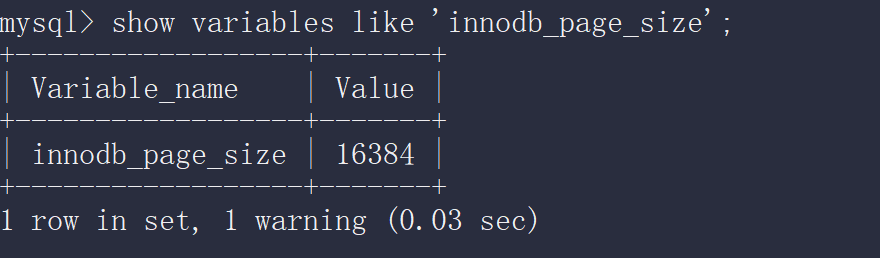
通过上图，可以看到，在 MySQL 中我们的 InnoDB 页的大小默认是 16k

回到核心问题： 一棵B+树可以存放多少行数据？

那么回到我们开始的问题，通常一棵B+树可以存放多少行数据？

高度为2的B+树，可以存放多少行数据?

首先，需要计算出非叶子节点能存放多少指针？

页作为 InnoDB 磁盘管理的最小单位，不仅可以用来存放具体的行数据，还可以存放键值和指针。

回到文题，我们先从简单的入手，

这里我们先假设B+树高为2，即存在一个根节点和若干个叶子节点，那么 B+ 树只有两层。

如下图：

这B+树的存放总记录数为, 是一个简单的公式：

记录总数 = 非叶子节点存放的page 指针数 * 每个叶子节点存放的行记录数

非叶子节点里面存的是主键值 + 指针

为了方便分析，这里我们把一个主键值 + 一个指针称为一个单元，

• 我们假设主键的类型是 BigInt，长度为 8 字节，

• 而指针大小在 InnoDB 中设置为 6 字节，

这样一个单元，一共 14 字节。

这样的话，一页或者说一个非叶子节点能够存放 16384 / 14=1170 个这样的单元。

也就是说一个非叶子节点中能够存放 1170 个指针，即对应 1170 个叶子节点，

叶子节点里面存的是 数据行记录

每个叶子节点存放的行记录数就是每页存放的记录数，由于各个数据表中的字段数量都不一样，这里我们就不深究叶子节点的存储结构了，

实际上现在很多互联网业务数据记录大小通常就是 1K 左右， 简单按照一行记录的数据大小为 1k 来算的话，

一页（16K）或者说一个叶子节点可以存放 16 行这样的数据。

通过简单的公式进行 记录数的估算：

记录总数 = 非叶子节点存放的page 指针数 * 每个叶子节点存放的行记录数

那么 ，这颗2层B+ 树 的非叶子节点（ 唯一的）能够存储多少数据呢？

所以对于这样一棵高度为 2 的 B+ 树，根节点能存放 1170（一个非叶子节点中的指针数） * 16（一个叶子节点中的行数）= 18720 行数据。

尼恩提示，这样分析其实不是很严谨，

为啥呢 ？ InnoDB 数据页结构，不全是 主键值 + 一个指针，还有其他的一些 元数据。按照 《MySQL 技术内幕：InnoDB 存储引擎》中的定义，InnoDB 数据页结构包含如下几个部分：

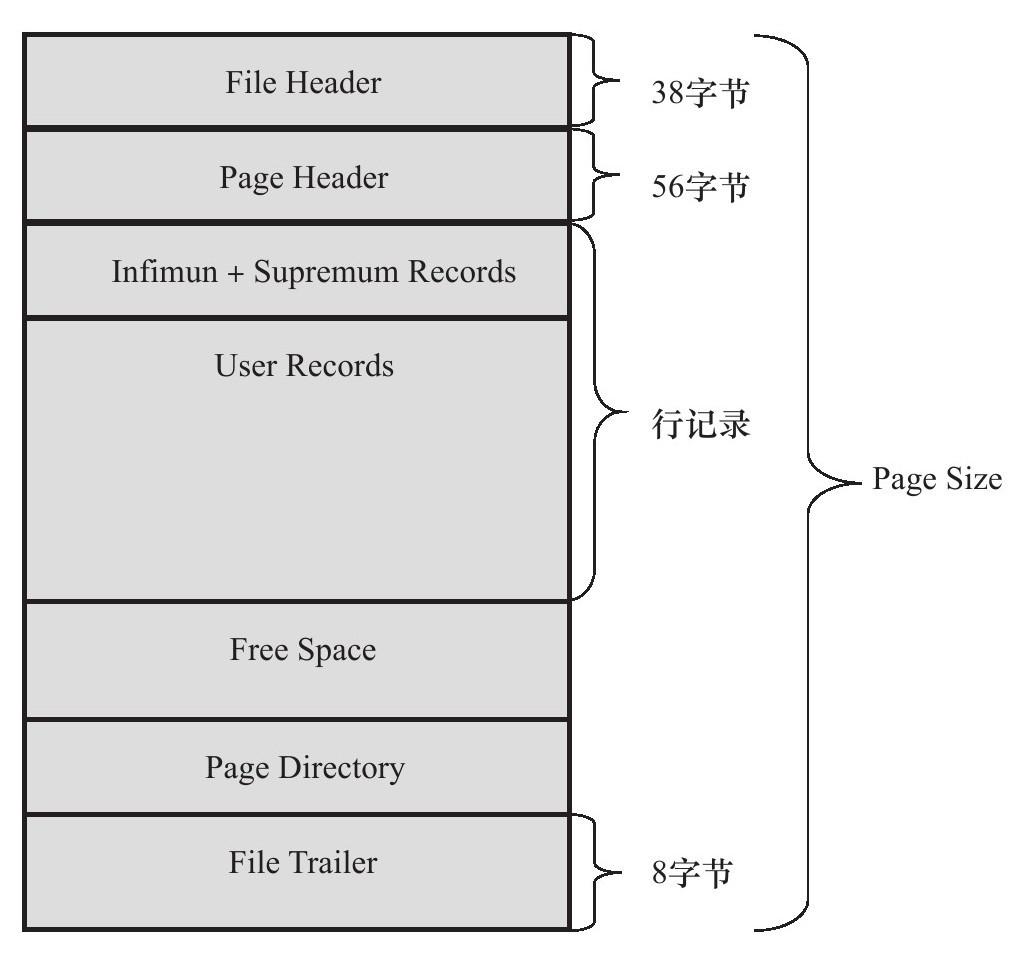
但是咱们这里主要是 估算树的高度和 一颗2层的B+树的大概 容量， 所以就把 他的结构简化理解吧。

高度为3的B+树可以存放多少行数据？

分析完高度为 2 的 B+ 树，同样的道理，我们来看高度为 3 的：

非叶子节点里面存的是主键值 + 指针

为了方便分析，这里我们把一个主键值 + 一个指针称为一个单元，

• 第一层、第二层 都是 非叶节点（索引页）， 用来存储 key + 页指针
• 我们假设主键的类型是 BigInt，长度为 8 字节，
• 而指针大小在 InnoDB 中设置为 6 字节
• 第三层是 叶子， 存储数据 ,是 数据页

这样的话：

• 第一层 根页（page10）可以存放 1170 个指针，有 1170 个二层page

• 第二层的每个页 也都分别可以存放1170个指针，有 1170 * 1170 个 三层 page

叶子节点里面存的是 数据行记录

每条记录 简单按照一行记录的数据大小为 1k 来算的话，一页（16K）或者说一个叶子节点可以存放 16 行这样的数据。

这样， 3层的一共可以存放 1170 * 1170 个指针，即对应的有 1170 * 1170 个叶子节点，每一个叶子节点 可以放大概 16条 record。

所以，高为3的B+树一共可以存放 1170 * 1170 * 16 = 21902400 行记录。

回到问题，InnoDB 一棵 B+ 树可以存放多少行数据？ 这个问题的简单回答是：约 2 千万。

高度为4的B+树可以存放多少行数据？

非叶子节点里面存的是主键值 + 指针

为了方便分析，这里我们把一个主键值 + 一个指针称为一个单元，

• 第一层、第二层、第三层 都是 非叶节点（索引页）， 用来存储 key + 页指针

• 高为3的B+树一共可以存放 1170 * 1170 * * 1170 个 叶子节点 。

叶子节点里面存的是 数据行记录

每条记录 简单按照一行记录的数据大小为 1k 来算的话，一页（16K）或者说一个叶子节点可以存放 16 行这样的数据。

所以，高为4的B+树一共可以存放 1170 * 1170 * 1170 * 16 = 25,625,808,000 （约200亿） 行记录。

回到问题，InnoDB 一棵 B+ 树可以存放多少行数