算法杂项~

原创 已于 2024-09-30 20:09:08 修改 · 376 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #c++ #数据结构

于 2024-04-17 23:09:34 首次发布

1.并查集

具体介绍：

【算法与数据结构】—— 并查集-优快云博客

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 101;

int pre[N], a[N];
int n;

void Init()
{
	for (int i = 0; i < n; i++) pre[i] = i;
	for (int i = 0; i < n; i++) scanf("%d", &a[i]);
}

int Find(int x)
{
	if (x != pre[x]) return pre[x] = Find(pre[x]);
	return pre[x];  
}

void Union(int a, int b)
{
    pre[Find(a)] = Find(b);
}

int main()
{
	cin >> n;
	Init();
}​

这种并查集是最简洁的写法，省去了高度数组，寻找代表的时候使用了高效的递归

2.快速幂

用途：用于快速的求某数的幂

原理分析:

快速幂，龟速乘和快速乘_海龟编辑器a的b次方怎么求-优快云博客

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
LL a, b;

LL f(LL a, LL b)
{
	LL res = 1;

	while (b)
	{
		if (b & 1) res *= a;
		b >>= 1;
		a *= a;
	}
	return res;
}

int main()
{
	cin >> a >> b;
	cout << f(a, b);
}

3.龟速乘

用途：可以慢慢的求值与值的乘积，防止爆变量的最大长度（比如爆int）

原理分析：

快速幂，龟速乘和快速乘_海龟编辑器a的b次方怎么求-优快云博客

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
LL a, b;

LL f(LL a, LL b)
{
	LL res = 0;

	while (b)
	{
		if (b & 1) res += a;
		b >>= 1;
		a += a;
	}
	return res;
}

int main()
{
	cin >> a >> b;
	cout << f(a, b);
}

4.快速幂取模

用途：在快速幂上进行取模操作

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
LL a, b, mod;

LL f(LL a, LL b, int mod)
{
	LL res = 1;

	while (b)
	{
		if (b & 1) res = (res * a) % mod;
		b >>= 1;
		a = (a * a) % mod;
	}
	return res;
}


int main()
{
	cin >> a >> b >> mod;
	cout << f(a, b, mod);
}

5.龟速乘取模

用途：在龟速乘上进行取模操作

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

LL a, b, mod;

LL f(LL a, LL b, int mod)
{
	LL res = 0;

	while (b)
	{
		if (b & 1) res = (res + a) % mod;
		b >>= 1;
		a = (a + a) % mod;
	}
	return res;
}

int main()
{
	cin >> a >> b >> mod;
	cout << f(a, b, mod);
}

6.快速幂取模优化(结合龟速乘取模)

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

LL a, b, mod;

LL f1(LL a, LL b, int mod)
{
	LL res = 0;

	while (b)
	{
		if (b & 1) res = (res + a) % mod;
		b >>= 1;
		a = (a + a) % mod;
	}
	return res;
}

LL f2(LL a, LL b, int mod)
{
	LL res = 1;

	while (b)
	{
		if (b & 1) res = f1(a, b, mod) % mod;
		b >>= 1;
		a = f1(a, a, mod) % mod;
	}
	return res;
}

int main()
{
	cin >> a >> b >> mod;
	cout << f2(a, b, mod);
}

7.矩阵快速幂

就是把快速幂中的数字换成了矩阵

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

#define MAX 100

struct Martix 
{
	int row;	// 行 
	int col;	// 列 
	int martix[MAX][MAX];

	Martix(int r, int c) : row(r), col(c) {} // 构造函数 
};

Martix Multiply(Martix x, Martix y)//求两个矩阵的乘积
{
	Martix z(x.row, y.col);

	for (int i = 0; i < z.row; i++) 
	{
		for (int j = 0; j < z.col; j++) 
		{
			z.martix[i][j] = 0;
			for (int k = 0; k < x.col; k++)
				z.martix[i][j] += x.martix[i][k] * y.martix[k][j];
		}
	}

	return z;
}

Martix Power(Martix x, int k)
{
	Martix r(x.row, x.col);

	// 单位矩阵构建 
	for (int i = 0; i < r.row; i++) 
	{
		for (int j = 0; j < r.col; j++) 
		{
			if (i == j) r.martix[i][j] = 1;
			else r.martix[i][j] = 0;
		}
	}

	// 矩阵快速幂 
	while (k != 0) 
	{
		if (k & 1)
			r = Multiply(x, r);
		k = k >> 1;
		x = Multiply(x, x);
	}

	return r;
}

int main()
{
	int r, k;

	printf("请输入行（列）：\n");
	scanf("%d", &r);
	Martix x(r, r);

	printf("请输入%d行%d列的矩阵：\n", r, r);
	for (int i = 0; i < x.row; i++)
		for (int j = 0; j < x.col; j++)
			scanf("%d", &x.martix[i][j]);

	printf("请输入指数k：\n");
	scanf("%d", &k);

	Martix result = Power(x, k);

	printf("结果是：\n");
	for (int i = 0; i < result.row; i++) 
	{
		for (int j = 0; j < result.col; j++)
			printf("%d ", result.martix[i][j]);
		printf("\n");
	}
}​

8.一维前缀和

用途：方便对一位数组进行区间处理

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;

int s[N], n, temp;//s[N]是前缀和数组

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &temp);
		s[i] = s[i - 1] + temp;//求一维前缀和
	}

	for (int i = 1; i <= n; i++) printf("%d ", s[i] - s[i - 1]);//可以原来求原数组每一项
}

9.二维前缀和

用途：同一维数组

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e3 + 10;

int s[N][N], n, m ,temp;//s[N]是前缀和数组

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &temp);
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + temp;//求二维前缀和
		}
	}

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			printf("%d ", s[i][j] - s[i - 1][j] - s[i][j - 1] + s[i - 1][j - 1]);//也可以取原二维数组的每一项
		}
		cout << endl;
	}
}

10.树状数组

用途：同前缀和，但是搜索时更快

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e3 + 10;

int tree[N], n, temp;


int Lowbit(int x)//求出下标位x的项维护了多长的序列，比如下标为12=0b1100,二进制中存在2个0，那么它维护的序列长度就是2的2次方，即4这么长
//也即求出下标为x的元素在树的第几层且距离其父/子节点的距离是多少
//比如x=12(0b1100)，那么return 4(12的二进制后面有两个0，即处在树的第二层，所以返回二进制的100即返回4)
{
	return x & -x;
}

void Add(int x, int y)
//对树状数组进行修改操作，主要是修改下标为x的元素和其父节点(还有父父……节点)的元素
{
	for (int i = x; i <= n; i += Lowbit(i)) tree[i] += y;
}

int Sum(int x)
//求前缀和
{
	int res = 0;
	for (int i = x; i > 0; i -= Lowbit(i)) res += tree[i];
	return res;
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &temp);
		Add(i, temp);//初始化树状树状
	}

	for (int i = 1; i <= n; i++) printf("%d ", Sum(i) - Sum(i - 1));//可以求出来每一项的值
}

11.线段树

用途：同前缀和，但是搜索时更快

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

#define INF 1e8
const int N = 1e3 + 10;

struct Tree
{
	int l, r;
	int sum = 0;
}tr[N];

int arr[N], n, temp;

void Push_up(int u)//用于通过树的叶节点为上层的节点赋值和更新值
{
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void Build(int u, int l, int r)//创建线段树，u是当前节点下标，l,r是当前节点的左右端点
{
	if (l == r) tr[u] = { l,r,arr[l] };//如果l==r，说明已经递归到叶节点，可以开始赋值
	else
	{
		tr[u] = { l,r };//不是叶节点的节点，先赋值l,r,而sum需要通过Push_up()来完成
		int mid = l + r >> 1;
		Build(u << 1, l, mid);
		Build(u << 1 | 1, mid + 1, r);
		Push_up(u);//给非叶节点赋值sum
	}
}

int GetSum(int u, int l, int r)//获得某一段的数组和，u是当前节点下标，l,r是所需要的一段的左右端点
{
	if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;//如果此时需要的这一段的左右端点已经包含当前这一段，那么返回这一段的sum
	else//否则不断查找，直到把所有的所需要的这一段的值全部获得
	{
		int sum = 0;
		int mid = tr[u].l + tr[u].r >> 1;
		if (l <= mid) sum += GetSum(u << 1, l, r);
		if (r > mid) sum += GetSum(u << 1 | 1, l, r);
		return sum;
	}
}

void Add(int u, int x, int y)//更新元素，u是当前节点下标，x是目标节点，y是需要加上的值
{
	if (tr[u].l == tr[u].r) tr[u].sum += y;//先对叶节点进行更新，然后才能更新该叶节点的各级父节点
	else
	{
		int mid = tr[u].l + tr[u].r >> 1;//查找下标为x的叶节点
		if (x <= mid) Add(u << 1, x, y);
		else if (x > mid)Add(u << 1 | 1, x, y);
		Push_up(u);//逐级更新父节点
	}
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) scanf("%d", &arr[i]);

	Build(1, 1, n);

	for (int i = 1; i <= n; i++) printf("%d ", GetSum(1,i,i));//输出原数组的每一项
}

12.滑动窗口

应用题目：

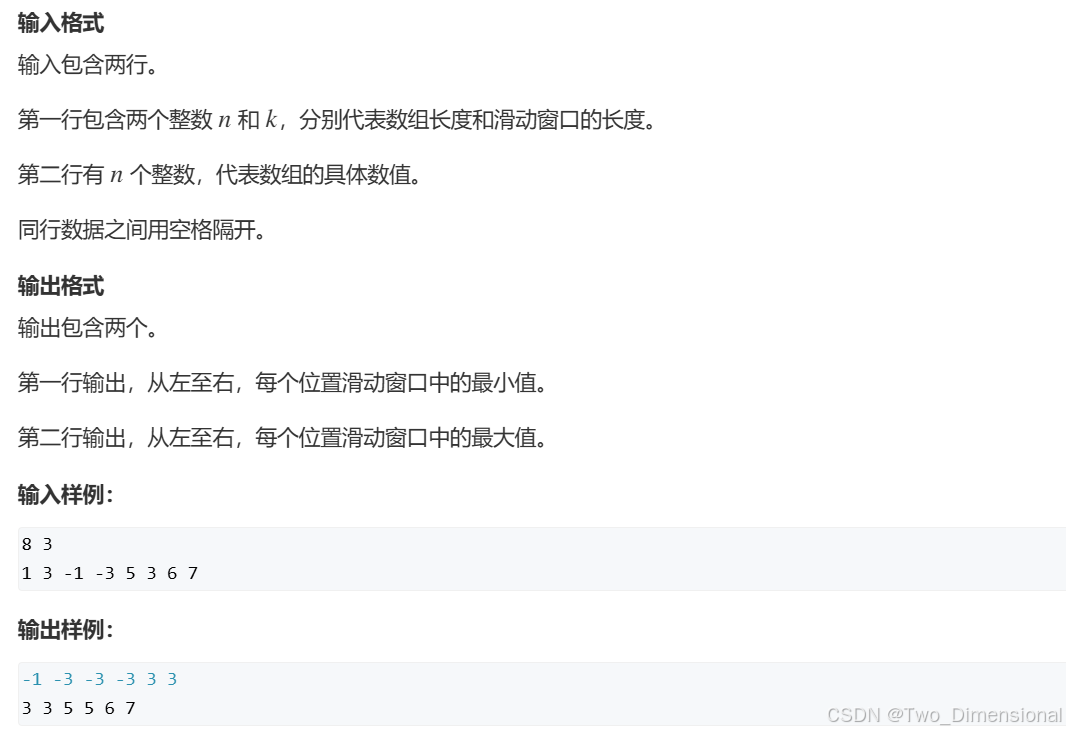
#include<iostream>
#include<vector>
#include<stdio.h>
using namespace std;

const int N = 1000010;
int arr[N],d[N],q[N];
vector<int> v1,v2;

int main(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++) scanf("%d",&arr[i]);

    int h=1,t=0,l=1,r=0;//为两个队列定义头和尾指针
    for(int i=1;i<=n;i++)
    {
        while(t>=h&&arr[d[t]]>=arr[i]) t--;//一旦队列尾元素大于此时遍历到的元素，那么尾指针一直往队列前移动
        while(r>=l&&arr[q[r]]<=arr[i]) r--;//与上一条相反
        d[++t]=i;//队列尾部添加元素
        q[++r]=i;
        if(d[h]<i-k+1) h++;//队列头部已经落后于窗口，那么头指针也向后移动
        if(q[l]<i-k+1) l++;
        if(i>=k) v1.push_back(arr[d[h]]);//当遍历到的下标开始等于窗口大小，开始输出队列头部值
        if(i>=k) v2.push_back(arr[q[l]]);
    }

    for(auto it:v1) printf("%d ",it);
    puts("");
    for(auto it:v2) printf("%d ",it);
}

思路参考：E11【模板】单调队列 滑动窗口最值——信息学竞赛算法_哔哩哔哩_bilibili

13.字符串哈希

重点是前缀和，区间和。

同时注意，h[i]的意思是从左到右数第i个数

参考：F02 字符串哈希_哔哩哔哩_bilibili

14.一些位运算的技巧

1.判断一个数是不是2的幂
#include<iostream>
using namespace std;
// 定义一个函数 f，用于检查 n 是否为正数且为 2 的幂
bool f(int n) 
{
    return n > 0 && n == (n & -n); // 检查 n 是否大于 0 且与其负数的按位与结果相等
}

int main() 
{
    int n; 
    cin >> n; 
    cout << f(n); // 输出 f(n) 的返回值，1 表示 true，0 表示 false
}

2.判断一个数是不是3的幂
#include<iostream>
using namespace std;

bool f(int n)
{
    return n > 0 && 1162261467 % 3 == 0; //1162261467是3在int里面最大的幂值
}

int main()
{
    int n;
    cin >> n;
    cout << f(n);
}

3.>=n的2的最小次幂
#include <iostream>
using namespace std;

int near2power(int n) {
    // 如果 n 小于等于 0，返回 1
    if (n <= 0) {
        return 1;
    }
    
    n--; // 先将 n 减 1
    
    // 执行与运算和右移操作，扩展为下一个最近的 2 的幂次方
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    
    // 返回 n 加 1
    return n + 1;
}

int main() {
    int number = -500;
    cout << near2power(number) << endl;
}

4.获得[left, right]之间所有数&之后的值
#include<iostream>
using namespace std;

int f(int left, int right)
{
    // 当 left 小于 right 时，进入循环
    while(left < right)
        // 减去 right 的最低有效位，right & -right 提取最低有效位的值
        right -= (right & -right);
    // 返回修改后的 right 值
    return right;
}

int main()
{
    int left, right;
    // 输入 left 和 right 的值
    cin >> left >> right;
    // 输出 f 函数的返回值
    cout << f(left, right);
}

5.逆序二进制
#include <iostream>  
  

 // 逆序整数的二进制位  
unsigned int reverseBits(unsigned int n) {  
    n = ((n & 0xAAAAAAAA) >> 1) | ((n & 0x55555555) << 1);  
    n = ((n & 0xCCCCCCCC) >> 2) | ((n & 0x33333333) << 2);  
    n = ((n & 0xF0F0F0F0) >> 4) | ((n & 0x0F0F0F0F) << 4);  
    n = ((n & 0xFF00FF00) >> 8) | ((n & 0x00FF00FF) << 8);  
    n = (n >> 16) | (n << 16);  
    return n;  
}  

  
int main() {  
    unsigned int num = 43261596; // 示例数字  
    cout << ReverseBits::reverseBits(num);   
}

6.二进制中有几个1
#include <stdio.h>  
  
// 计算整数n中1的数量  
int cntOnes(int n) {  
    n = (n & 0x55555555) + ((n >> 1) & 0x55555555);  
    n = (n & 0x33333333) + ((n >> 2) & 0x33333333);  
    n = (n & 0x0f0f0f0f) + ((n >> 4) & 0x0f0f0f0f);  
    n = (n & 0x00ff00ff) + ((n >> 8) & 0x00ff00ff);  
    n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff);  
    return n;  
}  
  
int main() {  
    int num = 0b10101010; // 示例：二进制表示为10101010的整数  
    int result = cntOnes(num);  
    printf("Number of 1s in %d: %d\n", num, result);  
    return 0;  
}

以上6个技巧的来源：算法讲解031【必备】位运算的骚操作_哔哩哔哩_bilibili

15.尺取法（双指针法）（感觉像是滑动窗口变体）

#include<iostream> 
#include<algorithm> 
using namespace std;  

int n, S, a[100010];

void f()  // 定义函数f
{
    int res = n + 1;  // 结果初始化为n+1，表示一个不可能的较大值
    int s = 0, t = 0, sum = 0;  // s和t分别为窗口的起点和终点，sum为窗口中元素的和

    while(1)  // 无限循环
    {
        // 内部循环：窗口的右端t向右扩展，直到sum大于等于S或到达数组末尾
        while(t < n && sum < S) 
            sum += a[t ++];  // 把a[t]加到sum里，t自增
        if(sum < S) break;  // 如果sum仍小于S，跳出外部循环，因为已经无法再构成有效窗口

        res = min(res, t - s);  // 更新最小的子数组长度
        sum -= a[s ++];  // 窗口左端s向右移动，缩小窗口
    }

    if(res > n) cout << 0;  // 如果没有找到符合条件的子数组，输出0
    else cout << res;  // 否则输出找到的最小长度
}

int main()  
{
    cin >> n >> S;  
    for(int i = 0; i < n; i ++) cin >> a[i];  

    f();  
}

16.位图

#include<iostream> 
#include<algorithm>
using namespace std;  

class Bitset 
{
    public:
    int *Arr;  // 定义一个指向整型的指针，用于存储位数组

    void SetNum(int n)  // 设置用于存储的位数组大小
    {
        Arr = new int[(n + 31) / 32];  // 根据输入的n动态分配足够的空间，每32位存储一个整数
        //注意这句做的是向上取整，即需要存储8个数的状态，也需要1个int来实现
    }

    void Add(int x)  // 向位数组中添加元素x
    {
        Arr[x / 32] |= (1 << (x % 32));  // 使用位运算将x对应位置的位设置为1
    }

    void Remove(int x)  // 从位数组中移除元素x
    {
        Arr[x / 32] &= ~(1 << (x % 32));  // 使用位运算将x对应位置的位设置为0
    }

    void Reverse(int x)  // 翻转元素x对应的位
    {
        Arr[x / 32] ^= (1 << Arr[x % 32]);  // 使用位运算翻转x对应位置的位
    }

    bool Contain(int x)  // 判断位数组中是否包含元素x
    {
        return ((Arr[x / 32] >> (x % 32)) & 1) == 1;  // 使用位运算判断x对应的位置是否为1
    }
};



int main() 
{
    Bitset b; 
    int n; 
    cin >> n;  

    b.SetNum(n);  // 调用SetNum函数，设置存储大小
    b.Add(5);  // 将元素5加入到Bitset中
    if(b.Contain(5)) cout << 1 << endl;  // 如果Bitset中包含5，输出1

    b.Remove(5);  // 从Bitset中移除元素5
    if(!b.Contain(5)) cout << 0;  // 如果Bitset中不包含5，输出0
}

思路参考：算法讲解032【必备】位图_哔哩哔哩_bilibili

17.前缀树（class封装写法和单独的全局变量写法）

1.class封装写法（使用链表组成的树）

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;

class Trie
{
    private:
    Trie* root; // 根节点指针

    public:
    int end = 0; // 标记以该节点为结尾的单词个数
    int pass = 0; // 经过该节点的单词个数
    Trie *tries[26]; // 存储26个字母的子节点指针

    Trie()//初始化一个节点
    {
        for(int i =0; i < 26; i ++)
        {
            this->tries[i] = NULL; // 初始化26个子节点为NULL
        }
    }

    void InitRoot()//初始化树中的root
    {
        root = new Trie(); // 初始化根节点
    }

    void Insert(string str)//插入字符串
    {
        Trie* temp = root; // 从根节点开始
        temp->pass ++; // 经过根节点的单词数量+1
        int i;

        for(auto it : str)
        {
            i = it - 'a'; // 计算当前字符在tries数组中的索引
            if(temp->tries[i] == nullptr)
            {
                temp->tries[i] = new Trie(); // 如果对应的子节点不存在，创建一个新节点
            }
            temp->tries[i]->pass ++; // 经过该节点的单词数量+1
            temp = temp->tries[i]; // 将temp移动到当前字符的子节点
        }
        temp->end ++; // 该单词结束的位置标记end+1
    }

    int CountString(string str)//计数有多少个str字符串
    {
        Trie* temp = root; // 从根节点开始
        int i;

        for(auto it : str)
        {
            i = it - 'a'; // 计算当前字符的索引
            if(temp->tries[i] == NULL) return 0; // 如果某个字符的子节点不存在，返回0，表示不存在这个单词
            temp = temp->tries[i]; // 移动到对应的子节点
        }
        return temp->end; // 返回以该节点为结尾的单词数量
    }

    void Remove(string str)//移除一个str
    {
        if(!CountString(str)) return; // 如果该单词不存在，则直接返回

        Trie* temp = root; // 从根节点开始
        int i;
        temp->pass --; // 经过根节点的单词数量-1

        for(auto it : str)
        {
            i = it - 'a'; // 计算当前字符的索引
            if(!(-- temp->tries[i]->pass))  // 如果经过该子节点的单词数量为0
            {
                temp->tries[i] = NULL; // 将该子节点设置为NULL，表示删除
                return; // 删除后直接返回
            }
            temp = temp->tries[i]; // 移动到下一个字符的子节点
        }
        temp->end --; // 该单词结束的节点end-1，表示删除了一个单词
    }

    int CountStringStartWith(string str)//计数有多少个以str为前缀的字符串
    {
        Trie* temp = root; // 从根节点开始
        int i;

        for(auto it : str)
        {
            i = it - 'a'; // 计算当前字符的索引
            if(temp->tries[i] == NULL) return 0; // 如果某个字符的子节点不存在，返回0，表示没有以这个前缀开头的单词
            temp = temp->tries[i]; // 移动到下一个字符的子节点
        }
        return temp->pass; // 返回经过该前缀的单词数量
    }
};

int main()
{
    Trie* root = new Trie(); // 创建Trie的根节点

    root->InitRoot(); // 初始化根节点
    root->Insert("abcdg"); // 插入单词 "abcdg"
    cout << root->CountString("abcdg"); // 输出该单词在Trie中的数量
    cout << root->CountStringStartWith("abc"); // 输出以 "abc" 为前缀的单词数量
    root->Remove("abcdg"); // 删除单词 "abcdg"
    cout << root->CountString("abcdg"); // 输出该单词在Trie中的数量（此时应该为0，因为已删除）
}

对于Remove函数我最开始的的错误写法 

    void Remove(string str)
    {
        if(!CountString(str)) return;

        Trie* temp = root;
        int i;
        temp->pass --;

        for(auto it : str)
        {
            i = it - 'a';
            temp = temp->tries[i];
            if(!(-- temp->pass)) 
            {
                delete temp;
                temp = NULL;
                return;
            }
        }
        temp->end --;
    }

我认为的错误的原因：

比如在root之后的root->tries[i] 为 temp节点，temp的pass=1,那么把temp置为NULL,这样做不会的使得root->tries[i] = NULL的，其仍然指向一个明确的地址，只是temp被傻乎乎的置为NULL了。

2.使用数组实现树

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int Tree[1000][26];  // Trie 树的结构，最多1000个节点，每个节点有26个子节点（代表字母a-z）,值代表下一个节点是第几号
int End[1000];       // 用于标记某个节点是否是一个单词的结尾
int Pass[1000];      // 用于记录有多少个单词经过这个节点
int cnt = 0;         // 用于记录当前Trie树中的节点数量

void build() //初始化前缀树
{
    cnt = 1;         // 初始化Trie，根节点的编号为1
}

void Clear() //清空树
{
    memset(Tree, 0, sizeof(Tree));  // 清空Tree数组
    memset(End, 0, sizeof(End));    // 清空End数组
    memset(Pass, 0, sizeof(Pass));  // 清空Pass数组
    cnt = 0;                        // 重置节点计数器
}

void Insert(string str)//插入字符串
 {
    int cur = 1;     // 从根节点开始
    Pass[cur] ++;    // 根节点的通过数增加

    for(auto it : str) 
    {  // 遍历字符串中的每个字符
        int i = it - 'a';  // 将字符转化为索引值（0-25，对应a-z）
        if(!Tree[cur][i]) Tree[cur][i] = ++ cnt;  // 如果当前字符对应的子节点不存在，则创建新节点
        cur = Tree[cur][i];  // 移动到下一个节点
        Pass[cur] ++;        // 经过该节点的路径数加1
    }
    End[cur] ++;  // 标记该节点为单词的结尾
}

int CountString(string str)//计数字符串
 {
    int cur = 1;  // 从根节点开始
    for(auto it : str) {  // 遍历字符串中的每个字符
        int i = it - 'a';  // 将字符转化为索引值
        if(!Tree[cur][i]) return 0;  // 如果路径不存在，则单词不存在，返回0
        cur = Tree[cur][i];  // 移动到下一个节点
    }
    return End[cur];  // 返回该节点是否是单词的结尾，若是则返回对应的End值
}

void Remove(string str) //移除字符串
{
    if(!CountString(str)) return;  // 如果Trie中不存在这个单词，则直接返回

    int cur = 1;  // 从根节点开始
    Pass[cur] --;  // 根节点的通过数减少

    for(auto it : str) 
    {  // 遍历字符串中的每个字符
        int i = it - 'a';  // 将字符转化为索引值
        if(!(-- Pass[Tree[cur][i]])) 
        {  // 如果经过该节点的单词数减少到0，删除该路径
            Tree[cur][i] = 0;  // 该路径被清空
            return;
        }
        cur = Tree[cur][i];  // 移动到下一个节点
        Pass[cur] --;  // 经过该节点的路径数减少
    }

    End[cur] --;  // 该单词的结尾标记减少1
}

int CountStringStartWith(string str) //计数有几个字符串以str为前缀
{
    int cur = 1;  // 从根节点开始

    for(auto it : str) {  // 遍历字符串中的每个字符
        int i = it - 'a';  // 将字符转化为索引值
        if(!Tree[cur][i]) return 0;  // 如果路径不存在，则没有以该前缀开头的单词
        cur = Tree[cur][i];  // 移动到下一个节点
    }

    return Pass[cur];  // 返回以该前缀开头的单词数量
}

int main() 
{
    Insert("abcd");  // 插入单词 "abcd"
    cout << CountString("abcd");  // 输出单词 "abcd" 的计数
    cout << CountStringStartWith("abc");  // 输出以 "abc" 开头的单词数量

    Remove("abcd");  // 删除单词 "abcd"
    cout << CountString("abcd");  // 输出单词 "abcd" 的计数，应该为0
}

思路参考：算法讲解044【必备】前缀树原理和代码详解_哔哩哔哩_bilibili

18.一维差分和等差数列差分

一维差分:

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int arr[10];  // 定义一个长度为10的数组，初始值都为0，用于存储区间操作的结果

void f(int l, int r, int n) 
{
    arr[l] += n;        // 在索引为 l 的位置增加 n，表示从位置 l 开始增加 n
    arr[r + 1] -= n;    // 在索引为 r + 1 的位置减少 n，表示从位置 r+1 开始停止增加 n（这是差分的核心思想）

    for(int i = 1; i < 10; i++)  // 从索引 1 开始遍历数组
    {
        arr[i] += arr[i - 1];    // 通过前缀和的方式恢复实际数组
        cout << arr[i] << " ";   // 输出处理后的数组值
    }
}

int main() 
{
    int l, r, n;
    cin >> l >> r >> n;  // 输入区间 l, r 和增加的数值 n
    f(l, r, n);          // 调用函数 f 对区间 [l, r] 进行操作

}


等差数列差分：

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int arr[10];  // 定义一个长度为10的数组，初始值为0

// f 函数用于在给定区间 [l, r] 内根据初始值 s，结束值 e 和步长 d，更新数组
void f(int l, int r, int s, int e, int d) 
{
    arr[l] += s;             // 在 l 位置增加 s，表示从 l 开始的初始值为 s
    arr[l + 1] += d - s;     // 在 l+1 位置增加 d-s，用于设置第二个元素的差值
    arr[r + 1] -= d + e;     // 在 r+1 位置减去 d+e，保证从 r+1 位置开始影响结束

    // 第一次前缀和计算，基于差分数组累加每个元素
    for(int i = 1; i < 10; i++) 
        arr[i] += arr[i - 1];  // 对差分数组进行前缀和处理，恢复第一层变化

    // 第二次前缀和计算，累加上次计算结果，得到每个位置的实际值
    for(int i = 1; i < 10; i++) 
    {
        arr[i] += arr[i - 1];  // 再次累加，生成最终数组
        cout << arr[i] << " ";  // 输出结果数组中的元素
    }
}

int main() 
{
    int l, r, s, e, d;
    cin >> l >> r >> s >> e >> d;  // 输入区间 [l, r]，以及初始值 s，结束值 e 和步长 d
    f(l, r, s, e, d);              // 调用 f 函数，根据输入的值修改数组
}

19.短路（一种利用&&运算符特性的技巧）

class Solution {
public:
    int getSum(int n) {
        int res = n;
        (n > 0) && (res += getSum(n - 1));
        return res;
    }
};

(n > 0) && (res += getSum(n - 1));   一句就是短路

这句代码的原理利用了短路逻辑运算符 && 的特性。在这个表达式中：

  1. 条件判断：首先判断 n > 0。
  2. 短路特性：如果 n 为 0 或负数，&& 的左侧条件为 false，右侧的 getSum(n - 1) 不会被执行，从而终止递归。
  3. 递归调用：如果 n 大于 0，右侧的 getSum(n - 1) 会被调用，计算 n-1 的和，并将结果加到 res 中。

这种方式有效地控制了递归的终止条件，避免了不必要的函数调用。

20.质数筛（3种）

埃氏筛

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int f[90010], cnt, prime[90010]; //f -> 此数是否被标记为合数，否则仍为1，cnt计数质数个数,prime -> 存贮质数

void CountPrime(int n) // 定义 CountPrime 函数，参数 n 为需要计算素数的范围
{
    for(int i = 2; i * i <= n; i++) // 遍历 2 到 √n 之间的所有数 i
    {
        if(!f[i]) // 如果 f[i] 为 0，说明 i 是素数
        {
            for(int j = i * i; j <= n; j += i) // 从 i*i 开始，将 i 的倍数标记为非素数，步长为 i
            {
                if(!f[j]) // 如果 f[j] 还没被标记为非素数
                {
                    f[j] = 1; // 将 j 标记为非素数
                }
            }
        }
    }
    
    for(int i = 2; i <= n; i++) // 遍历 2 到 n 之间的所有数
    {
        if(!f[i]) cnt ++; //计数
    }

    cout << cnt; 
}

int main() 
{
    int x;
    cin >> x;
    CountPrime(x);
}

欧拉筛1（可以存储每个质数）

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int f[90010], cnt, prime[90010]; //f -> 此数是否被标记为合数，否则仍为1，cnt计数质数个数,prime -> 存贮质数

void CountPrime(int n) // 定义 CountPrime 函数，参数 n 为要筛选素数的范围
{
    for(int i = 2; i * i <= n; i++) // 从 2 开始遍历，筛选范围是 [2, √n]
    {
        if(!f[i]) prime[cnt++] = i; // 如果 f[i] 为 0，说明 i 是素数，将 i 存入 prime 数组，cnt 递增

        for(int j = 0; j < cnt; j++) // 遍历所有找到的素数 prime[j]
        {
            if(i * prime[j] > n) break; // 如果 i * prime[j] 大于 n，则退出循环，因为超出筛选范围
            f[i * prime[j]] = 1; // 将 i * prime[j] 标记为非素数
            if(i % prime[j] == 0) break; // 如果 i 是 prime[j] 的倍数，结束循环，以免重复标记
        }
    }

    cout << cnt; // 输出素数的数量
}


int main() 
{
    int x;
    cin >> x;
    CountPrime(x);
}

欧拉筛2（只计数版，不存储每个质数地值）

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

int f[90010], cnt; //f -> 此数是否被标记为合数，否则仍为1，cnt计数质数个数

void CountPrime(int n) // 定义 CountPrime 函数，参数 n 为需要计算素数的范围
{
    cnt = (n + 1) / 2; // 计算初始的素数计数，考虑到 2 是素数，其他奇数范围内的素数初始为 n/2

    for(int i = 3; i * i <= n; i += 2) // 从 3 开始，步长为 2，只检查奇数
    {
        if(!f[i]) // 如果 f[i] 为 0，说明 i 是素数
        {
            for(int j = i * i; j <= n; j += 2 * i) // 从 i*i 开始，标记 i 的倍数为非素数，步长为 2*i,如果步长是i,那么j会变成不需要判断的偶数
            {
                if(!f[j]) // 如果 f[j] 为 0，说明 j 还没有被标记为非素数
                {
                    f[j] = 1; // 标记 j 为非素数
                    cnt--; // 素数计数减一
                }
            }
        }
    }

    cout << cnt; // 输出素数的数量
}


int main() 
{
    int x;
    cin >> x;
    CountPrime(x);
}

思路参考：算法讲解097【必备】质数判断、质因子分解、质数筛_哔哩哔哩_bilibili

21.单调栈

此处展示了怎么存储数组中每一个值的前后最近的最小值，即维护一个单调递增的序列

#include<iostream> 
#include<algorithm> 
#include<string> 
#include<cstring> 
#include<stack> 
using namespace std;

int f[10010][2], a[10010]; // f数组存储最近小于元素的索引，a数组存储输入的数
int n; // 数组的大小

void MonotonicStack() // 单调栈函数
{
    stack<int> s; // 创建一个栈
    f[0][0] = -1; // 初始化第一个元素的左侧最近小于元素索引

    for(int i = 0; i < n; i ++) // 遍历数组,建立单调栈
    {
        while(!s.empty() && a[i] <= a[s.top()]) // 当栈不空且当前元素小于等于栈顶元素
        {
            int j = s.top(); // 获取栈顶索引
            s.pop(); // 弹出栈顶元素
            if(!s.empty()) f[j][0] = s.top(); // 更新左侧最近小于元素索引
            else f[j][0] = -1; // 如果栈空，则设为-1
            f[j][1] = i; // 更新右侧最近小于元素索引
        }   
        s.push(i); // 将当前索引压入栈
    }

    int t = s.size(); // 获取栈的大小
    while(t) // 处理栈中剩余元素
    {
        if(t > 1) // 如果栈中还有多个元素
        {
            int tmp = s.top(); // 获取栈顶索引
            s.pop(); // 弹出栈顶元素
            f[tmp][0] = s.top(); // 更新左侧最近小于元素索引
            f[tmp][1] = -1; // 右侧设为-1
        }
        else f[s.top()][0] = f[s.top()][1] = -1; // 只有一个元素，左右均设为-1
        t --; // 递减计数
    }

    for(int i = n - 1; i >= 0; i --) // 从后往前遍历单调栈，防止有相同的值是最小左值
    {
        if(a[f[i][1]] == a[i]) f[i][1] = f[f[i][1]][1]; // 如果右侧最近小于元素相等，则更新
    }

    for(int i = 0; i < n; i ++) cout << i << ": " << f[i][0] << " " << f[i][1] << endl; // 输出结果
}

int main() 
{
    cin >> n; 
    for(int i = 0; i < n; i ++) cin >> a[i]; 
    MonotonicStack(); 
}

思路参考：算法讲解052【必备】单调栈-上_哔哩哔哩_bilibili

22.博弈论（6类基础博弈）

1.巴什博弈

2.巴什博弈拓展

3.尼姆博弈

4.反尼姆博弈

5.斐波那契博弈

6.威佐夫博弈

思路参考：算法讲解095【必备】博弈类问题必备内容详解-上_哔哩哔哩_bilibili

一款CTF杂项利器(支持36种常见编码和密码算法的加密和解密，31种密文的分析和识别，支持自动提取flag，自定义插件等).zip
02-18
一款CTF杂项利器(支持36种常见编码和密码算法的加密和解密，31种密文的分析和识别，支持自动提取flag，自定义插件等).zip 一款CTF杂项利器(支持36种常见编码和密码算法的加密和解密，31种密文的分析和识别，支持自动...
cpp-图论算法最小生成树Prim算法和Kruskal算法C实现
08-16
在计算机科学领域，图论算法是解决复杂问题的重要工具，特别是在网络优化、数据结构和算法设计上。最小生成树（Minimum Spanning Tree, MST）问题就是其中之一，它旨在找到一个加权无向图中的边子集，使得这些边连接...
算法基础杂项
CUITAO2305532402的博客
03-14 432
1.首先，保证时间复杂度最低。2.其次，保证空间复杂度最低。3.常数项低不低，一般没人管。
算法杂项
chenpeng19910926的专栏
01-17 265
简单介绍一下包含的内容： 动态规划题： ♥问题一：最低消耗问题      ♥问题二：生小牛的故事 ♥♥问题三：计算有多少种最长的递增序列 ♥♥问题四：给数字N，以1...N为节点能构建多少颗不同二叉搜索树 ♥♥问题五：矩阵连乘 ♥♥♥问题七：凸多边形最优三角剖分 字符串相关题： ♥问题一：字符串匹配求两个字符串的最大公共连续子串 ♥问题二：基本计算器 ♥♥问题三：字符串匹配有哪些...
Mess 杂项算法
千淘万漉虽辛苦，吹尽狂沙始到金
10-19 224
Mess 杂项算法 Q_read/Q_write inline int qr(){ int x = 0, f = 1; char c = getchar(); while(!isdigit(c)) { if(c == '-') f = -f; c = getchar(); } while(isdigit(c)) { x = (x << 1) + (x << 3) + (c ^ 48);
算法竞赛中的杂项算法
idio_dsfrbeki的博客
09-25 1529
持续更新中喔~~~，如果有错误欢迎提出噢^_^。
11、编程中的杂项与排序算法解析
i8j9k0l1的博客
08-31 30
本博客深入解析了编程中的多种杂项代码和排序算法，涵盖了逻辑运算、对数计算、信号平滑、最大公约数计算、伪随机数生成、暴力算法、字母检测以及矩阵字母检测等内容。同时详细介绍了不同排序算法的实现原理、应用场景及复杂度分析，帮助读者根据实际问题选择合适的算法和代码实现。
算法基础 篇1(杂项)
qq_73944088的博客
05-04 596
2.万能头文件（包含很多用到的函数） 3.取消同步流(可以加速cin,cout带来的影响) 4.c++保留小数位 5.c++新定义 6.快速计算星期几(由年月日算是周几) 7.bool类型 bool类型有两个输出值:true(代表1，代表真)false(代表0，代表假) 8.读入带空格的字符串 9.一些容器(后面结合数据结构陆续整理出来) vector:动态数组容器pair:一对值的组合set:存储不重复元素，集合map:关联容器，存键值对queue:
【算法讲解】杂项算法——异或哈希(xor-hashing)
notonlysuccess的博客
06-01 9456
异或哈希是个很神奇的算法，利用了异或操作的特殊性和哈希降低冲突的原理，可以用于快速找到一个组合是否出现、序列中的数是否出现了k次
CTF杂项一
2302_80189643的博客
05-27 944
扫描后得到\u7f8a\u7531\u5927\u4e95\u592b\u5927\u4eba\u738b\u4e2d\u5de5，使用在线工具unicode解码，得到中文‘羊由大井夫大人王中工’，当铺密码，解密后得到9158753624，提交flag后发现不正确。小明是个特工，之前的每次接头都会多多少少的会跟敌人有正面冲突，于是小明下决心要做一个黑阔，他找到一位德高望重的大黑客。题目描述：光辉岁月，我是一个女生，天生对数学部明干，少年时我从未考虑过哥德巴赫猜想，大学学多元。发现可疑人物，证明了猜想。
LeetCode算法---题型总纲之杂项算法
SOLar7SysteM的博客
03-17 450
LeetCode算法—题型总纲之杂项算法 杂项算法 杂项算法 标题预处理 随机算法 水塘抽样 拒绝采样 离散化 高精度 模拟 博弈 扫描线 状态压缩 脑筋急转弯 交互
2025年全国青少年信息素养大赛复赛真题（算法创意实践挑战赛C++初中组试卷1：带解析）（7月6日试卷）
王老师青少年编程
11-21 718
2025年全国青少年信息素养大赛复赛真题（算法创意实践挑战赛C++初中组试卷1：带解析）（7月6日试卷）
代码随想录 63.不同路径Ⅱ
m0_63814538的博客
11-24 281
4.确定遍历顺序：从递归公式可以看出一定是从左到右一层一层的遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j]和dp[i][j - 1]一定是有数值的。所以本题的初始化代码如下所示：一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理。1.确定dp数组（dp table）及其下标的含义：dp[i][j]表示从（0，0）出发，到（i，j）有dp[i][j]条不同的路径。下标（0，j）的初始化情况同理。
【Python TensorFlow】 TCN-LSTM时间序列卷积长短期记忆神经网络时序预测算法（附代码）
q22837656的博客
11-24 297
本文提出了一种结合时间卷积网络(TCN)和长短期记忆网络(LSTM)的混合预测算法(TCN-LSTM)，用于解决传统时间序列预测方法在捕捉长期依赖和局部特征方面的不足。该算法利用TCN的并行计算能力和LSTM的序列建模优势，通过五步流程实现：数据准备、预处理、网络构建、模型训练和评估。代码示例展示了数据读取、特征提取、归一化处理及模型训练过程，支持多种输入输出模式。实验结果表明，该混合模型能有效提升时序预测性能，适用于电力负荷、风电场功率等多种应用场景。
算法：二叉搜索树的最近公共祖先
czlczl20020925的博客
11-24 340
下面是详细的解释，说明为什么这是必然的。对于我们当前所在的任何节点。
算法沉淀第十二天（牛客练习赛146）
lingran__的博客
11-22 820
本文分享了牛客练习赛146的三道算法题解：1.《合格的机器》通过分析代币奇偶性，得出最优解是尽量使机器代币数为偶数，当总代币数≥2n时最多n-1台合格；2.《小灰灰的火焰星球2》通过排序施法顺序和预处理价值数组，实现高效计算最大收益；3.《盲目自大的小灰灰》通过计算得分区间，判断查询分数是否可能达到。每道题都包含题意分析、逻辑梳理和AC代码实现，适合算法学习者参考。
【元启发算法】模拟退火（SA）：在温度起伏中，寻找最优解的诗意算法
Harrytutu_ZuiYue的博客
11-21 373
自然从不急于求成，金属在冷热交替中趋于稳定，算法亦在温度起落中逼近真理。” 寒冬里调温的空调、背包旅行时规划路线、手机 APP 优化资源分配 —— 生活中处处藏着 “寻找最优解” 的难题。有些问题看似简单，却因可选方案过多，让我们陷入 “局部最优” 的困境：就像在山谷中徒步，误以为眼前的山峰就是最高点，却不知翻过一座小山后，还有更广阔的天地。
算法基础篇：（十六）深度优先搜索（DFS）之递归型枚举与回溯剪枝初识
最新发布
2301_79248256的博客
11-24 452
本文聚焦深度优先搜索（DFS）的递归型枚举与回溯剪枝，以枚举子集、组合型枚举、枚举排列、全排列四个洛谷经典例题为切入点，从问题描述、决策树分析、递归函数设计到代码实现逐步拆解。先阐释搜索本质及 DFS 与回溯、剪枝的关联，再通过具体案例讲解回溯的 “恢复现场” 操作与可行性、重复性等剪枝技巧，总结 DFS 递归型枚举 “画决策树 - 设计函数 - 实现回溯 - 添加剪枝” 的通用步骤，帮助读者理解并掌握 DFS 解决枚举类问题的核心方法，为进阶应用奠定基础。
LeetCode算法解题杂项第四篇
在线选举问题是一个典型的编程问题，通常出现在各类算法竞赛和面试中。它涉及到数据结构的应用，特别是用于查找和更新数据。 **核心概念** 在在线选举问题中，假设有多个候选人竞选某个职位，每位候选人都有一个...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值