The Optimization of the Adaboost and Gradient Boosted Decision Tree...

The Optimization of the Adaboost

1.对于Adaboost error function的推导

再回到我们上篇文章讲到的Adaboost算法，我们要从Adaboost算法推导出GBDT。首先回顾一下上篇文章的Adaboost，主要思想就是把弱分类器集中起来得到一个强的分类器。首先第一次建造树的时候每一个样本的权值都是一样的，之后的每一次训练只要有错误，那么这个错误就会被放大，而正确的权值就会被缩小，之后会得到每一个模型的α，根据每一个树的α把结果结合起来就得到需要的结果。

在Adaboost里面，Ein表达式：

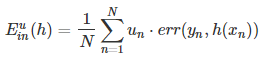
每一个错误的点乘权值相加求平均，我们想把这一个特征结合到decision tree里面，那么就需要我们在决策树的每一个分支下面加上权值，这样很麻烦。为了保持决策树的封闭性和稳定性，我们不改变结构，只是改变数据的结果，喂给的数据乘上权值，其他的不改变，把决策树当成是一个黑盒子。
权值u其实就是这个数据用boostrap抽样抽到的概率，可以做一个带权抽样，也就是带了u的sample，这样抽出来的数据没一个样本和u的比例应该是差不多一致的，所以带权sampling也叫boostrap的反操作。这种方法就是对数据本身进行改变而对于算法本身的数据结构不变。

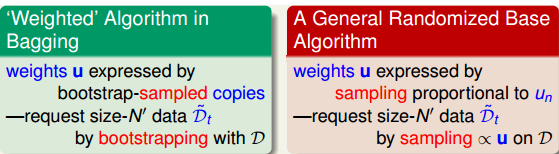
上面的步骤就是得到gt，接下来就是求α了，α就是每一个model的重要性，上节课我们是讲到过怎么求的，先得到错误率ξ，然后：

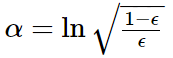
这个东西很重要，之后我们会对这公式做推导。

①为什么Adaboost要弱类型的分类器？
分类器讲道理，应该是越强越好的，但是Adaboost相反，他只要弱的，强的不行。来看一下α，如果你的分类器很强，ξ基本就是equal 0了，这样的α是无穷大的，其他的分类器就没有意义了，这样就又回到了单分类器，而单分类器是做不到aggregation model的好处的，祥见aggregation model这篇文章。

我们把这种称为autocracy，独裁。针对这两个原因，我们可以做剪枝，限制树的大小等等的操作，比如只使用一部分样本，这在sampling的操作中已经起到这类作用，因为必然有些样本没有被采样到。

所以，综上原因，Adaboost常用的模型就是decision stump，一层的决策树。

事实上，如果树高为1时，通常较难遇到ξ=0的情况，且一般不采用sampling的操作，而是直接将权重u代入到算法中。这是因为此时的AdaBoost-DTree就相当于是AdaBoost-Stump，而AdaBoost-Stump就是直接使用u来优化模型的。前面的算法实现也是基于这些理论实现的算法。

回到正题，继续从optimization的角度讨论Adaboost，Adaboost权重计算如下：

把上面两张形式结合一下，得到下面综合形式。第一层的u是1/N，每一次递推要乘上

于是，u(t+1)：

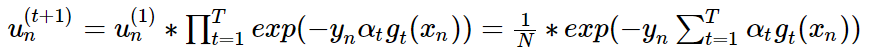
而在这里面

称为是voting score，也就是集合投票的分数，而u(t+1)是和voting score成正比的：

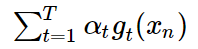
仔细看一下，voting score是由许多的g(x)通过不同的α进行线性组合而成的，换一个角度，把g(x)看做是特征转换的φ(x)，α就是权重w，这样一来再和SVM对比一下：

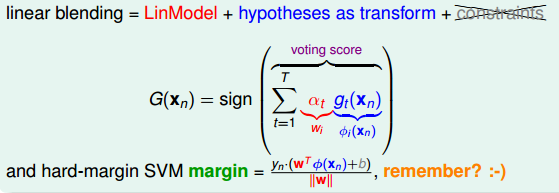
对比上面其实是很像的，乘上的y就是表名是在正确的一侧还是错误的一侧，所以，这里的voting score也可以看做是没有正规化的距离。也就是没有除|w|的距离，所以从效果上看，voting score是要越大越好。再来看之前的乘上y的表达式，我们要做的就是要使得分类正确，所以y的符号和voting score符号相同的数量会越来越多，这样也就保证了这个voting score是在不断增大，距离不断增大。这种距离要求大的在SVM里面我们叫正则化——regularization，同样，这样就证明了①Adaboost的regularization。刚刚的g(x)看做是φ其实就是feature transform，所以也证明了②Adaboost的feature transform。这两个特性一个是踩刹车一个是加速，效果固然是比单分类器好的。

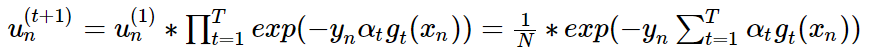
所以根据上面的公式，可以得到u是在不断减小的：

所以我们的目标就是要求经过了(t+1)轮的迭代之后，u的数据集合要越来越小。有如下：

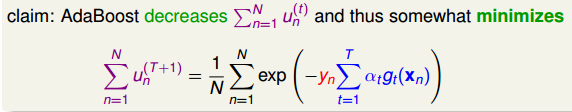
②Adaboost的error
上式中我们把voting score看做是s。对于0/1error，如果ys >= 0，证明是分类正确的，不惩罚err0/1 = 0,；如果ys < 0，证明分类错误，惩罚err0/1 = 1。对于Adaboost，我们可以用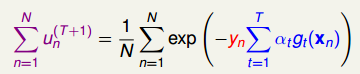

来表示，可能有些同学觉得这里不太对， 这里明明是u的表达式为什么可以作为错误的衡量？这个表达式里面包含了y和s，正好可以用来表达Adaboost的error，是就使用了。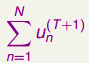

正好也是减小的，和我们需要的err是一样的，要注意这里Adaboost我们是反推，已知到效果和方法反推表达式，使用要用上一切可以使用的。
和error0/1对比：

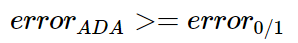
所以，Adaboost的error function是可以代替error0/1的，并且效果更好。

2.对于Adaboost error function的一些简单处理

③首先要了解一些泰勒展开：
在一般的函数情况下，是有: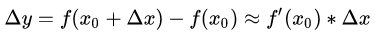

①：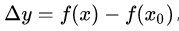

②：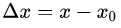

①②式子代入上面：

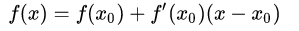
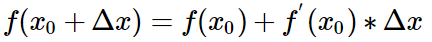
这就是一阶Taylor expansion。待会要利用他们来求解。

用Taylor expansion处理一下Adaboost error function：

这是Gradient descent的公式，我们类比一下error function：

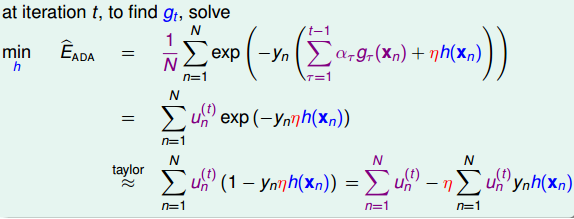
这里是使用exp(x) 的Taylor一阶展开，这里的方向是h(x)，而Gradient descent是w才是方向，w是某一个点的方向，而h(x)也可以代入某一个点得到一个value，这个value就是方向，所以基本上和梯度下降是一致的：

以上的对于error function的分解是在x = 0的点进行Taylor展开，可以看到前面的一项是常数，后面的一项才是变量，使用我们需要优化的就是减小后面一项的值。所以我们先要找到一个最合适的h(x)来优化这个函数，n先忽略：

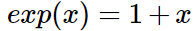
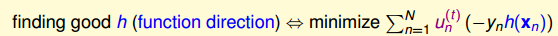
对于y和h(x)我们均限定是{1，-1}，对这个优化项做一些平移：

所以要优化的项最后又转变成了Ein，我们的演算法一直都是在做减小Ein这件事，所以Adaboost的base algorithm——decision stump就是做的这件事。h(x)就可以解决了。

解决了h(x)的问题接下来就是η的问题了：

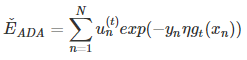
所以最后的公式如上图所示。
上式中有几个情况可以考虑：

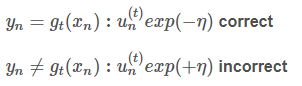
经过推导：

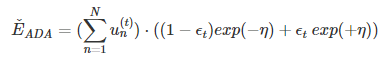
求η最小值自然就是求导了：

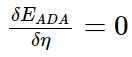
就得到：

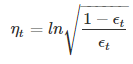
而η = α，这样就推导出了α的表达式了。
Adaboost实际上就是在寻找最块下降方向和最快下降步长的过程中优化，而α相当于最大的步长，h(x)相当于最快的方向。所以，Adaboost就是在Gradient descent上寻找最快的方向和最快的步长。

Gradient Boosted Decision Tree

推导完了Adaboost，我们接着推导Gradient Boosted Decision Tree，其实看名字就知道只不过是error function不太一样而已。前面Adaboost的推导总的可以概括为：

这种exp(-ys)function是Adaboost专有的，我们能不能换成其他的？比如logistics或者linear regression的。

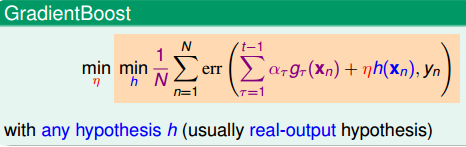
使用Gradient descent的就是这种形式，虽然形式变了，但是最终的结果都是求解最快的方向和最长的步长。

这里使用均方差替代error。使用一阶泰勒展开：

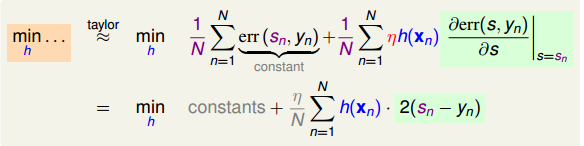
constant我们不需要管，我们只需要关心最后的一项。使得这一项最小，那只需要h(x)和2(s - y)互为相反数，并且h(x)很大很大就好了，h(x)不做限制，很明显这样是求不出来的。有一个简单的做法，收了regularization的启发，我们可以在后面加上惩罚项，使用L2范式，L2范式会使他们很小但不会为0，但是L1范式会使得他们集中到边角上，系数矩阵，使用这里使用L2范式，另一方面，也是对于化简的方便做了准备。

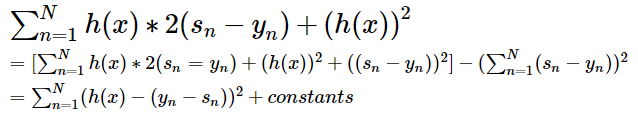
所以，优化的目标：

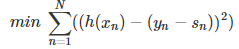
y-s我们称为残差，我们要做的就是使得h(x)和(y - s)接近，也就是做一个拟合的过程，也就是做regression。

拟合出来得到的h(x)就是我们要的gt(x)了。之后就是求η了。
③：

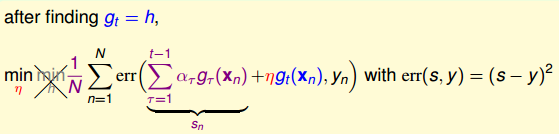
得到了g(x)之后就是求η步长了。注意上面的③才是我们要求的公式，

这一个知识为了化简方便的。

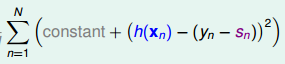
总结一下，以上就是GBDT的流程了。值得注意的是，sn的初始值一般均设为0，即s1=s2=⋯=sN=0。每轮迭代中，方向函数gt通过C&RT算法做regression，进行求解；步进长度η通过简单的单参数线性回归进行求解；然后每轮更新sn的值，即sn←sn+αtgt(xn)。T轮迭代结束后，最终得到

。值得一提的是，本节课第一部分介绍的AdaBoost-DTree是解决binary classification问题，而此处介绍的GBDT是解决regression问题。二者具有一定的相似性，可以说GBDT就是AdaBoost-DTree的regression版本。

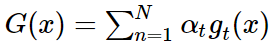
Summary of Aggregation Models

到这里，aggregation model基本就完成了。主要有三个方面：
①uniform：把g(x)平均结合。
②non-uniform：把g(x)线性组合。
③conditional：根据不同条件做非线性组合。
uniform采用投票、求平均的形式更注重稳定性；而non-uniform和conditional追求的更复杂准确的模型，但存在过拟合的危险。

刚刚所讨论的model都是建立在g(x)已知的情况下，如果g(x)不知道，我们就可以使用一下方法：
①Bagging：通过boostrap方法训练模型平均结合结果。
②Adaboost：通过boostrap方法训练模型进行线性组合。
③Decision Tree：数据分割得到不同的g(x)进行线性组合。

除了以上的方法，我们还可以把Bagging和Decision Tree结合起来称为random forest，Adaboost和decision tree结合起来就是Adaboost-stump，Gradient Boosted和Adaboost结合起来就是GBDT了。

Aggregation的核心是将所有的gt结合起来，融合到一起，也就是集体智慧的思想。这种做法能够得到好的G的原因，是因为aggregation具有两个方面的优点：cure underfitting和cure overfitting。
①aggregation models有助于防止欠拟合（underfitting）。它把所有比较弱的gt结合起来，利用集体智慧来获得比较好的模型G。aggregation就相当于是feature transform，来获得复杂的学习模型。
②aggregation models有助于防止过拟合（overfitting）。它把所有gt进行组合，容易得到一个比较中庸的模型，类似于SVM的large margin一样的效果，避免了一些过拟合的情况发生。从这个角度来说，aggregation起到了regularization的效果。
由于aggregation具有这两个方面的优点，所以在实际应用中aggregation models都有很好的表现。

代码实现

主要的做法就是用{(x, (y - s))}做拟合就好了。
由于之前写的决策树结构设计的不太好，使用起来不方便于是重新写了一个，这里的CART树是用方差来衡量impurity的。

def loadDataSet(filename):
    '''
    load dataSet
    :param filename: the filename which you need to open
    :return: dataset in file
    '''
    dataMat = pd.read_csv(filename)
    for i in range(np.shape(dataMat)[0]):
        if dataMat.iloc[i, 2] == 0:
            dataMat.iloc[i, 2] = -1
    return dataMat
    pass

def split_data(data_array, col, value):
    '''split the data according to the feature'''
    array_1 = data_array.loc[data_array.iloc[:, col] >= value, :]
    array_2 = data_array.loc[data_array.iloc[:, col] < value, :]
    return array_1, array_2
    pass

def getErr(data_array):
    '''calculate the var '''
    return np.var(data_array.iloc[:, -1]) * data_array.shape[0]
    pass

def regLeaf(data_array):
    return np.mean(data_array.iloc[:, -1])

加载数据，分割数据，计算方差，计算叶子平均,其实就是计算拟合的类别了。

def get_best_split(data_array, ops = (1, 4)):
    '''the best point to split data'''
    tols = ops[0]
    toln = ops[1]
    if len(set(data_array.iloc[:, -1])) == 1:
        return None, regLeaf(data_array)
    m, n = data_array.shape
    best_S = np.inf
    best_col = 0
    best_value = 0
    S = getErr(data_array)
    for col in range(n - 1):
        values = set(data_array.iloc[:, col])
        for value in values:
            array_1, array_2 = split_data(data_array, col, value)
            if (array_1.shape[0] < toln) or (array_2.shape[0] < toln):
                continue
            totalError = getErr(array_1) + getErr(array_2)
            if totalError< best_S:
                best_col = col
                best_value = value
                best_S = totalError
    if (S - best_S) < tols:
        return None, regLeaf(data_array)
    array_1, array_2 = split_data(data_array, best_col, best_value)
    if (array_1.shape[0] < toln) or (array_2.shape[0] < toln):
        return None, regLeaf(data_array)

    return best_col, best_value

得到最好的分类，这里相比之前的决策树加了一些条件限制，叶子数量不能少于4，和之前的一样，计算方差对比看看哪个小。

class node:
    '''tree node'''
    def __init__(self, col=-1, value=None, results=None, gb=None, lb=None):
        self.col = col
        self.value = value
        self.results = results
        self.gb = gb
        self.lb = lb
        pass

叶子节点，col列，val划分的值，results结果，gb右子树，lb左子树。

def buildTree(data_array, ops = (1, 4)):
    col, val = get_best_split(data_array, ops)
    if col == None:
        return node(results=val)
    else:
        array_1, array_2 = split_data(data_array, col, val)
        greater_branch = buildTree(array_1, ops)
        less_branch = buildTree(array_2, ops)
        return node(col=col, value=val, gb=greater_branch, lb=less_branch)
    pass

建立一棵树。

def treeCast(tree, inData):
    '''get the classification'''
    if tree.results != None:
        return tree.results
    if inData.iloc[tree.col] > tree.value:
        return treeCast(tree.gb, inData)
    else:
        return treeCast(tree.lb, inData)
    pass

def createForeCast(tree, testData):
    m = len(testData)
    yHat = np.mat(np.zeros((m, 1)))
    for i in range(m):
        yHat[i, 0] = treeCast(tree, testData.iloc[i])
    return yHat

创建分类。

def GBDT_model(data_array, num_iter, ops = (1, 4)):
    m, n = data_array.shape
    x = data_array.iloc[:, 0:-1]
    y = data_array.iloc[:, -1]
    y = np.mat(y).T
    list_trees = []
    yHat = None
    for i in range(num_iter):
        print('the ', i, ' tree')
        if i == 0:
            tree = buildTree(data_array, ops)
            list_trees.append(tree)
            yHat = createForeCast(tree, x)
        else:
            r = y - yHat
            data_array = np.hstack((x, r))
            data_array = pd.DataFrame(data_array)
            tree = buildTree(data_array, ops)
            list_trees.append(tree)
            rHat = createForeCast(tree, x)
            yHat = yHat + rHat
    return list_trees, yHat

这里只是使用了回归问题的回归树，x和(y - s)做拟合之后加入预测集即可。
接下来就是画图了：

def getwidth(tree):
    if tree.gb == None and tree.lb == None: return 1
    return getwidth(tree.gb) + getwidth(tree.lb)


def getdepth(tree):
    if tree.gb == None and tree.lb == None: return 0
    return max(getdepth(tree.gb), getdepth(tree.lb)) + 1


def drawtree(tree, jpeg='tree.jpg'):
    w = getwidth(tree) * 100
    h = getdepth(tree) * 100 + 120

    img = Image.new('RGB', (w, h), (255, 255, 255))
    draw = ImageDraw.Draw(img)

    drawnode(draw, tree, w / 2, 20)
    img.save(jpeg, 'JPEG')


def drawnode(draw, tree, x, y):
    if tree.results == None:
        # Get the width of each branch
        w1 = getwidth(tree.lb) * 100
        w2 = getwidth(tree.gb) * 100

        # Determine the total space required by this node
        left = x - (w1 + w2) / 2
        right = x + (w1 + w2) / 2

        # Draw the condition string
        draw.text((x - 20, y - 10), str(tree.col) + ':' + str(tree.value), (0, 0, 0))

        # Draw links to the branches
        draw.line((x, y, left + w1 / 2, y + 100), fill=(255, 0, 0))
        draw.line((x, y, right - w2 / 2, y + 100), fill=(255, 0, 0))

        # Draw the branch nodes
        drawnode(draw, tree.lb, left + w1 / 2, y + 100)
        drawnode(draw, tree.gb, right - w2 / 2, y + 100)
    else:
        txt = str(tree.results)
        draw.text((x - 20, y), txt, (0, 0, 0))

之后就是运行主函数了：

if __name__ == '__main__':
    data = loadDataSet('../Data/LogiReg_data.txt')
    tree = buildTree(data)
    drawtree(tree, jpeg='treeview_cart.jpg')
    gbdt_results, y = GBDT_model(data, 10)
    print(y)
    for i in range(len(y)):
        if y[i] > 0:
            print('1')
        elif y[i] < 0:
            print('0')

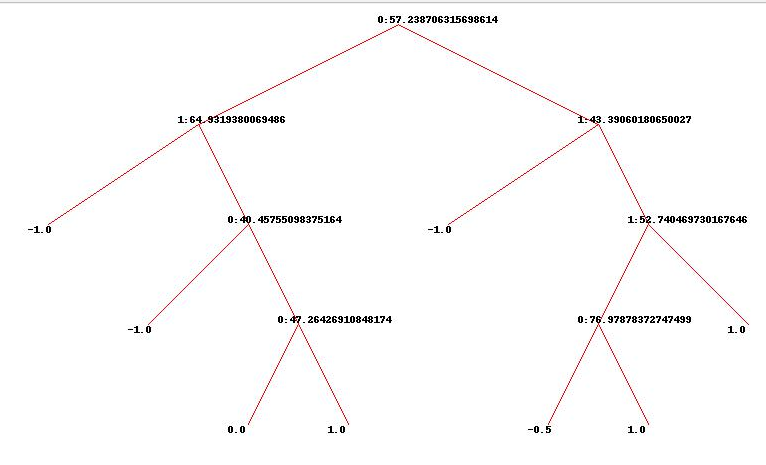
效果：

效果貌似还是可以的。aggregation model就到此为止了，几乎所有常用模型都讲完了。

最后符上GitHub所有代码：
https://github.com/GreenArrow2017/MachineLearning/tree/master/MachineLearning/GBDT