机器学习入门与经典knn算法表文解析-优快云博客

本文链接：https://blog.youkuaiyun.com/cpluspluszz/article/details/149614780

在数字化浪潮席卷全球的今天，机器学习已成为驱动科技创新的核心动力之一。它能从海量数据中挖掘潜在规律，为各行各业提供智能化解决方案 —— 从电商平台的个性化推荐，到医疗领域的疾病早期诊断，再到交通系统的智能调度，机器学习的应用场景无处不在。理解机器学习的基本逻辑，掌握经典算法的使用方法，已成为当代技术从业者的必备技能。

一、机器学习基础框架

机器学习是人工智能的核心分支，其本质是让计算机通过数据自主学习规律，而非依赖人工编写的固定规则。根据学习模式的差异，可分为三大类：

学习方式	核心特点	主要任务	应用示例
监督学习	训练数据包含输入特征和对应的标签（已知答案），算法构建输入到输出的映射关系	分类任务：将数据划分到离散的类别中	邮件系统识别垃圾邮件；银行判断贷款申请是否存在违约风险
		回归任务：预测连续的数值型结果	房地产平台预测房屋市场价格；气象部门预测未来几天的气温变化
无监督学习	处理无标签数据，算法自主发现数据中隐藏的结构和模式	聚类任务：将相似的样本自动归为一类	电商平台对用户进行分群以制定营销策略；生物学家通过基因序列数据聚类发现物种间进化关系
		降维任务：在保留核心信息的前提下减少特征维度	在图像识别中对高分辨率图像的像素特征降维，加快计算速度并去除冗余信息
强化学习	通过 “试错” 机制让智能体与环境交互，学习最优策略，目标是最大化长期累积奖励	无明确细分任务，以学习最优行为策略为主	AlphaGo 通过与自己对弈学习围棋最优落子策略；自动驾驶汽车在模拟环境中优化转向、加速、刹车等操作

二，KNN 算法深度解析

KNN（K 近邻算法）是机器学习中最直观的算法之一，属于监督学习中的实例 - based 方法。它不依赖复杂的数学模型，而是通过 “相似性” 判断来进行预测，非常适合入门学习。

核心原理

KNN 的核心思想源于生活中的 “物以类聚，人以群分”——一个样本的类别，由其周围最相似的 K 个样本（近邻）的多数类别决定。例如，在判断一朵未知花的品种时，若它周围最近的 3 朵花都是 “鸢尾花”，那么这朵花大概率也是鸢尾花。

完整执行步骤

数据准备：收集带特征和标签的训练数据（如不同花的花瓣长度、宽度及对应的品种），并确定待预测的新样本。

距离计算：衡量样本间相似性的关键步骤，常用的距离度量方法有：

距离度量方法	适用场景	计算公式（以二维空间为例）	特点
欧式距离	连续型特征	$\sqrt{(x1-x2)^2 + (y1-y2)^2}$	最经典的距离计算方式，能反映两点在空间中的直线距离
曼哈顿距离	网格状数据（如城市道路导航）	$	x1-x2
余弦相似度	文本、图像等向量数据	$\cos\theta=\frac{x1x2 + y1y2}{\sqrt{x1^2 + y1^2}\cdot\sqrt{x2^2 + y2^2}}$	衡量两个向量方向的一致性，值越接近 1 则越相似，忽略向量绝对大小

筛选近邻：计算新样本与所有训练样本的距离后，按距离从小到大排序，选取前 K 个样本作为近邻。
投票决策：统计 K 个近邻的类别，出现次数最多的类别即为新样本的预测类别（分类任务）；若为回归任务，则取 K 个近邻的平均值作为预测结果。

K 值选择策略

K 值的选取直接影响模型性能，需结合数据特点合理设置：

K 值过小：模型易受噪声数据影响，出现过拟合（如 K=1 时，单个异常样本可能导致预测错误）。

K 值过大：近邻中可能包含大量无关样本，导致模型欠拟合，无法捕捉数据的局部特征。

实践技巧：通常选择奇数（如 3、5、7）以避免投票平局；通过交叉验证（如将数据分为 5 份，轮流用 4 份训练、1 份验证）找到最优 K 值，使模型在验证集上的准确率最高。

算法优缺点剖析

优势

简单易用：原理直观，实现难度低，无需复杂的参数调优，适合初学者上手。

适应性强：可直接处理多分类问题，无需额外调整算法结构。

动态学习：作为惰性学习算法，无需预训练模型，新增数据可直接加入训练集，无需重新训练。

局限

计算成本高：预测时需与所有训练样本计算距离，当数据量达到百万级时，计算速度会显著下降。

对数据分布敏感：若训练集中某类样本占比过高（如 90%），即使新样本更接近少数类，也可能被误判为多数类。

维度灾难：当特征维度极高（如文本的词向量维度），距离度量的区分度会大幅降低，导致模型失效。

三，KNN 算法代码实战

以下通过鸢尾花数据集（包含 3 种鸢尾花的花瓣、花萼尺寸特征），演示 KNN 分类的完整实现过程。

代码实现(可复制到本地运行查看）：

# 导入必要的库

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split, cross_val_score

from sklearn.neighbors import KNeighborsClassifier

from sklearn.metrics import accuracy_score, classification_report

import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif'] = ['SimSun']

plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题
# 1. 加载数据集

iris = load_iris()

X = iris.data # 特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度

y = iris.target # 标签：0-山鸢尾，1-变色鸢尾，2-维吉尼亚鸢尾

feature_names = iris.feature_names

target_names = iris.target_names

# 2. 划分训练集与测试集（7:3）

X_train, X_test, y_train, y_test = train_test_split(

X, y, test_size=0.3, random_state=42 # random_state确保结果可复现

)

# 3. 构建KNN模型并优化K值

# 尝试不同K值，通过交叉验证选择最优值

k_range = range(1, 21)

cv_scores = []

for k in k_range:

knn = KNeighborsClassifier(n_neighbors=k)

# 5折交叉验证，计算平均准确率

scores = cross_val_score(knn, X_train, y_train, cv=5, scoring='accuracy')

cv_scores.append(scores.mean())

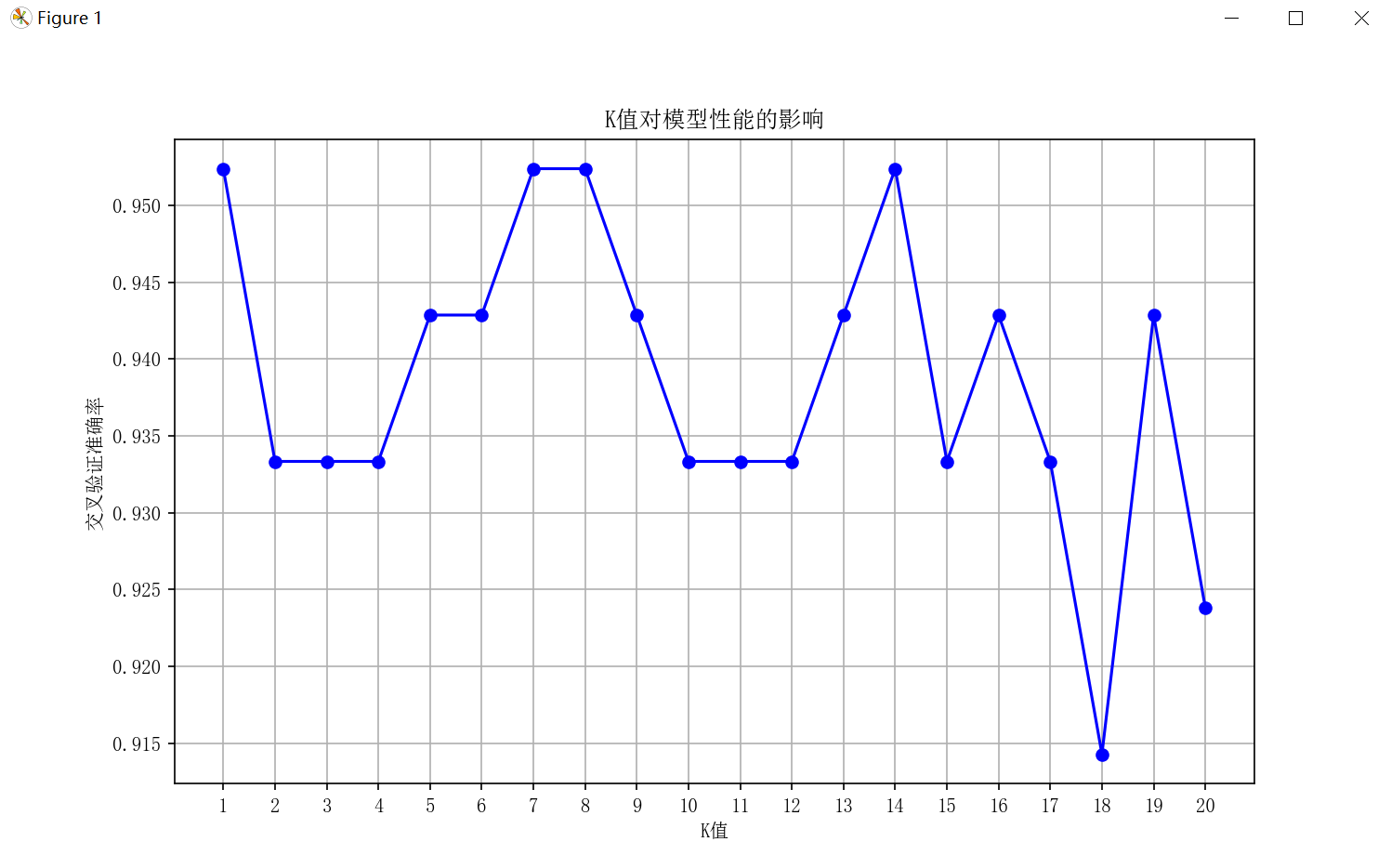
# 可视化不同K值的交叉验证准确率

plt.figure(figsize=(10, 6))

plt.plot(k_range, cv_scores, marker='o', color='b')

plt.xlabel('K值')

plt.ylabel('交叉验证准确率')

plt.title('K值对模型性能的影响')

plt.xticks(k_range)

plt.grid(True)

plt.show()

# 选择最优K值（准确率最高的K）

best_k = k_range[cv_scores.index(max(cv_scores))]

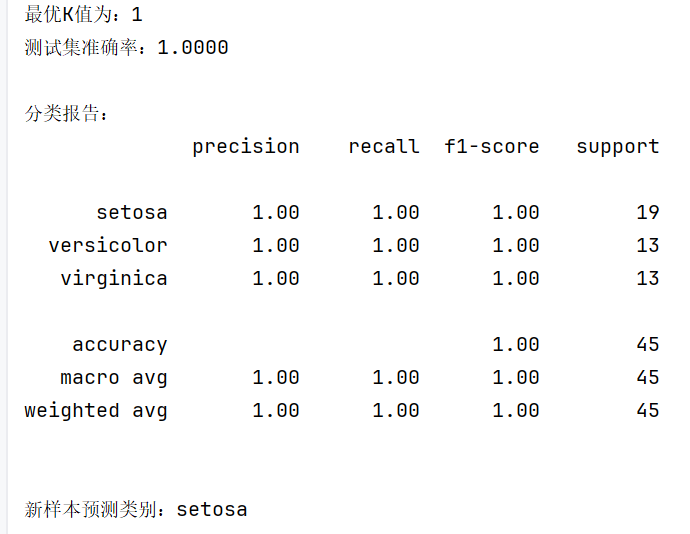
print(f'最优K值为：{best_k}')

# 4. 用最优K值训练模型并评估

best_knn = KNeighborsClassifier(n_neighbors=best_k)

best_knn.fit(X_train, y_train) # KNN的fit仅存储训练数据

# 预测测试集

y_pred = best_knn.predict(X_test)

# 评估模型性能

print(f'测试集准确率：{accuracy_score(y_test, y_pred):.4f}')

print('\n分类报告：')

print(classification_report(y_test, y_pred, target_names=target_names))

# 5. 预测新样本

# 假设新样本特征：花萼长5.0，花萼宽3.6，花瓣长1.4，花瓣宽0.2

new_sample = [[5.0, 3.6, 1.4, 0.2]]

predicted_class = best_knn.predict(new_sample)

print(f'\n新样本预测类别：{target_names[predicted_class][0]}')

运行结果：

代码解析

数据加载：使用load_iris获取内置数据集，包含 4 个特征和 3 个类别标签，适合入门练习。

数据划分：将数据分为训练集（用于模型学习）和测试集（用于评估性能），确保模型能泛化到新数据。

K 值优化：通过交叉验证测试不同 K 值的性能，并用可视化方式直观展示 K 值对准确率的影响，最终选择最优 K 值。

模型评估：除准确率外，classification_report提供精确率、召回率等指标，全面评估模型在每个类别的表现。

新样本预测：演示如何用训练好的模型对未知样本进行分类，输出具体的类别名称。