支持向量机 Support Vector Machine （SVM）初步理解

文章目的：对支持向量机的内容有一个初步的了解。为了弄懂其中的内容查阅了很多资料，所以里面应该会有引用其他帖子的部分内容，如果原作者看到可以私信我，我会将您的帖子的地址付到下面。

简介

支持向量机（support vector machines）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。

SVM可分为三种模型：线性可分支持向量机与硬间隔最大化（hard margin maximization），线性支持向量机与软间隔最大化（soft margin maximization）和非线性支持向量机与核函数。即：

1. 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
2. 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
3. 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；

二、线性可分支持向量机与硬间隔最大化

          线性可分，就是指至少存在一个超平面，能把正例跟负例完全分隔开，那么这个数据集就是线性可分的。

1、间隔最大化和支持向量

如果一个线性函数能够将样本分开，称这些数据样本是线性可分的。那么什么是线性函数呢？其实很简单，在二维空间中就是一条直线，在三维空间中就是一个平面，以此类推，如果不考虑空间维数，这样的线性函数统称为超平面。我们看一个简单的二维空间的例子，O代表正类，X代表负类，样本是线性可分的，但是很显然不只有这一条直线可以将样本分开，而是有无数条，我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。

要求间隔最大的原因：一般来说，一个点距离超平面的远近可以表示分类预测的确信度，如图中的A，B两个样本点，B点被预测为正类的确信度要大于A点，所以SVM的目标是寻找一个超平面，使得离超平面较近的异类点之间能有更大的间隔，即不必考虑所有样本点，只需让求得的超平面使得离它近的点间隔最大。

硬间隔最大化：由于硬间隔是存在于数据集线性可分的情况下，且能把所有的样本点正确分在超平面两侧。因此线性可分支持向量机的间隔最大化就是指硬间隔最大化。

支持向量：离超平面越近的越难分是正例还是负例，要想加新的点以后预测更准确，就要使得 样本点到超平面的最小距离l最大  （距离越大越容易分类）而这个能得到最小距离L的样本点（距离超平面最近的点）就叫做支持向量。支持向量一定是正负例都有的，它是平行于超平面，到超平面的距离为L的两个超平面上的样本点。

如何进行间隔最大化？如何计算间隔？

怎么计算间隔？只有计算出了间隔，才能使得间隔最大化。在样本空间中，划分超平面可通过如下线性方程来描述： 
 
其中w为法向量，决定了超平面的方向，b为位移量，决定了超平面与原点的距离。假设超平面能将训练样本正确地分类，即对于训练样本(xi,yi)，满足以下公式： 
 
公式（2）称为最大间隔假设，yi=+1表示样本为正样本，yi=−1表示样本为负样本，式子前面选择大于等于+1，小于等于-1只是为了计算方便，原则上可以是任意常数，但无论是多少，都可以通过对 w 的变换使其为 +1 和 -1 ，此时将公式（2）左右都乘以 yiyi，得到如下：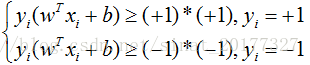 
 
实际上等价于： 
 
训练集中的所有样本都应满足公式（3）。如下图所示，距离超平面最近的这几个样本点满足 yi(wTxi+b)=1yi(wTxi+b)=1，它们被称为“支持向量”。虚线称为边界，两条虚线间的距离称为间隔（margin）。 

下面我们开始计算间隔，其实间隔就等于两个异类支持向量的差在 w 上的投影，即： 
 
其中 和