博弈学习博客

学习博客

巴什博奕

巴什博奕（Bash Game）：只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

首先我们来玩一个比较古老的报数游戏。A和B一起报数，每个人每次最少报一个,最多报4个。轮流报数,看谁先报到30.
如果不知道巴什博弈的可能会觉得这个是个有运气成分的问题，但是如果知道的人一定知道怎样一定可以赢。

我们先看下一个一眼就能看出答案的例子 比如说我们报到5(4+1),每次报最多报4个,最少报1个.那么是不是后者一定可以赢呢？答案是肯定的。好了到这巴什博弈的精髓基本就OK了。
那么如果我们要报到 $n+1$ ,每次最多报 $n$ 个,最少报 $1$ 个的话,后者一定能够赢。
现在我们需要报数到 $n$,而每次最多报数 $m$ 个,最少报数 $1$ 个.我们可以化成这样
$n=k\ast (1+m)+r(0<=r<=m）$这样的话如果 $r$ 不等于 $0$ 那么先手一定会赢，为什么呢？首先先手报 $r$ 个,那么剩下 $k$ 倍 $(1+m)$ 个数，如果后手报 $x$ 个，那么我们每次报数 $1+m-x$ 个数，就一定能保证最后剩下 $1+m$ 的倍数个，始终让后手面临 $(m+1)$ 的倍数的局面，先手就一定会赢，如果 $r=0$ 那么后手一定会赢，道理一样的。
即 $n\%(m+1)\ne 0$，( $r$ 为任意自然数, $s\le m$), 则先取者肯定获胜

在最后取光者获胜的规则中
谁先面临 $n\%(m+1)\ne 0$ 的局势，谁就输

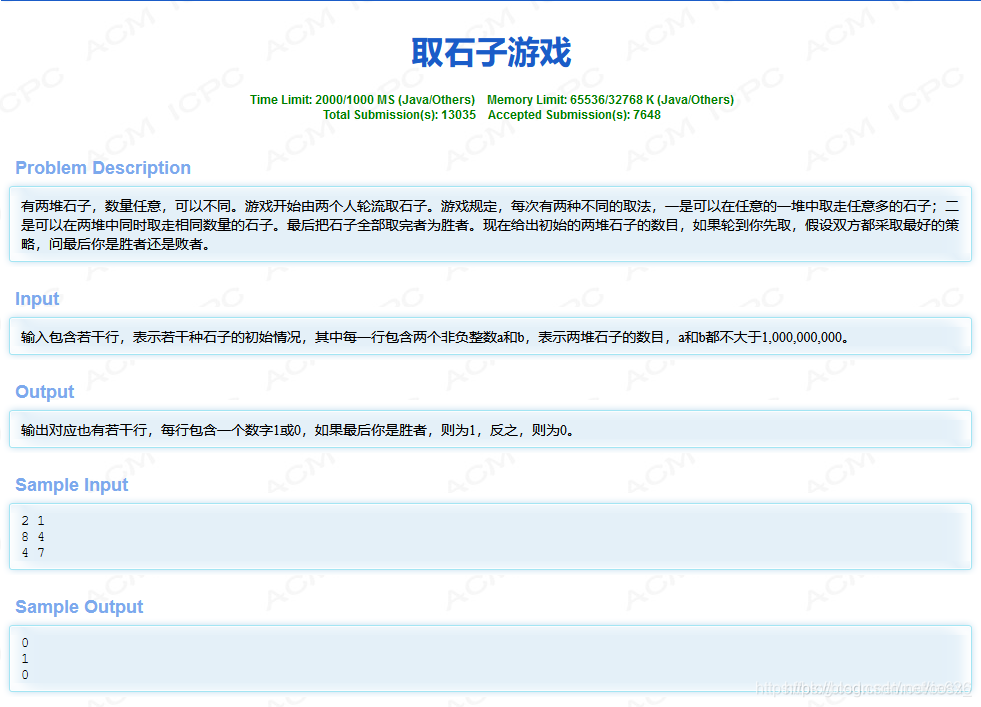
威佐夫博弈

威佐夫博弈：有两堆各若干个物品，两个人轮流从某一堆或同 时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

其中涉及一些数学的推导，不会证明。
结论：（0，0），（1，2），（3，5），（4，7）……（a，b）这些状态为必败局面，
规律是（b-a）*1.618=a则为必败局面（假设a为a，b中的较小值）。
1）给你一个局面，让你求是先手输赢。
有了上面的分析，那么这个问题应该不难解决。首先求出差值，差值 * 1.618 == 最小值 的话后手赢，否则先手赢。（注意这里的1.618最好是用上面式子计算出来的，否则精度要求高的题目会错）

2）给你一个局面，让你求先手输赢，假设先手赢的话输出他第一次的取法。
首先讨论在两边同时取的情况，很明显两边同时取的话，不论怎样取他的差值是不会变的，那么我们可以根据差值计算出其中的小的值，然后加上差值就是大的一个值，当然能取的条件是求出的最小的值不能大于其中小的一堆的石子数目。
假如在一堆中取的话，可以取任意一堆，那么其差值也是不定的，但是我们可以枚举差值，差值范围是0 — 大的石子数目，然后根据上面的理论判断满足条件的话就是一种合理的取法。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
int main()
{
    int n, m, a,b;
    while (cin >> n >> m)
    {
        a = max(n, m);
        b = min(n, m);
        double f = (sqrt(5) + 1) / 2.0;
        if (b == int((a-b) * f))cout << 0 << endl;
        else cout << 1 << endl;
    }
}

尼姆博奕

尼姆博奕（Nimm Game）：有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

尼姆博弈模型可以推广到：有n堆若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。
这个游戏中的变量是堆数k和各堆的物品数N1，N2，……，Nk。
对应的组合问题是，确定先手获胜还是后手获胜以及两个游戏人应该如何取物品才能保证自己获胜。

hdu 1850（第三次训练赛有写题解）

桌子上有M堆扑克牌；每堆牌的数量分别为Ni(i=1…M)；两人轮流进行；每走一步可以任意选择一堆并取走其中的任意张牌；桌子上的扑克全部取光，则游戏结束；最后一次取牌的人为胜者。
现在我们不想研究到底先手为胜还是为负，我只想问大家：
——“先手的人如果想赢，第一步有几种选择呢？”

Input
输入数据包含多个测试用例，每个测试用例占2行，首先一行包含一个整数M(1<M<=100)，表示扑克牌的堆数，紧接着一行包含M个整数Ni(1<=Ni<=1000000，i=1…M)，分别表示M堆扑克的数量。M为0则表示输入数据的结束。

Output
如果先手的人能赢，请输出他第一步可行的方案数，否则请输出0，每个实例的输出占一行。

Sample Input
3
5 7 9
0

Sample Output
1

经典的博弈题啊，必须弄懂必败点条件。这里是对n堆的牌数去异或，如果值为0则表示必败。题目问我们第一布有哪几种方法胜利。
即就是第一步能够给对手构建多少个必败点。
由于一次只能对一堆排进行操作，假设我 操作第i堆牌（a张），抽出x张。
那么其余n-1堆牌的异或值是固定为b.
那么 （a - x）^ b == 0 时，对手必败。
到此可能有人像我一样觉得必须历遍所有a求出那个值x满足条件。其实不必要
由上式可知x只有唯一取值
而且 一个数 与 b 异或等于 0 即表明 这个数等于b.
所以反过来我们可以求出b, 令 a - x = b ;
则 x = a - b，因为 x > 0，所以 a - b > 0
即只要b满足 b < a; 即能构造出x使得 （a - x）^ b == 0 时，对手必败！

# include<stdio.h>
int main()
{
    int n,i,sum,cnt;
    int p[105];
    while(scanf("%d",&n)&&n)
    {
        cnt=0;
        sum=0;
        for(i=0;i<n;i++)
        {
            scanf("%d",&p[i]);
            sum^= p[i];
        }
        for(i=0;i<n;i++)
        {
            if(p[i]>(sum^p[i]))//注意'^'的优先级小于'>'
            // sum^p[i]，这样求的是除p[i]以外所有数的异或
                cnt++;
        }
        printf("%d\n",cnt);
    }
    return 0;
}

GCD Game-hdu-7061
题意：给你 $n$ 个数，每次操作 选取一个 $a_i(1<=a_i<=1e7)$，然后选取一个 $x(1<=x<a_i)$，用 $gcd(a_i,x)$代替 $a_i$，谁最后无法操作将输掉比赛，对应尼姆博弈种最后取光者胜利和至少每次操作取一次石子，$Alice$ 先手。
分析：当 $a_i$ 变成 $1$ 就无法操作了，相当于第 $i$ 堆石子取光了，$a_i$所有质因子的个数就相当于石子数。
我们只需要统计每个 $a_i$ 的质因子个数即可
由于$a_i$比较大，每次单独求质因子个数显然会T，考虑线性筛统计因子，每次将 $i\ast p[j]$ 这个合数标记操作 $v[i\ast p[j]]=1$ ，我们可以写成 $v[i\ast p[j]]=v[i]+1（i多了p[j]这个质因子）$，即将合数标记了，而且还统计了这个合数的质因子个数，注意由于 $v[i]$初始化的是 $0$ 而不是 $1$，因此实际是比质因子数少 $1$ 的。
预处理完每个数的质因子个数就变成了经典的尼姆博弈问题

反尼姆博弈

有任意堆物品，每堆物品的个数是任意的，双方轮流从中取物品，每一次只能从一堆物品中取部分或全部物品，最少取一件，取到最后一件物品的人失败。

下面直接给出反尼姆博弈中判断必胜局的条件，满足其中任意一点都能取胜：
1.各堆物品数目异或结果不等于0，且存在有石子数目大于1的物品堆
2.各堆物品数目异或结果等于0，且所有物品堆数目全部为1
分析博客

楼教主的男人八题
奇妙的取石子
取石子（三）
思路：
当只有一堆石子的时候那是必胜态
两堆石子的时候：如果两堆石子数量一样就是必败态，因为后手可以跟着前手一样在另一堆石子上面操作，最后一个拿石子的肯定是后手
如果两堆石子数量不一样那就是必胜态，因为前手可以通过一次操作使两堆石子数量不一样变成一样，就转化成了上面那一种情况
三堆石子的时候也是必胜态，因为前手可以一次操作使它变成两堆石子的第一种情况：
例如：三堆石子数量是 $x<y<z$
我们可以先用 $z$ 把 $x$ 补齐到 $y$，然后再把 $z$ 剩下的石子拿走
如果三堆中有两堆直接相同，那就直接拿走不相同的那一堆就可以了
四堆石子的时候：如果他们两两相同或者都一样的情况下，那么就符合两堆石子的第一种状态，必败态。如果他们都不相同，例如： $x<y<z<w$，这个时候可以用 $w$ 将 $y$ 补齐到 $z$ ，之后再让 $w$ 的石子剩下 $x$ 个就可以了（可能有人会怀疑 $w$ 可能在某种情况下补齐完 $y$ ，就刚好等于 $x$ ，不能再拿石子了。这种情况是不存在的，因为我们这样操作相当与在问你 $y+w>x+z$ 吗，显然这是成立的，那么你的怀疑也就不攻自破了）
可以得到如果是奇数堆，就可以构造必败态给后手，先手必胜
否则如果当前状态由若干必败态（石子数相同的两两成对）构成，那么就必败，判断一下即可
code：

#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m;
int cnt[109];

void work()
{
	mem(cnt, 0);
	for(int i = 1, x; i <= n; ++i){
		cin >> x;cnt[x]++;
	}
	if(n & 1) cout << "Win" << endl;
	else {
		for(int i = 1; i <= 100; ++i) if(cnt[i] & 1){
			cout << "Win" << endl;
			return;
		}
		cout << "Lose" << endl;
	}
}

int main()
{
	ios::sync_with_stdio(0);
//	int TT;cin>>TT;while(TT--)
	while(cin >> n && n)
	work();
	return 0;
}