【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
西瓜书《机器学习》+南瓜书《机器学习公式讲解》。
task01 概览西瓜书+南瓜书1、2
第1章:https://www.bilibili.com/video/BV1Mh411e7VU?p=2
第2章:第2章严格来说是在学完具体机器学习算法后再来学的,因此本章能看懂多少就看多少,只需看到2.3.2即可,【2.3.3-ROC与AUC】及其以后的暂时都可以跳过,等学完后面的算法再回来认真研读。
课程:西瓜书算法的公式推导,原理概述(自行预习西瓜书)。先看西瓜书熟悉概念,看课学习算法原理和公式推导,回西瓜书看其他。
- 高等数学:求偏导
- 线性代数:矩阵运算
- 概率论与数理统计:随机变量,简单的数学分布
第一章 绪论
机器学习的定义:让计算机来学习“经验”数据,生成一个算法模型,面对新的情况,计算机便能作出有效的判断。
形式化的定义(Mitchell),假设:
P:计算机程序在某任务类T上的性能。
T:计算机程序希望实现的任务类。
E:表示经验,即历史的数据集。
若该计算机程序通过利用经验E在任务T上获得了性能P的改善,则称该程序对E进行了学习。
把学习过程看作一个在所有假设组成的空间(假设空间)中进行搜索的过程,目标是找到与训练集“匹配”的假设。可能有多个假设与训练集一致,即存在着一个与训练集一致的“假设集合”,称为版本空间。
归纳偏好
(多个假设都匹配,如何选定一个):机器学习算法在学习过程中对某种类型假设的偏好,称为“归纳偏好”,任何一个有效的机器学习算法必有其偏好。通用的原则是“奥卡姆剃刀”,选择最简单的那个,而在实际问题中,算法的归纳偏好是否与问题本身匹配,大多是时候直接决定了算法能否取得好的性能。
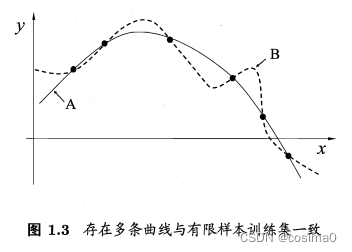
“没有免费的午餐”(NFL)定理:一个算法A若在某些问题上比另一个算法B好,必存在另一些问题,在那里B比A好。——总误差与算法无关,不同算法的期望性能相同(前提:所有“问题”出现机会相同,或所有问题同等重要)。[证明]
——选择算法时,算法的归纳偏好应与具体问题匹配。
第二章 模型评估与选择
经验误差与过拟合
训练误差/经验误差:学习器在训练集上的误差
泛化误差:测试集(新样本)上的误差
希望得到泛化误差小的学习器,让学习器尽可能地从训练集中学出普适性的“一般特征”,这样在遇到新样本时才能做出正确的判别。然而,当学习器把训练集学得“太好”的时候,即把一些训练样本的自身特点当做了普遍特征;同时也有学习能力不足的情况,即训练集的基本特征都没有学习出来。
学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了(过拟合)。学习能太差,训练样本的一般性质尚未学好(欠拟合)。
在过拟合问题中,训练误差十分小,但测试误差教大;在欠拟合问题中,训练误差和测试误差都比较大。目前,欠拟合问题比较容易克服,例如增加迭代次数等,但过拟合问题还没有十分好的解决方案,过拟合是机器学习面临的关键障碍。
评估方法
我们无法直接获得泛化误差,通常采用一个“测试集”来测试学习器对新样本的判别能力,然后以“测试集”上的“测试误差”作为“泛化误差”的近似。测试集应与训练集互斥。
1.留出法:将数据集D划分为两个互斥的集合,一个作为训练集S,一个作为测试集T,满足D=S∪T且S∩T=∅。分层抽样,若干次随机划分取均值。
2.交叉验证法:将数据集D划分为k个大小相同的互斥子集,满足D=D1∪D2∪…∪Dk,Di∩Dj=∅(i≠j),同样地尽可能保持数据分布的一致性,即分层抽样。每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,进行k次训练和测试,最终返回k个测试结果的均值。
“留一法”是交叉验证法的特例,此时k等于样本数m。(评估结果比较准确,消耗巨大)
3.自助法:基于自助采样。给定包含m个样本的数据集D,每次随机从D 中挑选一个样本,将其拷贝放入D’,然后再将该样本放回初始数据集D 中,使得该样本在下次采样时仍有可能被采到。重复执行m 次,就可以得到了包含m个样本的数据集D’。
参数选择
学习算法有些参数需要设定,参数配置不同,学得模型的性能往往有显著差别,这就是参数调节/调参。
常用的做法是:对每个参数选定一个范围和步长λ,这样使得学习的过程变得可行。例如:假定算法有3 个参数,每个参数仅考虑5 个候选值,这样对每一组训练/测试集就有555= 125 个模型需考察。
当选定好模型和调参完成后,我们需要使用初始的数据集D重新训练模型,即让最初划分出来用于评估的测试集也被模型学习,增强模型的学习效果。
算法的参数一般由人工设定,亦称“超参数”,模型的参数一般由学习确定。
性能度量
性能度量是衡量模型泛化能力的评价标准,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评判结果。
均方误差MSE

错误率与精度
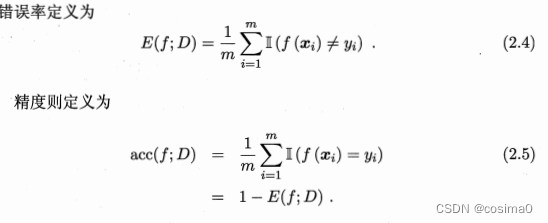
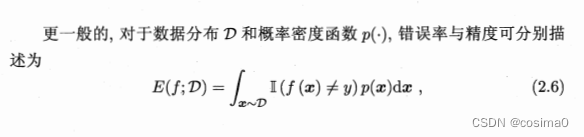
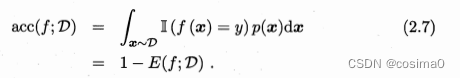
查准率、查全率与F1





















 381
381

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








