【机器学习四】主成分分析降维算法-PCA

本文链接：https://blog.youkuaiyun.com/cooper_1/article/details/105200434

本文深入讲解主成分分析(PCA)算法，探讨其在数据降维、噪音消除和压缩中的应用。解析PCA原理，包括最小投影距离和最大投影方差推导，提供算法流程和Python实现代码，分析优缺点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

主成分分析PCA算法

主成分分析(Principal components analysis)，简称PCA，是最重要的数据降维算法之一。广泛的用于数据噪音消除和数据压缩消除冗余等领域。

一、降维

常见的数据降维方法有：奇异值分解(SVD)、主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)。

降维的必要性：

多重共线性和预测变量之间相互关联。多重共线性会导致解空间的不稳定，从而可能导致结果的不连贯。
高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有2%。
过多的变量，对查找规律造成冗余麻烦。
仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。

降维的目的：

减少预测变量的个数。
确保这些变量是相互独立的。
提供一个框架来解释结果。相关特征，特别是重要特征更能在数据中明确的显示出来；如果只有两维或者三维的话，更便于可视化展示。
数据在低维下更容易处理、更容易使用。
去除数据噪声。
降低算法运算开销。

二、PCA的原理及推导

2.1 PCA思想

PCA可解决训练数据中存在数据特征过多或特征累赘的问题。核心思想是将m维特征映射到n维（n < m），这n维形成主元，是重构出来最能代表原始数据的正交特征。

假设数据集是m个n维， $,x(m))(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, \cdots, \boldsymbol x^{(m)})$ 。如果 $n = 2$ ，需要降维到 $n^{'} = 1$ ，现在想找到某一维度方向代表这两个维度的数据。下图有 $u_1, u_2$ 两个向量方向，但是哪个向量才是我们所想要的，可以更好代表原始数据集的呢？
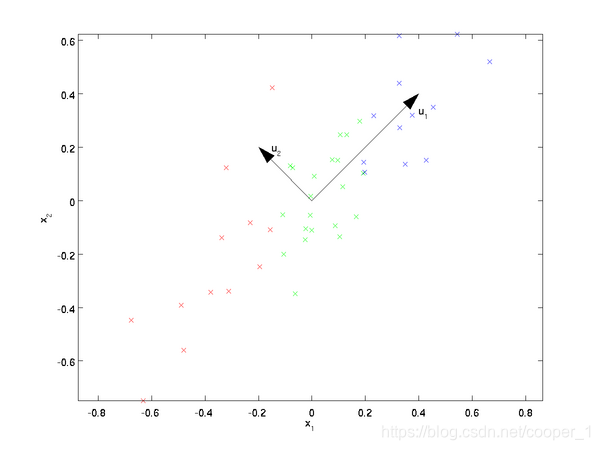
在这里插入图片描述
从图可看出， $u_1$ 比 $u_2$ 好，为什么呢？有以下两个主要评价指标：

样本点到这个直线的距离足够近。
样本点在这个直线上的投影能尽可能的分开。

如果我们需要降维的目标维数是其他任意维，则：

样本点到这个超平面的距离足够近。
样本点在这个超平面上的投影能尽可能的分开。

那么基于这两个标准，我们可以得到PCA推导的两种方法：基于最小投影距离和基于最大投影方差

2.2 基于最小投影距离的PCA推导

基于最小投影距离方法的评价标准是样本点到超平面的距离最小

假设数据集是m个n维， $x^{(1)}, x^{(2)},...,x^{(m)})$ ，且数据进行了中心化（零均值化，即 $∑i=1mxi=0\sum\limits^{m}_{i=1}x^{i}=0$ ）。经过投影变换得到新坐标为 ${w_1,w_2,...,w_n}$ ，其中 $w$ 是标准正交基，即 $w \|_2 = 1$ ， $wiTwj=0w^T_iw_j = 0$ 。

经过降维后，新坐标为 ${ w_1,w_2,...,w_n \}$ ，其中 $n^{'}$ 是降维后的目标维数。样本点 $x^{(i)}$ 在新坐标系下的投影为 $z(i)=(z1(i),z2(i),...,zn′(i))z^{(i)} = \left(z^{(i)}_1, z^{(i)}_2, ..., z^{(i)}_{n'} \right)$ ，其中 $zj(i)=wjTx(i)z^{(i)}_j = w^T_j x^{(i)}$ 是 $x^{(i)}$ 在低维坐标系里第 j 维的坐标。

如果用 $z^{(i)}$ 去恢复 $x^{(i)}$ ，则得到的恢复数据为 $x^(i)=∑j=1n′xj(i)wj=Wz(i)\widehat{x}^{(i)} = \sum^{n'}_{j=1} x^{(i)}_j w_j = Wz^{(i)}$ ，其中 $W$ 为标准正交基组成的矩阵。

考虑到整个样本集，样本点到这个超平面的距离足够近，目标变为最小化 $∑i=1m∥x^(i)−x(i)∥22\sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2$ 。对此式进行推理，可得：
$∑i=1m∥x^(i)−x(i)∥22=∑i=1m∥Wz(i)−x(i)∥22=∑i=1m(Wz(i))T(Wz(i))−2∑i=1m(Wz(i))Tx(i)+∑i=1m(x(i))Tx(i)=∑i=1m(z(i))T(z(i))−2∑i=1m(z(i))Tx(i)+∑i=1m(x(i))Tx(i)=−∑i=1m(z(i))T(z(i))+∑i=1m(x(i))Tx(i)=−tr(WT(∑i=1mx(i)(x(i))T)W)+∑i=1m(x(i))Tx(i)=−tr(WTXXTW)+∑i=1m(x(i))Tx(i) \sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2 = \sum^m_{i=1} \| Wz^{(i)} - x^{(i)} \|^2_2 \\ = \sum^m_{i=1} \left( Wz^{(i)} \right)^T \left( Wz^{(i)} \right) - 2\sum^m_{i=1} \left( Wz^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) - 2\sum^m_{i=1} \left( z^{(i)} \right)^T x^{(i)} + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = - \sum^m_{i=1} \left( z^{(i)} \right)^T \left( z^{(i)} \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^T \left( \sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T \right)W \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)} \\ = -tr \left( W^TXX^TW \right) + \sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)}$
在推导过程中，分别用到了 $x‾(i)=Wz(i)\overline{x}^{(i)} = Wz^{(i)}$ ，矩阵转置公式 $AB)^T = B^TA^T$ ， $W^TW = I$ ， $z^{(i)} = W^Tx^{(i)}$ 以及矩阵的迹，最后两步是将代数和转为矩阵形式。
由于 $W$ 的每一个向量 $w_j$ 是标准正交基， $∑i=1mx(i)(x(i))T\sum^m_{i=1} x^{(i)} \left( x^{(i)} \right)^T$ 是数据集的协方差矩阵， $∑i=1m(x(i))Tx(i)\sum^m_{i=1} \left( x^{(i)} \right)^T x^{(i)}$ 是一个常量。最小化 $∑i=1m∥x^(i)−x(i)∥22\sum^m_{i=1} \| \hat{x}^{(i)} - x^{(i)} \|^2_2$ 又可等价于
$\underbrace{\arg \min}_W - tr \left( W^TXX^TW \right) s.t.W^TW = I$
利用拉格朗日函数可得到
$-tr(W^TXX^TW) + \lambda(W^TW - I)$
对 $W$ 求导，可得 $−XXTW+λW=0-XX^TW + \lambda W = 0$ ，也即 $XXTW=λWXX^TW = \lambda W$ 。 $XX^T$ 是 $n^{'}$ 个特征向量组成的矩阵， $λ\lambda$ 为 $XX^T$ 的特征值。 $W$ 即为我们想要的矩阵。
对于原始数据，只需要 $z^{(i)} = W^TX^{(i)}$ ，就可把原始数据集降维到最小投影距离的 $n^{'}$ 维数据集。

2.3 基于最大投影方差的PCA推导

对于任意一个样本 $x (i)$ ，在新的坐标系中的投影为 $W^Tx^{(i)}$ ,在新坐标系中的投影方差为 $x^{(i)T}WW^Tx^{(i)}$ ，要使所有的样本的投影方差和最大，也就是最大化 $∑i=1mWTx(i)x(i)TW\sum\limits^{m}_{i=1}W^Tx^{(i)}x^{(i)T}W$ 的迹,即：
$\underbrace{\arg\max}_{w} tr \left( W^TXX^TW \right) s.t.W^TW = I$
对比最小投影距离的优化方程，可以发现都是一样的，一个是负号的最小化，一个是正的最大化，所以计算过程是一样的，不再计算。

三、PCA算法流程

输入： $n$ 维样本集 $\left( x^{(1)},x^{(2)},...,x^{(m)} \right)$ ，目标降维的维数 $n^{'}$ 。

输出：降维后的新样本集 $\left( z^{(1)},z^{(2)},...,z^{(m)} \right)$ 。

主要步骤如下：

对所有的样本进行中心化， $x(i)=x(i)−1m∑j=1mx(j)x^{(i)} = x^{(i)} - \frac{1}{m} \sum^m_{j=1} x^{(j)}$ 。
计算样本的协方差矩阵 $XX^T$ 。
对协方差矩阵 $XX^T$ 进行特征值分解。
取出最大的 $n’ $ 个特征值对应的特征向量 ${ w_1,w_2,...,w_{n'} \}$ 。
标准化特征向量，得到特征向量矩阵 $W$ 。
转化样本集中的每个样本 $z^{(i)} = W^T x^{(i)}$ 。
得到输出矩阵 $\left( z^{(1)},z^{(2)},...,z^{(n)} \right)$ 。
注：在降维时，有时不明确目标维数，而是指定降维到的主成分比重阈值 $\epsilon(0,1])$ 。假设 $n$ 个特征值为 $λ1⩾λ2⩾...⩾λn\lambda_1 \geqslant \lambda_2 \geqslant ... \geqslant \lambda_n$ ，则 $n^{'}$ 可从 $∑i=1n′λi⩾k×∑i=1nλi\sum^{n'}_{i=1} \lambda_i \geqslant k \times \sum^n_{i=1} \lambda_i$ 得到。

四、手撕PCA代码

'''
手写PCA降维算法
'''

import numpy as np

def PCA(X,n):
    X_mean = np.mean(X,axis=1)
    X = X - X_mean.reshape(-1,1)
    # 求协方差矩阵
    cov_mat = np.dot(X,X.T)
    # 将协方差进行特征值分解 第一个返回值是特征值矩阵，第二个返回值是特征向量矩阵
    values,vectors = np.linalg.eig(cov_mat)
    # 按特征值将特征向量进行排序
    # 拼接一个特征值和特征向量一起的矩阵
    eig_mat = [(np.abs(values[i]),vectors[:,i]) for i in range(len(X))]
    # 排序
    eig_mat.sort(reverse=True)
    # 拼接WT矩阵 降维后的权重矩阵，只保留要保留的列
    WT = np.array([_[1] for _ in eig_mat[:n]])
    # 对X进行转换，降维
    return np.dot(WT,X)

# 数据生成 直接转置，因为协方差矩阵A = (X - X.mean).T
#(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)
X = np.transpose(np.array([[2.5,2.4], [0.5,0.7], [2.2,2.9], [1.9,2.2], [3.1,3.0], [2.3, 2.7],[2, 1.6],[1, 1.1],[1.5, 1.6],[1.1, 0.9]]))
# 降至的维度
n = 1

if __name__ == "__main__":
    X = PCA(X,n)
    print(X)

五、PCA算法主要优缺点

优缺点	简要说明
优点	1. 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　2.各主成分之间正交，可消除原始数据成分间的相互影响的因素。3. 计算方法简单，主要运算是特征值分解，易于实现。
缺点	1.主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。