背包问题详解_背包问题的程序解析有哪些-优快云博客

本文链接：https://blog.youkuaiyun.com/cook_for_you/article/details/123563153

01背包问题以及优化

其实在写题解的时候不是在告诉别人，而是在教会自己！

作者的话

本篇题解面向想学算法的小白，或者对背包问题百思不得其解的小伙伴
作者尽量采用了不同的视角，不同的方式去描述和解决问题
- 题解模板
- 图解算法
- 手工模拟
希望大家喜欢！
由于作者水平有限，如果有路过的小伙伴或者大神看出本篇题解的问题或者不足，还请评论！
本人感激不尽！

01背包问题的赘述

用一句话描述背包问题

背包问题就是在有限集里面的最优解问题

有限的物品（每个物品仅有一个）
有限的空间（限制条件）
求最大值

01背包问题的代码（未优化）

#include <bits/stdc++.h>
using namespace std;
int n, m;				//n代表物品个数，m代表背包空间
const int N = 1010;
int f[N][N];			//f[i][j]里面存放的数据为，空间为 j 时，有 i 个物品可选择时的，最大值
int v[N], w[N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) {
		cin >> v[i] >> w[i];
	}
	f[0][0] = 0;		//状态初始化，但是因为f[][]是全局变量，所有自动初始化，所有本行可加可不加
	//精华内容见文章分析
	//start
	for (int i = 1; i <= n; ++i) {
		for (int j = 0; j <= m; ++j) {
			f[i][j] = f[i - 1][j];
			if (j >= v[i]) {
				f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
			}
		}
	}
	//end
	cout << f[n][m];
	return 0;
}

01背包问题的精华代码解析

抛开代码和动态规划，如果让我们来做选择，我们会怎么做？

先挑最贵的拿
然后再去尽可能的去塞满空间

但是，我们说上面的那种拿法很可能不是最优解

贪心并不能保证最优解，只有理智的思考才能到达彼岸

所有我们选择借助表格来帮助判断

首先，规定一下横向和纵向分别代表什么意思

然后，你一步步的填完整张表格

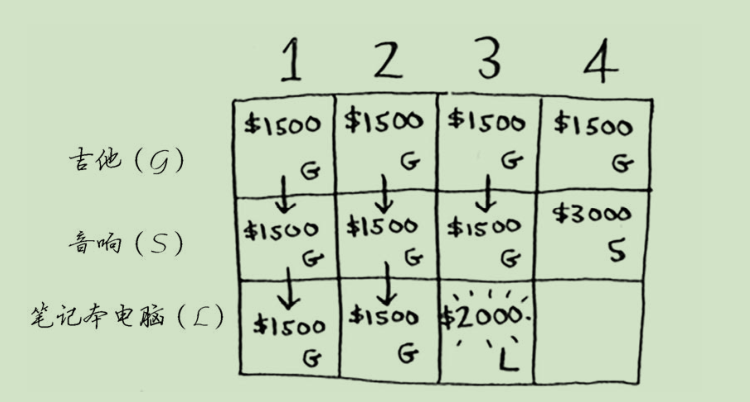
最后，你果断选择了拿音响和吉他，却放弃了笔记本

其实，你可知道，你已经做了一次动态规划

动态规划就是把所有可能的组合不重不漏的列出来，然后循环取其中的最大值。

铺垫了这么多，不知道你是否理解这短短五行代码的含义了

for (int i = 1; i <= n; ++i) {
		for (int j = 0; j <= m; ++j) {
			f[i][j] = f[i-1][j ];
			if (j >= v[i]) {
				f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
			}
		}
	}

为什么是从1开始？

代码是有实际意义的！

i 代表物品，如果没有物品，那么价值肯定是0，所有从 0 开始循环没有任何意义。
内循环，j 表示背包空间。
如果能保证 j > v[i] 也就是把内循环的判断条件改一下，那么就可以直接写
```
f[i][j] = max(f[i][j-1], f[i - 1][j - v[i]] + w[i]);
```
第二次判断条件，可以放到 for 循环里面去判断
状态转移方程
- 01是什么意思，0 代表不取整个物品， 1 代表取这个物品
- 动态规划是递推，尾递归或者递归是递归。（递推的下一个值是简历在前面值已知的基础上，而递归则是从顶部开始，一步步去逼近答案）
- 我们按照最后一个物品取还是不取（这里的最后一个物品并不是全部物品里面的最后一个物品，而是每次外循环所代表的物品总数的最后一个物品）

优化代码

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1010;
int f[N];
int v[N], w[N];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) {
		cin >> v[i] >> w[i];
	}
    //精华部分
    //start
	for (int i = 1; i <= n; ++i) {
		for (int j = m; j >= v[i]; --j) {
			f[j] = max(f[j], f[j - v[i]] + w[i]);
		}
	}
    //end
	cout << f[m];
	return 0;
}

优化的代码的精华部分解析

可能你还没看出啦优化了哪里

原本存放结果的二维数组被压缩成一维的了

即，由 f[N][N] ==> f[N]

可以注意到，与未优化的代码相比，背包的空间是由 从小到大循环 变成了 从大到小循环

下面就来解释一下从大到小循环的妙处

其核心问题就是

代码里面两个 f [ j ] 是否相同

正确答案是：不相同

下面，请听我，细细道来。

先说运算符的优先级问题， “=” 的优先级仅比 “,” 高。所有，先算右边的比较，再进行赋值。
那么，第二个 f [ j ] 代表的是什么？很明显代表上一轮的 j 容量下最大的价值，也就是 f [ i-1 ][ j ]
所有第一个是更新后的 j 内存下的最大值

为什么要逆序循环

结论：因为正序循环，第二个f [ i ] 代表这一轮的也就是 **f [ i ] [ j ] **

给想真正学懂的小伙伴一个建议，那就是自己去亲自用纸演算一遍

实在不想动手的可以看我下面的演算过程

假设：

物品数量为 3，背包空间为 4；

物品	空间	价值
1.吉他	1	1500
2.音响	4	3000
3.笔记本电脑	3	2000

逆序

 f(4) = max(f(4), f(3)+1500)      //此时 f(3) = 0 && f(4) = 0 ==> f(4) = 1500
 f(3) = max(f(3), f(2)+1500)      //下面的原因类似，不再赘述
 f(2) = max(f(2), f(1)+1500) 
 f(1) = max(f(1), f(0)+1500)
 ————————————————————————————————————————————————————————————————————————————————————————————————————
 f(4) = max(f(4), f(0)+3000)	  //此时， f(0) = 0 && f(4) = 1500 ==> f(4) = 3000
 f(3) = f(3)    				 //因为 j < v[i], 所有并没有更新下面这些值
 f(2) = f(2) 
 f(1) = f(1)
 ---------------------------------------------------------------------------------------------------
f(4) = max(f(4), f(1)+2000)		 //此时， f(1) = 1500 && f(4) = 3000 ==> f(4) = 3500
f(3) = max(f(3), f(0)+2000)      //此时， f(0) = 0 && f(3) = 1500 ==> f(4) = 2000
f(2) = f(2) 				    因为 j < v[i], 所有并没有更新下面这些值
f(1) = f(1)

~~好了，逆序我写完了，正序改你自己尝试一下了吧~~

想了一下，还是写上吧。

正序

f(1) = max(f(1), f(0) + 1500)		//f(0) = 0 && f(1) = 0 ==> f(1) = 1500
f(2) = max(f(2), f(1) + 1500)		//f(1) = 1500 && f(2) = 0 ==> f(2) = 3000
f(3) = max(f(3), f(2) + 1500)		//f(2) = 3000 && f(3) = 0 ==> f(3) = 4500
f(4) = max(f(4), f(3) + 1500)		//f(3) = 4500 && f(4) = 0 ==> f(4) = 6000
—————————————————————————————————————————————————————————————————————————————————————————————————————
f(1) = f(1)						   //以下三行， 因为 j < v[i] ,所有数据并没有更新
f(2) = f(2)
f(3) = f(3)
f(4) = max(f(4), f(1) + 3000)		//f(1) = 1500 && f(4) = 6000 ==> f(4) = 6000
-----------------------------------------------------------------------------------------------------
f(1) = f(1)						   //以下两行， 因为 j < v[i] ,所有数据并没有更新
f(2) = f(2)
f(3) = max(f(3), f(0)+2000)			//f(3) = 4500 && f(0) = 0 ==> f(3) = 4500
f(4) = max(f(4), f(1)+2000)			//f(4) = 6000 && f(1) = 1500 ==> f(4) = 6000