树等的学习

目录

目录

一、基本概念

二、二叉树的性质

三、树的操作

树的操作包括：

（一）树的初始化

（二）树的操作

三、总代码

---

---

一、基本概念

1、树的结构是双亲与孩子，也可以理解为一个节点有一个数据域和两个指针域（左右指针域）

2、二叉树树的遍历：前序、中序、后序、层序

3、已知二叉树的前序排列和中序排列，则可以确定树的形状

4、狭义上：每棵树都有一个根节点，根节点是唯一的

     广义上：每个树可以分为多个小树，所以广义的根节点也有多个

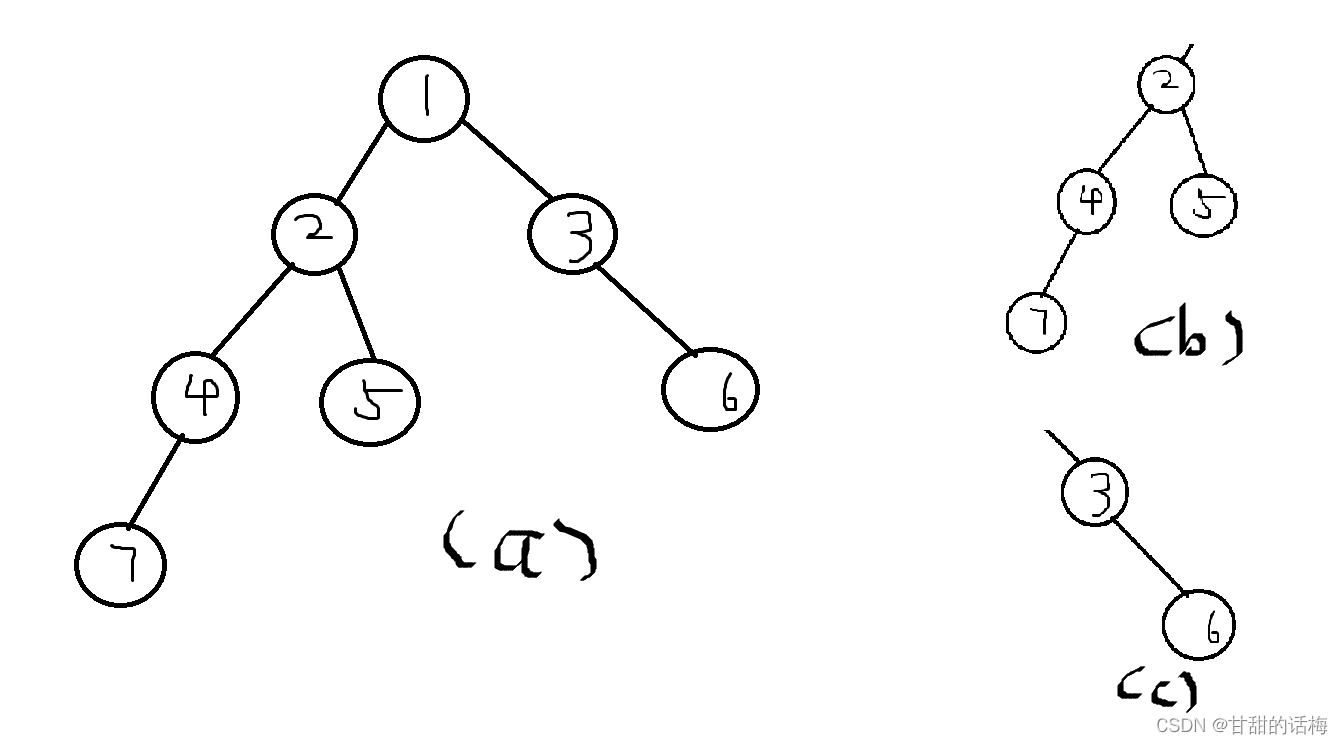
上图中，（a）中的根节点为序号1，此时的1即为狭义的根节点，也是广义的根节点，

（b）中的根节点是序号2，为狭义的根节点，因为（b）是（a）的小树，（c）同理；

二、二叉树的性质

性质1：在二叉树的第i层上至多有2^(i-1)个结点（i>=1）

性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）

性质3：任一个二叉树，如果其终端结点数为n0（度为0的结点），度为2的结点数为n2，度为1的结点数为n1，则满足n0=n2+1；

理解性质3：

（1）从点的角度来看，终端结点数为n0（度为0的结点），度为2的结点数为n2，度为1的结点数为n1，则n=n0+n1+n2（式子一）

（2）从结点头上的线来看，每个结点的头上都会有1条线，头上总线有n-1（因为根节点没有头上的线）；

而度为2的结点说明下面有2条线，度为1的结点说明下面有1条线，度为0的结点说明下面有0条线，则脚下总线有2*n2+1*n1+0*n0；

头上的总线应该=脚下的总线，故n-1=2*n2+1*n1+0*n0（式子二）；

（3）解式子一和式子二，可得n0=n2+1；

性质4：具有n个结点的完全二叉树的深度为(向下取整数)

性质5：

1. 结点i的左孩子是2i，右孩子是2i+1；（主）
2. 如果左孩子的标号为x，则双亲的标号为x/2；（推）
3. 若果右孩子的标号为y，则双亲的标号为（y-1）/2；（推）

三、树的操作

树的操作包括：

（一）树的初始化

1、树的节点结构

typedef struct treeNode
{
	int val;//数据域
	struct treeNode *lchild,*rchild;//左孩子右孩子，指针域
}BTNode;

2、树的维护结构

typedef struct
{
	int num;//计数
	BTNode *root;//根节点
}RTree;

    树的维护结构初始化

RTree* Init()
{
 	RTree *st=(RTree*)malloc(sizeof(RTree));
	st->num=0;
	st->root=NULL;
	return st;
}

（二）树的操作

1、新建树

void inserArrBTree(RTree *st,int *arr,int n)//插入树（树维护的地址，要插入的数组地址，要插入的数组元素的个数）
{
	int i=1;//数组的下标指针
	int head,rear;//定义队的头尾指针
	BTNode* queue[20]={0};//创建一个队列（用结构体指针数组实现，用来存放节点的指针）
	BTNode* cur;//出队的指针存储
	if(!st) return;
	if(st->root==NULL)//如果是第一个根节点则：
	{
		st->root=(BTNode*)malloc(sizeof(BTNode));//申请节点的内存空间赋给根节点
		st->root->lchild=st->root->rchild=NULL;//将节点的左右孩子都置为空
		st->root->val=arr[0];//将数组第一个数据存入根节点的数据域,往后的数据从i=1开始，到n-1结束
		st->num++;
	}

	//指针队列初始化
	head=-1;//头指针处没有数据的(参见队列的内容)
	rear=-1;//初始化队列，空队列head=rear
	queue[++rear]=st->root;//将根节点入队
		
	while(i<n)
	{
		cur=queue[++head];//队头（下标小的）出队
		
		if(cur->lchild)//左孩子如果不为空有节点
		{
			queue[++rear]=cur->lchild;//将这个节点入队
			st->num++;
		}
		else//左孩子如果为空没有节点
		{
			cur->lchild=(BTNode*)malloc(sizeof(BTNode));//申请新节点的内存和初始化
			cur->lchild->lchild=cur->lchild->rchild=NULL;
			cur->lchild->val=arr[i++];//将数组元素放入新的节点
			queue[++rear]=cur->lchild;
			st->num++;
		}

		if(i==n)break;//如果数组待处理的元素没有了，则返回

		if(cur->rchild)//右孩子如果不为空有节点
		{
			queue[++rear]=cur->rchild;//将这个节点入队
			st->num++;
		}
		else//右孩子如果为空没有节点
		{
			cur->rchild=(BTNode*)malloc(sizeof(BTNode));//申请新节点的内存和初始化
			cur->rchild->lchild=cur->rchild->rchild=NULL;
			cur->rchild->val=arr[i++];//将数组元素放入新的节点
			queue[++rear]=cur->rchild;
			st->num++;
		}
	}	
}

2、判断树空

int treenull(RTree* tp)
{
	return (!tp) ? 0 : ((!tp->num) ? 0 : 1); 
}

3、树的高度计算

int gaodufuzhu(BTNode* s)//树高度的计算辅助函数
{
	int left=0,right=0;//左右的高度
	if(!s)return 0;
	left=gaodufuzhu(s->lchild);
	right=gaodufuzhu(s->rchild);
	return (left>right) ? left+1 : right+1;//三目运算，left>right时返回left+1，否则left<right时返回right+1
}
int gaodu(RTree* tp)//树高度的计算调用函数
{
	if(!tp)return 0;
	return gaodufuzhu(tp->root);
}

4、清空树

int clearfuzhu(BTNode* tp,int *n)//-1(空)，n为 计数变量的地址
{
	int left,right;
	if(!tp) 
		return -1;
	left=clearfuzhu(tp->lchild,n);//递归算法
	right=clearfuzhu(tp->rchild,n);
	if((left==right)==-1);
	{
		free(tp);
		(*n)--;//*指针取值符，取出计数单位进行减操作
		return -1;
	}
	return 0;
}
int cleartree(RTree* st)//清空树的调用
{
	if(!st || !(st->num)) return 0;
	return clearfuzhu(st->root,&(st->num));//st->root是根节点的地址，&(st->num)是计数变量的地址
}

5、查找树的数据是否存在

BTNode* fuzhufind(BTNode* tp,int n)//返回的是一个节点的地址，n代表要查找的数据
{
	BTNode *left,*right;//定义左树根的地址（广义的根）和右树的根的地址（广义的根）
	if(!tp)return NULL;//判断广义节点是否为空
	if(tp->val==n)//广义节点部位空，查验此时的广义根的数据是否等于我们要找的数据
		return tp;//如果等于则返回这个广义节点的地址
	left=fuzhufind(tp->lchild,n);//若不等于则继续对这个广义节点的左孩子递归
	right=fuzhufind(tp->rchild,n);//左孩子结束后对右孩子递归
	return left ? left : (right ? right : NULL);//三目运算符，a？b:c--如果a为真则b执行，否则c执行
												//如果是在树的左边找到的，则返回左值，否则返回右值，没有找到返回NULL
}
BTNode* findtree(RTree* st,int n)//查找调用（根节点的地址，查找的数值），返回的是一个节点的地址
{
	if(!st) return NULL;//如果根节点为空，则返回空
	return fuzhufind(st->root,n);//调用查找的辅助函数并返回节点的地址
}

6、遍历（前中后层）

//前序遍历
void Qprinttree(BTNode* tp)//前序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	printf("%d ",tp->val);//输出根数据
	Qprinttree(tp->lchild);//看根的左孩子，如果左孩子存在，则输出，否则左孩子为空，则返回上一级
	Qprinttree(tp->rchild);//返回上一级后再看右，同样的，看右孩子是否存在，不存在返回上一级，存在就输出
}
void Qpreshowtree(RTree* st)//前序输出调用
{
	if(!st) return;
	printf("前续遍历结果：");
	Qprinttree(st->root);
	putchar('\n');
}

//中序遍历
void Zprinttree(BTNode* tp)//中序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	Zprinttree(tp->lchild);//看根的左孩子，如果左孩子存在,那么继续找左孩子的左孩子
	printf("%d ",tp->val);//左孩子不存在，则返回上一级输出根数据
	Zprinttree(tp->rchild);//再看这个根的右孩子，如果右孩子存在,那么继续找右孩子的左孩子
}
void Zpreshowtree(RTree* st)//中序输出调用
{
	if(!st) return;
	printf("中续遍历结果：");
	Zprinttree(st->root);
	putchar('\n');
}

//后序遍历,先叶子后节点
void Hprinttree(BTNode* tp)//后序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	Hprinttree(tp->lchild);//看根的左孩子
	Hprinttree(tp->rchild);//再看这个根的右孩子
	printf("%d ",tp->val);//左右孩子都不存在，说明这是叶子，则输出数据
}
void Hpreshowtree(RTree* st)//后序输出调用,
{
	if(!st) return;
	printf("后续遍历结果：");
	Hprinttree(st->root);
	putchar('\n');
}

//层序遍历
void Cprinttree(BTNode* tp)//tp指向节点
{
	BTNode* queue[20]={0};//定义一个队列（结构体指针数组），用来存放节点结构体的地址
	BTNode* cur=NULL;//存放出队的节点地址（数组元素）
	int head=-1,rear=-1;//初始化队列，空队列head=rear
	queue[++rear]=tp;//将根入队
	while(head!=rear)//如果队列不为空则
	{
		cur=queue[++head];//将队头节点出队赋给cur
		printf("%d ",cur->val);//输出节点数据
		if(cur->lchild)//判断节点是否有左孩子
		{
			queue[++rear]=cur->lchild;//有则入队
		}
		if(cur->rchild)//判断节点是否有右孩子
		{
			queue[++rear]=cur->rchild;//有则入队
		}
	}
}
void Cpreshowtree(RTree* st)//层序遍历调用
{
	if(!st) return;
	printf("层序遍历结果：");
	Cprinttree(st->root);//将树的根地址作为参数
	putchar('\n');
}

7、主函数

void main()
{
	int arr[maxsize]={3,1,2,5,4,7,9};//树的数据
	BTNode* tp=NULL;//新的节点
	RTree* st=NULL;//根节点
	int bl=-1;//树空的判断
	st=Init();//维护结构初始化
	inserArrBTree(st,arr,maxsize);//层序建树
	printf("树的节点数为：%d\n",st->num);
	putchar('\n');
	Qpreshowtree(st);//前序输出
	Zpreshowtree(st);//中序输出
	Hpreshowtree(st);//后续输出
	Cpreshowtree(st);//层序输出
	putchar('\n');

	//cleartree(st);//清空树
	//if(st->num==0)printf("清空完成\n");
	//putchar('\n');

	tp=findtree(st,1);
	printf("查找树：");
	if(tp==NULL)
	{
		printf("查找失败!\n");
	}
	else
		printf("查找成功!\n");
	putchar('\n');

	printf("树的高度为：%d\n",gaodu(st));
	putchar('\n');

	/*bl=treenull(st);
	if(bl==0)printf("树为空\n");
	if(bl==1)printf("树不为空\n");
	putchar('\n');*/
}

三、总代码

#include<stdio.h>
#include <stdlib.h> 
#define maxsize 7//数组的最大容量maxsize

//树的节点结构
typedef struct treeNode
{
	int val;//数据域
	struct treeNode *lchild,*rchild;//左孩子右孩子，指针域
}BTNode;

//树的维护结构
typedef struct
{
	int num;//计数
	BTNode *root;//根节点
}RTree;

//对维护结构的初始化
RTree* Init()
{
 	RTree *st=(RTree*)malloc(sizeof(RTree));
	st->num=0;
	st->root=NULL;
	return st;
}

//判断树空
int treenull(RTree* tp)
{
	return (!tp) ? 0 : ((!tp->num) ? 0 : 1); 
}

//树的高度
int gaodufuzhu(BTNode* s)//树高度的计算辅助函数
{
	int left=0,right=0;//左右的高度
	if(!s)return 0;
	left=gaodufuzhu(s->lchild);
	right=gaodufuzhu(s->rchild);
	return (left>right) ? left+1 : right+1;//三目运算，left>right时返回left+1，否则left<right时返回right+1
}
int gaodu(RTree* tp)//树高度的计算调用函数
{
	if(!tp)return 0;
	return gaodufuzhu(tp->root);
}

//新建树（层序建立）
void inserArrBTree(RTree *st,int *arr,int n)//插入树（树维护的地址，要插入的数组地址，要插入的数组元素的个数）
{
	int i=1;//数组的下标指针
	int head,rear;//定义队的头尾指针
	BTNode* queue[20]={0};//创建一个队列（用结构体指针数组实现，用来存放节点的指针）
	BTNode* cur;//出队的指针存储
	if(!st) return;
	if(st->root==NULL)//如果是第一个根节点则：
	{
		st->root=(BTNode*)malloc(sizeof(BTNode));//申请节点的内存空间赋给根节点
		st->root->lchild=st->root->rchild=NULL;//将节点的左右孩子都置为空
		st->root->val=arr[0];//将数组第一个数据存入根节点的数据域,往后的数据从i=1开始，到n-1结束
		st->num++;
	}

	//指针队列初始化
	head=-1;//头指针处没有数据的(参见队列的内容)
	rear=-1;//初始化队列，空队列head=rear
	queue[++rear]=st->root;//将根节点入队
		
	while(i<n)
	{
		cur=queue[++head];//队头（下标小的）出队
		
		if(cur->lchild)//左孩子如果不为空有节点
		{
			queue[++rear]=cur->lchild;//将这个节点入队
			st->num++;
		}
		else//左孩子如果为空没有节点
		{
			cur->lchild=(BTNode*)malloc(sizeof(BTNode));//申请新节点的内存和初始化
			cur->lchild->lchild=cur->lchild->rchild=NULL;
			cur->lchild->val=arr[i++];//将数组元素放入新的节点
			queue[++rear]=cur->lchild;
			st->num++;
		}

		if(i==n)break;//如果数组待处理的元素没有了，则返回

		if(cur->rchild)//右孩子如果不为空有节点
		{
			queue[++rear]=cur->rchild;//将这个节点入队
			st->num++;
		}
		else//右孩子如果为空没有节点
		{
			cur->rchild=(BTNode*)malloc(sizeof(BTNode));//申请新节点的内存和初始化
			cur->rchild->lchild=cur->rchild->rchild=NULL;
			cur->rchild->val=arr[i++];//将数组元素放入新的节点
			queue[++rear]=cur->rchild;
			st->num++;
		}
	}	
}

//清空树
int clearfuzhu(BTNode* tp,int *n)//-1(空)，n为 计数变量的地址
{
	int left,right;
	if(!tp) 
		return -1;
	left=clearfuzhu(tp->lchild,n);//递归算法
	right=clearfuzhu(tp->rchild,n);
	if((left==right)==-1);
	{
		free(tp);
		(*n)--;//*指针取值符，取出计数单位进行减操作
		return -1;
	}
	return 0;
}
int cleartree(RTree* st)//清空树的调用
{
	if(!st || !(st->num)) return 0;
	return clearfuzhu(st->root,&(st->num));//st->root是根节点的地址，&(st->num)是计数变量的地址
}

//查找树的数据是否存在
BTNode* fuzhufind(BTNode* tp,int n)//返回的是一个节点的地址，n代表要查找的数据
{
	BTNode *left,*right;//定义左树根的地址（广义的根）和右树的根的地址（广义的根）
	if(!tp)return NULL;//判断广义节点是否为空
	if(tp->val==n)//广义节点部位空，查验此时的广义根的数据是否等于我们要找的数据
		return tp;//如果等于则返回这个广义节点的地址
	left=fuzhufind(tp->lchild,n);//若不等于则继续对这个广义节点的左孩子递归
	right=fuzhufind(tp->rchild,n);//左孩子结束后对右孩子递归
	return left ? left : (right ? right : NULL);//三目运算符，a？b:c--如果a为真则b执行，否则c执行
												//如果是在树的左边找到的，则返回左值，否则返回右值，没有找到返回NULL
}
BTNode* findtree(RTree* st,int n)//查找调用（根节点的地址，查找的数值），返回的是一个节点的地址
{
	if(!st) return NULL;//如果根节点为空，则返回空
	return fuzhufind(st->root,n);//调用查找的辅助函数并返回节点的地址
}




//前序遍历
void Qprinttree(BTNode* tp)//前序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	printf("%d ",tp->val);//输出根数据
	Qprinttree(tp->lchild);//看根的左孩子，如果左孩子存在，则输出，否则左孩子为空，则返回上一级
	Qprinttree(tp->rchild);//返回上一级后再看右，同样的，看右孩子是否存在，不存在返回上一级，存在就输出
}
void Qpreshowtree(RTree* st)//前序输出调用
{
	if(!st) return;
	printf("前续遍历结果：");
	Qprinttree(st->root);
	putchar('\n');
}

//中序遍历
void Zprinttree(BTNode* tp)//中序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	Zprinttree(tp->lchild);//看根的左孩子，如果左孩子存在,那么继续找左孩子的左孩子
	printf("%d ",tp->val);//左孩子不存在，则返回上一级输出根数据
	Zprinttree(tp->rchild);//再看这个根的右孩子，如果右孩子存在,那么继续找右孩子的左孩子
}
void Zpreshowtree(RTree* st)//中序输出调用
{
	if(!st) return;
	printf("中续遍历结果：");
	Zprinttree(st->root);
	putchar('\n');
}

//后序遍历,先叶子后节点
void Hprinttree(BTNode* tp)//后序遍历递归（自动）
{
	if(!tp) return;//tp指向的是根节点(广义的根节点，把树细分蔚多个子树)
	Hprinttree(tp->lchild);//看根的左孩子
	Hprinttree(tp->rchild);//再看这个根的右孩子
	printf("%d ",tp->val);//左右孩子都不存在，说明这是叶子，则输出数据
}
void Hpreshowtree(RTree* st)//后序输出调用,
{
	if(!st) return;
	printf("后续遍历结果：");
	Hprinttree(st->root);
	putchar('\n');
}

//层序遍历
void Cprinttree(BTNode* tp)//tp指向节点
{
	BTNode* queue[20]={0};//定义一个队列（结构体指针数组），用来存放节点结构体的地址
	BTNode* cur=NULL;//存放出队的节点地址（数组元素）
	int head=-1,rear=-1;//初始化队列，空队列head=rear
	queue[++rear]=tp;//将根入队
	while(head!=rear)//如果队列不为空则
	{
		cur=queue[++head];//将队头节点出队赋给cur
		printf("%d ",cur->val);//输出节点数据
		if(cur->lchild)//判断节点是否有左孩子
		{
			queue[++rear]=cur->lchild;//有则入队
		}
		if(cur->rchild)//判断节点是否有右孩子
		{
			queue[++rear]=cur->rchild;//有则入队
		}
	}
}
void Cpreshowtree(RTree* st)//层序遍历调用
{
	if(!st) return;
	printf("层序遍历结果：");
	Cprinttree(st->root);//将树的根地址作为参数
	putchar('\n');
}

void main()
{
	int arr[maxsize]={3,1,2,5,4,7,9};//树的数据
	BTNode* tp=NULL;//新的节点
	RTree* st=NULL;//根节点
	int bl=-1;//树空的判断
	st=Init();//维护结构初始化
	inserArrBTree(st,arr,maxsize);//层序建树
	printf("树的节点数为：%d\n",st->num);
	putchar('\n');
	Qpreshowtree(st);//前序输出
	Zpreshowtree(st);//中序输出
	Hpreshowtree(st);//后续输出
	Cpreshowtree(st);//层序输出
	putchar('\n');

	//cleartree(st);//清空树
	//if(st->num==0)printf("清空完成\n");
	//putchar('\n');

	tp=findtree(st,1);
	printf("查找树：");
	if(tp==NULL)
	{
		printf("查找失败!\n");
	}
	else
		printf("查找成功!\n");
	putchar('\n');

	printf("树的高度为：%d\n",gaodu(st));
	putchar('\n');

	/*bl=treenull(st);
	if(bl==0)printf("树为空\n");
	if(bl==1)printf("树不为空\n");
	putchar('\n');*/
}