java数据结构 二叉树查找

二叉查找树

二叉查找树，又称二叉排序树，具有如下性质

• 若它的左子树不为空，则左子树上所有
• 结点的值均小于它的根结构的值
• 若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值
• 它的左、右子树也分别为二叉排序树

//树的结点类
public class TreeNode<T> {
    //存储数据
    public T data;
    //指向左孩子和右孩子结点
    public TreeNode<T> left,right;
    public TreeNode(T data, TreeNode<T> left, TreeNode<T> right) {
        super();
        this.data = data;
        this.left = left;
        this.right = right;
    }
    public TreeNode(T data) {
        super();
        this.data = data;
    }
    public TreeNode() {
        this.data = null;
        this.left = null;
        this.right =null;   
    }

    public String toString() {
        return this.data.toString();
    }   
}

//我们使用泛型保证传入的对象必须具有比较的性质
public class BinarySearchTree<T extends Comparable> {
    public TreeNode<T> root;

    public BinarySearchTree() {
        super();
    }

    public BinarySearchTree(T x) {
        super();
        root=new TreeNode<>(x);
    }

    //判断该树是否为空
    public boolean isEmpty() {
        return root==null;
    }

    public boolean contains(T x) {
        return contains(x,root);
    }
    //判断当前树是否包含某个对象，对象必须实现Comparable接口或者手动实现比较器，使用递归来完成
    public boolean contains(T x,TreeNode<T> root) {
        if(root==null) {
            return false;
        } 

        int result=x.compareTo(root.data);
        if(result<0) {
            return contains(x,root.left); 
        }else if(result >0) {
            return contains(x,root.right);
        }else{
            return true;
        }
    } 

    public T findMax() {
        return findMax(root);
    }
    //查找最大值
    public T findMax(TreeNode<T> root)
    {
        if(root==null) {
            return null;
        }else if(root.right==null) {
            return root.data;
        }
        return findMax(root.right);
    } 

    public T findMin() {
        return findMin(root);
    }

    //查找最小值
    public T findMin(TreeNode<T> root) {
        if(root==null) {
            return null;
        }else if(root.left==null) {
            return root.data;
        }

        return findMin(root.left);
    } 

    public void insert(T x) {
        if(root==null) {
            this.root=insert(x,this.root);
        }else {
            insert(x,this.root);
        }
    }

    //插入操作
    public TreeNode insert(T x,TreeNode root) {
        if(root==null) {
            return new TreeNode(x,null,null);  
        }

        int result =x.compareTo(root.data);
        if(result<0) {
            root.left=insert(x,root.left);
        }else if(result>0){
            root.right=insert(x,root.right);
        }   
        return root;
    }


    public void remove(T x) {
        remove(x,root);
    }

    //删除操作
    /*删除操作比较麻烦，因为需要考虑好几种情况
    *1.删除的是叶子结点，直接删除
    *2.删除的有一个子结点，可以直接将其子结点移动到这个位置
    *3.如果有两个结点，我们也可以先让左子树移动到当前位置，然后对右子树重新排序，但是这个方法效率很低。
    *  所以我们可以找到一个替代该结点的结点，这个结点就是右子树的最小结点，这样整棵树的结构不会有任何变化
    */
    public TreeNode<T> remove(T x,TreeNode<T> root) {
        if(root==null) {
            return null;
        }
        int result=x.compareTo(root.data);

        if(result<0) {
            remove(x,root.left);
        }else if(result>0) {
            remove(x,root.right);
        }else if(root.left!=null&&root.right!=null) {
            root.data=findMin(root.right);
            root.right=remove(root.data,root.right);
        }else {
            root=(root.left!=null)?root.left:root.right;
        }
        return root;
    }
      public  void preOrder(TreeNode<T> p) {
            if (p != null) {
                // 访问当前结点
                System.out.print(p.data.toString() + " ");
                // 按先根次序遍历当前结点的左子树，递归调用
                preOrder(p.left);
                // 按先根次序遍历当前结点的右子树，递归调用
                preOrder(p.right);
            }
       }
}

虽然二叉查找树查询插入等平均操作效率都有提高，但是有一些很特别的情况，我们来考虑一下 。

例如有一个已排好序的数组{35，37，47，51，58，62，73，88，93，99}，那么我们插入这些元素构成的二叉排序树如下图

AVL树

AVL树是i带有平衡条件的二叉排序树，一棵AVL树其每一个结点的左子树和右子树的高度最多差一。我们将二叉树结点的左子树深度减去右子树深度的值称为平衡因子BF，AVL树上所有结点的平衡因子只可能是-1、0、1.加粗样式
如下图，图1是平衡二叉树。图二不是，因为平衡二叉树的前提首先是一棵二叉排序树。图三不是平衡二叉树的原因是结点58的左子树高度为2，右子树为空，BF大于1，所以不平衡。

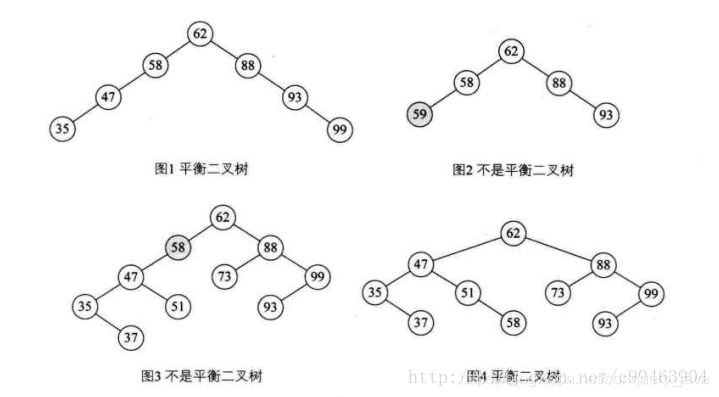
距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。

如下图，当新插入结点37时，距离它最近的平衡因子绝对值超过1的结点是58，所以从58开始以下的子树为最小不平衡子树

平衡二叉树实现

//平衡二叉树的结点类

public class AvlNode<T> { 
    //结点的数据
    T element;
    //指向其左右孩子
    AvlNode<T> left,right;
    //高度
    int height;
    public AvlNode() {
        super();
    }
    public AvlNode(T element, AvlNode<T> left, AvlNode<T> right, int height) {
        super();
        this.element = element;
        this.left = left;
        this.right = right;
        this.height = height;
    }
    public AvlNode(T element) {
        super();
        this.element = element;
    }

    //返回树的高度
    public int getHeight(AvlNode<T> t) {
        return t==null?-1:height;
    }
}

public class AvlTree<T extends Comparable> {
    //根结点
    AvlNode<T> root;

    public AvlTree() {
        super();
    }

    //获取树的高度
    public int getHeight(AvlNode<T> t) {
        if(t!=null)
            return t.getHeight(t);
        return -1;
    }

    //先序遍历平衡二叉树 
   public void preOrder(AvlNode<T> p) {
        if (p != null) {
            // 访问当前结点
            System.out.print(p.element.toString() + " ");
            // 按先根次序遍历当前结点的左子树，递归调用
            preOrder(p.left);
            // 按先根次序遍历当前结点的右子树，递归调用
            preOrder(p.right);
        }
    }
    //插入操作
    public void insert(T value) {
            root=insert(value,root);
    }

    public AvlNode<T> insert(T value,AvlNode<T> tree){
        if(tree==null)
            return new AvlNode<T>(value);
        int result=value.compareTo(tree.element);

        if(result>0) {
            tree.right=insert(value,tree.right);
        }else if(result<0) {
            tree.left=insert(value,tree.left);
        }

        //平衡二叉树
        return balance(tree);   
    }
    //左旋操作
    private AvlNode<T> rotateWithRightChild(AvlNode<T> p){
        AvlNode<T> k1=p.left;
        p.left=k1.right;
        k1.right=p;
        p.height=Math.max(getHeight(p.left), getHeight(p.right))+1;
        k1.height=Math.max(getHeight(k1.left), p.height)+1;
        return k1;
    }
    /**
     * 右旋操作
     * 
     * 
     */
    private AvlNode<T> rotateWithLeftChild(AvlNode<T> p){
        AvlNode<T> k1=p.right;
        p.right=k1.left;
        k1.left=p;
        p.height=Math.max(getHeight(p.left), getHeight(p.right))+1;
        k1.height=Math.max(getHeight(k1.right), p.height)+1;
        return k1;
    }

    //双旋转操作
    public AvlNode<T> doubleWithLeftChild(AvlNode<T> k){
        k.left=rotateWithLeftChild(k.left);
        return rotateWithRightChild(k);
    }
    //双旋转操作
    public AvlNode<T> doubleWithRightChild(AvlNode<T> k){
        k.right=rotateWithRightChild(k.right);
        return rotateWithLeftChild(k);
    }

    //平衡二叉树操作
    public AvlNode<T> balance(AvlNode<T> t){ 
        //当左子树比右子树高度大于1时，左旋转
        if(getHeight(t.left)-getHeight(t.right)>1) { 
            //判断需要单旋转还是双旋转
            if(getHeight(t.left.left)>=getHeight(t.left.right)) {
                t=rotateWithRightChild(t);
            }else {
                t=doubleWithLeftChild(t);
            }
        }
        //当右子树比左子树高度大于1时，右旋转
        else if(getHeight(t.right)-getHeight(t.left)>1) {
            if(getHeight(t.right.right)>=getHeight(t.right.left)) {
                t=rotateWithLeftChild(t);
            }else {
                t=doubleWithRightChild(t);
            }
        }
        t.height=Math.max(getHeight(t.left), getHeight(t.right))+1;
        return t;

    }

    public AvlNode<T> remove(T x){
        return remove(x,root);
    }

    //删除操作
    public AvlNode<T> remove(T x,AvlNode<T> t){
        if(t==null) {
            return null;
        }

        int result=x.compareTo(t.element);
        if(result>0) {
            t.right=remove(x,t.right);
        }else if(result<0) {
            t.left=remove(x,t.left);
        }else if(t.left!=null&&t.right!=null) {
            t.element=findMin(t.right);
            t.right=remove(t.element,t.right);
        }else {
          t=(t.left!=null)?t.left:t.right;
        } 
        if(t==null) {
            return null;
        }
        return balance(t);
    }
    //查找最小值
    public T findMin(AvlNode<T> root) {
        if(root==null) {
            return null;
        }else if(root.left==null) {
            return root.element;
        }

        return findMin(root.left);
    } 
}