初始PyTorch
pytorch是一个基于Python的科学计算包。
Pytorch是动态图优先，例如下图：
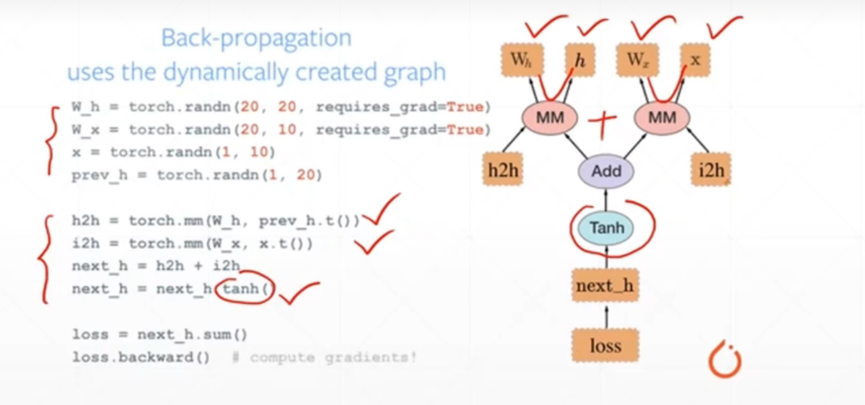
计算图的搭建和运算是同时的，随时可以输出结果,因此非常的直观和易于调试。
Pytorch可以做什么：
- GPU加速
import torch
import time
print(torch.__version__)
print("gpu:", torch.cuda.is_available())
# a是10000*1000的矩阵
a = torch.randn(10000, 1000)
# b是1000*2000的矩阵
b = torch.randn(1000, 2000)
# 在CPU上运行
t0 = time.time()
# 做矩阵乘法
c = torch.matmul(a, b)
t1 = time.time()
print(a.device, t1 - t0, c.norm(2))
# 使用cuda，此次运行时间可能比上面长，因为第一次需要完成初始化
device = torch.device('cuda')
a = a.to(device)
b = b.to(device)
# 使用cuda运行的真实时间，明显比第一个快
t0 = time.time()
c = torch.matmul(a, b)
t2 = time.time()
print(a.device, t2 - t0, c.norm(2))
t0 = time.time(
c = torch.matmul(a, b)
t1 = time.time()
print(a.device, t1 - t0, c.norm(2))
- 自动求导
import torch
from torch import autograd
x = torch.tensor(1.)
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)
y = a ** 2 * x + b * x + c
# 求导前a的梯度，b的梯度，c的梯度
print('before:', a.grad, b.grad, c.grad)
# y对a求导，y对b求导，y对c求导
grads = autograd.grad(y, [a, b, c])
print('after:', grads[0], grads[1], grads[2])
- 常用网络层
PyTorch入门
tensor
Tensor类似于Numpy的ndarray，但是可以用GPU加速，使用前需要导入torch包。
import torch
x = torch.empty(5, 3) # 构建5*3的未初始化的矩阵
print(x)
import torch
x = torch.zeros(5, 3, dtype=torch.long) # 构造一个5*3的元素全为0的并且元素类型为long的矩阵
print(x)
用已有的tensor来构建tensor，还可以改变type.
import torch
x = torch.zeros(5, 3, dtype=torch.long)
y = x.new_ones(5, 3, dtype=torch.double)
print(y)
import torch
x = torch.zeros(5, 3, dtype=torch.long)
print(x)
y = torch.randn_like(x, dtype=torch.float) # 构建与x同维的矩阵y
print(y)
可以使用x.size()查看矩阵x的shape。
x.size()返回的是torch.size,torch.size是turple
operation
peration一般可以使用函数的方式使用，但是为了方便使用，PyTorch中重载一些运算符，例如：
两个矩阵相加（必须同维)
import torch
x = torch.rand(5, 3)
print(x)
y = torch.rand(5, 3)
print(y)
print(x + y)
也可以使用函数add
import torch
x = torch.rand(5, 3)
print(x)
y = torch.rand(5, 3)
print(y)
print(torch.add(x, y))
tensor的变换
可以像使用numpy的下标运算来操作PyTorch的tensor
import torch
x = torch.rand(3, 3)
print(x)
print(x[:, 1]) # 打印x中的第一列（下标从0开始）
可以使用view函数来resize或者reshape一个tensor
import torch
x = torch.randn(4, 4)
print(x)
y = x.view(16) # y就是有16个元素的一维矩阵
print(y)
import torch
x = torch.randn(4, 4)
print(x)
y = x.view(-1, 8) # -1表示自己判断自己的维数
print(y)
如果tensor中只有一个元素，可以通过item函数将它变成一个数
import torch
x = torch.randn(1)
print(x)
print(x.item())
Tensor与Numpy的互相转换
它们会共享内存地址，因此修改一方会影响另一方。
Tensor转numpy，直接使用numpy函数
import torch
a = torch.ones(5, 3)
print(a)
b = a.numpy()
print(b)
Numpy转为tensor
import torch
import numpy as np
a = np.ones(5)
print(a)
b = torch.from_numpy(a)
print(b)
Tensor在GPU与CPU上切换
Tensor可以在创建时指定device类型，也可以使用to函数来移动到任意设备上
import torch
import numpy as np
# 如果有CUDA，可以把tensor放在GPU上
x = torch.rand(3, 2)
if torch.cuda.is_available():
device = torch.device('cuda') # 创建一个cuda device对象
y = torch.ones_like(x, device=device) # 直接在GPU上创建一个和x同维的矩阵y
x = x.to(device) # 使用to将x从cpu移到GPU
z = x + y
print(z)
Autograd: 自动求导
PyTorch的核心是autograd包。autograd为所有用于Tensor的operation提供自动求导的功能。
torch.Tensor 是这个包的核心类。如果它的属性requires_grad是True，那么PyTorch就会追踪所有与之相关的operation。当完成(正向)计算之后， 我们可以调用backward()，PyTorch会自动的把所有的梯度都计算好。与这个tensor相关的梯度都会累加到它的grad属性里。
如果不想计算这个tensor的梯度，我们可以调用detach()，这样它就不会参与梯度的计算了。
为了阻止PyTorch记录用于梯度计算相关的信息(从而节约内存)，我们可以使用 with torch.no_grad()。这在模型的预测时非常有用，因为预测的时候我们不需要计算梯度，否则我们就得一个个的修改Tensor的requires_grad属性，这会非常麻烦。
关于autograd的实现还有一个很重要的Function类。Tensor和Function相互连接从而形成一个有向无环图, 这个图记录了计算的完整历史。每个tensor有一个grad_fn属性来引用创建这个tensor的Function(用户直接创建的Tensor，这些Tensor的grad_fn是None)。
如果你想计算梯度，可以对一个Tensor调用它的backward()方法。如果这个Tensor是一个scalar(只有一个数)，那么调用时不需要传任何参数。如果Tensor多于一个数，那么需要传入和它的shape一样的参数，表示反向传播过来的梯度。
创建tensor时设置属性requires_grad=True，PyTorch就会记录用于反向梯度计算的信息：
import torch
x = torch.ones(3, 2, requires_grad=True)
print(x)
通过operation产生新的tensor的grad_fn不是None
可以通过requires_grad_()函数会修改一个Tensor的requires_grad
import torch
a = torch.randn(3, 2)
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
现在我们反向计算梯度
使用backward()求导
import torch
x = torch.ones(2, 2, requires_grad=True)
y = x + 2 # x中的各个元素加2，并赋值给y
z = y * y * 3 # y中的每个元素平方*3，并赋值给z
out = z.mean() # 求z矩阵所有元素的平均值，并赋值给out，所以out是一个数
out.backward()
print(x.grad) # 打印out对x的偏导
补充：
0范数： 向量中非零元素的个数。
1范数： 为绝对值之和。
2范数： 通常意义上的模。
无穷范数：取向量的最大值。
在pytorch的计算图里只有两种元素：数据（tensor）和 运算（operation）
运算包括了：加减乘除、开方、幂指对、三角函数等可求导运算
数据可分为：叶子节点（leaf node）和非叶子节点；叶子节点是用户创建的节点，不依赖其它节点；它们表现出来的区别在于反向传播结束之后，**非叶子节点的梯度会被释放掉，只保留叶子节点的梯度，**这样就节省了内存。如果想要保留非叶子节点的梯度，可以使用retain_grad()方法。
使用backward()函数反向传播计算tensor的梯度时，并不计算所有tensor的梯度，而是只计算满足这几个条件的tensor的梯度：
1.类型为叶子节点
2.requires_grad=True
3.依赖该tensor的所有tensor的requires_grad=True。
所有满足条件的变量梯度会自动保存到对应的grad属性里。
例如：y=(x+1)*(x+2)，当x=2时，计算y对x的导数
import torch
x = torch.tensor(2., requires_grad=True) # 叶子结点
a = torch.add(x, 1) # 非叶子结点
b = torch.add(x, 2) # 非叶子结点
y = torch.mul(a, b) # 非叶子结点
y.backward()
print(x.grad) # y对x的导数
使用autograd求导
import torch
x = torch.tensor(2., requires_grad=True)
a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)
grad = torch.autograd.grad(outputs=y, inputs=x)
print(grad[0])
因为指定了输出y，输入x，所以返回值就是y对x的导数，返回值其实是一个只有一个元素的元组。
求一阶导可以用backward()
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
z.backward()
print(x.grad)
print(y.grad)
也可以用autograd.grad()
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
# 需要添加retain_graph=True,避免被释放
grad_x = torch.autograd.grad(outputs=z, inputs=x, retain_graph=True)
grad_y = torch.autograd.grad(outputs=z, inputs=y)
print(grad_x[0], grad_y[0]) # 输出z对x的偏导，z对y的偏导
在计算高阶导时需要使用creat_graph=True在保留原图的基础上再建立额外的求导计算图
方法1：
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
grad_x = torch.autograd.grad(outputs=z, inputs=x, create_graph=True)
grad_y = torch.autograd.grad(outputs=z, inputs=y)
print(grad_x[0], grad_y[0])
grad_xx = torch.autograd.grad(outputs=grad_x, inputs=x)
print(grad_xx[0]) # 输出z对x的二阶导
方法2：
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
grad_x = torch.autograd.grad(outputs=z, inputs=x, create_graph=True)
grad_y = torch.autograd.grad(outputs=z, inputs=y)
grad_x[0].backward() # 从grad_x开始回传
print(x.grad)
方法3：使用两次backward()
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
z.backward(create_graph=True)
x.grad.backward()
print(x.grad)
输出是18，而不是6，这是因为**PyTorch****使用backward()**时默认会累加梯度，需要手动把前一次的梯度清零。
import torch
x = torch.tensor(2.).requires_grad_(True)
y = torch.tensor(3.).requires_grad_(True)
z = x * x * y
z.backward(create_graph=True)
x.grad.data.zero_() # 梯度清0
x.grad.backward()
print(x.grad)
需要注意的是：PyTorch****中只能标量对标量或者标量对向量求梯度
如果y是向量，需要先将y转变为标量，
方法1是对y的各个元素求和，然后再分别求导。
例如：
import torch
x = torch.tensor([1., 2.], requires_grad=True)
y = x * x
y.sum().backward()
print(x.grad)
方法2：使用grad_tensors参数。
torch.autograd.backward(
tensors, # 要计算导数的张量 torch.autograd.backward(tensor)和tensor.backward()作用是等价的
grad_tensors=None, # 在用非标量进行求导时需要使用该参数
retain_graph=None, # 保留计算图
create_graph=False,
grad_variables=None)
使用grad_tensors参数：
它是非标量(y)进行求导时才使用
它的大小需要与张量y(y=f(x))的大小相同
它在每一个元素是全1是就是正常的求导
可以调整它的值来针对每一项在求导时占据的权重。
import torch
x = torch.randn(3, 3, requires_grad=True)
y = x * x
grad_tensors = torch.ones_like(y)
y.backward(grad_tensors)
print(x.grad)
方法3：使用autogard
import torch
x = torch.randn(3, 3, requires_grad=True)
print(x)
y = x * x
grad_x = torch.autograd.grad(outputs=y, inputs=x,
grad_outputs=torch.ones_like(y))
print(grad_x[0])
扫一扫
1271
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
