Pytorch中使用backward()求导详解

最新推荐文章于 2025-02-23 15:37:35 发布

原创最新推荐文章于 2025-02-23 15:37:35 发布 · 8.9k 阅读

77 ·

CC 4.0 BY-SA版权

深度学习相关专栏收录该内容

14 篇文章

订阅专栏

本文详细解析了Pytorch中backward()方法的三种使用场景，包括标量、向量及矩阵输出的梯度计算过程，并通过具体代码示例展示了如何在不同情况下求取张量的偏导数。

部署运行你感兴趣的模型镜像

backward()是Pytorch中用来求梯度的方法，可以分为三种情况来使用。

1.out.backwark()中out是一个标量

此时可以直接使用out.backwark():

import torch
from torch.autograd import Variable

#生成一个内容为[2,3]的张量，Varibale 默认是不要求梯度的，如果要求梯度，
#需要加上requires_grad=True来说明
#这里的Variable是为了设置变量，把a0=2,a1=3设置为两个变量
a = Variable(torch.tensor([2,3]),requires_grad=True)
b = a+3
c = b*3
out=c.mean() #求均值
out.backward()
print("a=",a)
print("out=",out)
print(a.grad)  #求out对a的偏导

结果为

a= tensor([2., 3.], requires_grad=True)
out= tensor(16.5000, grad_fn=<MeanBackward0>)
tensor([1.5000, 1.5000])

将上面的程序写成数学表达式就是：
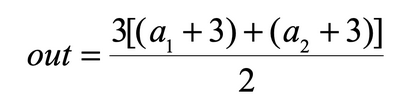
在这里插入图片描述
求偏导的过程为：

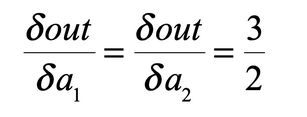
2. out.backward()中的out是一个向量（或者理解成1xN的矩阵）

import torch
from torch.autograd import Variable

#生成一个内容为[2,4]的张量，Varibale 默认是不要求梯度的，如果要求梯度，
#需要加上requires_grad=True来说明
a = Variable(torch.Tensor([[2,4]]),requires_grad=True)
b = torch.zeros(1,2)
b[0,0] = a[0,0]**2+a[0,1]
b[0,1] = a[0,1]**3+a[0,0]
out = 2*b

#括号里面的参数要传入和out维度一样的矩阵
#这个矩阵里面的元素会作为最后加权输出的权重系数
out.backward(torch.FloatTensor([[1,2]]))
print("a=",a)
print("out=",out)
print(a.grad)  #求out对a的偏导

结果为：

a= tensor([[2., 4.]], requires_grad=True)
out= tensor([[ 16., 132.]], grad_fn=<MulBackward0>)
tensor([[12., 194.]])

将上面的程序写成数学表达式就是：
$a_0=2,a_1=4$
$b_0=a_0^2+a_1$
$b_1=a_0+a_1^3$
$out_0=2b_0=2a_0^2+2a_1$
$out_1=2b_1=2a_0+2a_1^3$
$∂out∂a=[∂out0∂a0∂out0∂a1∂out1∂a0∂out1∂a1]=[82296]\frac{\partial out}{\partial a}=\begin{bmatrix} \frac{\partial out_0}{\partial a_0} &\frac{\partial out_0}{\partial a_1} \\ \frac{\partial out_1}{\partial a_0}& \frac{\partial out_1}{\partial a_1} \end{bmatrix}=\begin{bmatrix} 8 & 2 \\ 2 & 96 \end{bmatrix}$
这儿有个疑问，为什么上面的程序计算出来是[12,194]呢？大家可以看到这一行传进去的两个参数[1,2]

out.backward(torch.FloatTensor([[1,2]]))

有：
$[12]∗[82296]=[12194]\begin{bmatrix} 1 & 2 \end{bmatrix}*\begin{bmatrix} 8 & 2 \\ 2 & 96 \end{bmatrix}=\begin{bmatrix} 12 & 194 \end{bmatrix}$

3. out.backward()中的out是一个矩阵

import torch
from torch.autograd import Variable

#生成一个内容为[2,3]的张量，Varibale 默认是不要求梯度的，如果要求梯度，
#需要加上requires_grad=True来说明
a = Variable(torch.Tensor([[2,3],[1,2]]),requires_grad=True)
w = Variable(torch.ones(2,1),requires_grad=True)
out = torch.mm(a,w)

#括号里面的参数要传入和out维度一样的矩阵
#这个矩阵里面的元素会作为最后加权输出的权重系数
out.backward(torch.FloatTensor([[1],[1]]))
print("gradients are:{}".format(w.grad.data))

结果为：

gradients are:tensor([[3.],
        [5.]])

您可能感兴趣的与本文相关的镜像

PyTorch 2.8

PyTorch

Cuda

PyTorch 是一个开源的 Python 机器学习库，基于 Torch 库，底层由 C++ 实现，应用于人工智能领域，如计算机视觉和自然语言处理