Android应用风格不应照抄iOS

苹果iOS平台上之所以有这么优秀的应用，主要得益于苹果官方有一套非常成熟的UI套件和人机交互手册来指导第三方开发者。这样即便你对产品设计、UI交互什么都不懂，按照苹果的官方手册来，也能做出一个看起来不错的App。

但Android上就不一样了，Android 4.x之前，Google 对应用开发市场没有一个统一和严格的标准，导致Android应用良莠不齐。但Android 4.0之后，Google 开始重视UI设计了，并于去年一月份推出了Android Design 官方指导网站，提供了比较完整的指导方案和大量Android 模块。

到目前为止，Android Design 诞生已经一年有余，这中间也出现了很多按照Android Design设计的优秀App。但相比于大部分App(尤其是国内和官方日益分裂的Android市场)，有类Holo主题的Android Design App还是极少数的。大部分都是将iOS上的那套UI直接搬过来，不仅体验、交互有很大的问题，同时在Android 4.x的系统下也显得丑陋不堪。

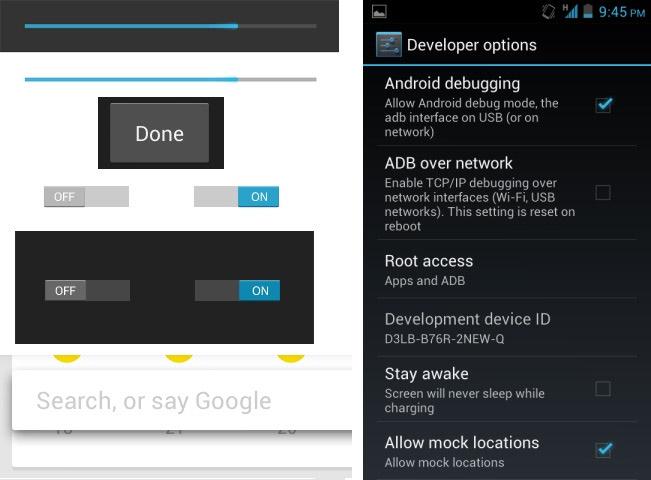
我之前在多篇文章中提到过，Android、iOS、WP这三个系统平台的设计语言和理念完全不同。iOS是将其拟物化风格不断地放大，尽可能的模拟现实 生活和模仿用户最自然的交互方式，并在其优质的屏幕和触摸体验下尽量的把学习成本降到最低。Win8和WP则是采用名为Modern的贴片风格，将所有外在形式的东西尽可能的压缩，把内容凸显出来，以扁平化的设计理念让内容的布局和呈现都实现了一种质的突破。虽然其简陋的界面和稍有复杂的手势操作会让学习 和适应成本升高，但其突破性的设计理念仍然吸引了业内大量的借鉴和模仿。

而Android 的设计又和上面两个完全不同。从内容表现形式上来看，Android 偏向于Win8的扁平化风格，但它又在细节之处运用了很多仿真的效果。比如在按钮、键盘或卡片分层上，都会有一到两排的像素差异，做出高光和立体的效果; 而在设置界面的控制按钮上，也会上下使用一排和周边融合的像素来实现立体感，让用户觉得这是一个真实的滑块;Android 4.x 大量使用黑色、蓝色和浅灰色，也让整个界面看起来没有Win8扁平化那样乍眼。可以说，Android Design 在拟物和极简之间找到了一个微妙的平衡，恰到好处的同时又把机器人的Geek风格表达的淋漓尽致。

而最近，Google Play 4.0的大改版、Google Glass UI——Timeline Card的公开，都让我们看到了Google 在以Holo主题为代表的Android Design 发展方向上有着很成熟的考虑。而随着Android 4.x 设备已超过半数(Google 最新Android 4.x 比例为54.3%，上个月为45.1%)，Google play进一步被重视，Adnroid Design将逐渐成为Android应用的主流风格。到时候如果你再照搬iOS UI，那简直是在自毁形象啊!

一些遵守Android UI规范并且设计较好的作品，有国内的Fuubo，国外的Carbon、Press等等，如果不知道怎么设计的，也可以去下载他们的App来借鉴一下。

对于Android Design，国内外已经出现了很多优秀的作品。而由于国内Android 环境和国际有所脱节，Google Play对国内用户不友好，Android 4.0以下机器仍占绝大部分，导致很多Android开发者不太重视Android Design。我们希望国内的开发者能尽快重视这个问题，从Android的设计语言上来开发App。