冒泡排序与选择排序的区别分析_冒泡排序和选择排序的区别-优快云博客

本文链接：https://blog.youkuaiyun.com/coldplay19921221/article/details/107861595

冒泡排序与选择排序的区别

冒泡排序与选择排序很类似，有些初学者不注意很容易将两者混淆，因此想写一篇博客，详解两种排序算法的区别。

1. 冒泡排序

1.1 原理

冒泡排序属于一种典型的交换排序。冒泡排序的思想就是利用的比较交换，利用循环将第 i 小或者大的元素归位，归位操作利用的是对 n 个元素中相邻的两个进行比较，如果顺序正确就不交换，如果顺序错误就进行位置的交换。通过重复的循环访问数组，直到没有可以交换的元素，那么整个排序就已经完成了。

1.2 示例

通过一个示例来理解冒泡排序，假设有一个数组 a[5] = {3，4，1，5，2}；

第1轮排序

首先进行第1轮排序，黄色代表当前比较的元素，绿色代表已经归位的元素。
　　（1）比较第1个和第2个元素，4>3，交换。
　　（2）比较第2个和第3个元素，1<3，不交换。
　　（3）比较第3个和第4个元素，5>1，交换。
　　（4）比较第4个和第5个元素，2>1，交换。
　　最后，我们可以看到 1 已经位于最顶部。需要四次比较才能把五个数比较完。　
　　　在这里插入图片描述

第2轮排序

第2轮排序的初始状态是第一遍排序的最终状态，即4，3，5，2，1。
　　（1）比较第一个和第二个元素，3<4，不交换。
　　（2）比较第二个和第三个元素，5>3，交换。
　　（3）比较第三个和第四个元素，2<3，不交换。
　　第2轮排序，会让 2 归位，并且这一遍只用进行三次比较就可以了。
　　在这里插入图片描述

第3轮排序

第3轮排序的初始状态是第二遍排序的最终状态，即4，5，3，2，1。
　　（1）比较第一个和第二个元素，5>4，交换。
　　（2）比较第二个和第三个元素，3<4，不交换。
　　第3轮排序，会让 3 归位，并且这一遍只用进行两次比较就可以了。
　　然而我们可以看到这一次五个数已经全部完成了归位，但是当我们采用普通的冒泡排序的时候，算法仍然会继续向下进行。
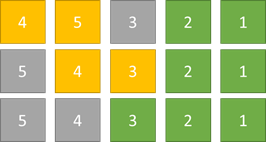
　　在这里插入图片描述

第4轮排序

第4轮排序的初始状态是第三遍排序的最终状态，即5，4，3，2，1。
　　这个时候就可以看出，排序实际上在第三遍已经完成了，但是算法还是会继续向下进行。
　　在这里插入图片描述

1.3 C++代码

void swap(int *a,int *b) 
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

void BubbleSort(int a[], int length)
{
	int i, j;
    for (i=0; i<length-1; i++)
    {
        for (j=0; j<length-1-i; j++)
        {
            if (a[j] > a[j+1])
                swap(&a[j], &a[j+1]);
        }
    }
}

2. 选择排序

2.1原理

选择排序是一种不稳定的排序算法。其原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到全部待排序的数据元素排完。

2.2 示例

通过一个示例来理解选择排序，假设有一个数组 a[5] = {3，4，1，5，2}；

第1轮排序

1）找出数组元素2到元素5中的最小值为1，对应元素3；
2）比较元素1和最小值，如果元素1>最小值，即3>1，交换元素1和元素3；
在这里插入图片描述
经过第1轮排序后，第1个位置确定下来。

第2轮排序

1）找出数组元素3到元素5中的最小值为2，对应元素5；
2）比较元素2和最小值，如果元素2>最小值，即4>2，交换元素2和元素5；
在这里插入图片描述
经过第2轮排序后，第2个位置确定下来。

第3轮排序

1）找出数组元素4到元素5中的最小值为4，对应元素5；
2）比较元素3和最小值，由于元素3<最小值，不交换；
在这里插入图片描述
经过第3轮排序后，第3个位置确定下来。

第4轮排序

1）找出最小值为4，对应元素5；
2）比较元素4和最小值，如果元素4>最小值，即5>4，交换元素4和元素5；
在这里插入图片描述
经过第4轮排序后，第4个位置确定下来，由于只剩元素5，因此第五个位置也确定下来，完成排序。

2.3 C++代码

    void SelectSort(int a[], int length)
    {
        int i,j;
        for (i = 0 ; i < length - 1 ; i++)
        {
            int min = i;
            for (j = i + 1; j < length; j++)
            {
                if (a[j] < a[min])
                    min = j;
            }
            swap(&a[min], &a[i]);
        }
    }