1.【 单选 】2 分
世界上的第一台通用计算机的名字是()。
- A.
ABC计算机
- B.
ENIAC计算机
- C.
图灵机
- D.
银河一号
A
B
C
D
2.【 单选 】2 分
一个float类型的变量在计算机中占用()个字节。
- A.
1
- B.
2
- C.
4
- D.
8
A
B
C
D
3.【 单选 】2 分
给定两个二进制数:0100 10112和1010 01012,其按位异或结果的十进制值是()。
- A.
241
- B.
240
- C.
239
- D.
238
A
B
C
D
4.【 单选 】2 分
后缀表达式a b c + * d -的前缀形式为:
- A.
- * + b c a d
- B.
– d * + c b a
- C.
(a + b) * c - d
- D.
- d + b c * a
A
B
C
D
5.【 单选 】2 分
对于一个具有n个节点、没有重边和自环的无向连通图,其边的数量不可能是():
- A.
n
- B.
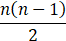
- C.
n-1
- D.
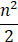
A
B
C
D
6.【 单选 】2 分
已知2023年1月1日是星期日,那么2053年1月1日是星期()。
- A.
一
- B.
二
- C.
三
- D.
四
A
B
C
D
7.【 单选 】2 分
以下哪种排序算法的时间复杂度是
![]()
:
- A.
快速排序
- B.
冒泡排序
- C.
插入排序
- D.
选择排序
A
B
C
D
8.【 单选 】2 分
设x=true, y=false, z=false。以下逻辑运算表达式值为false的是:
- A.
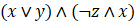
- B.
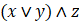
- C.
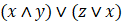
- D.
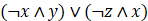
A
B
C
D
9.【 单选 】2 分
1936年,()提出了一个问题,即是否存在一种算法,可以判断任何给定的程序是否在有限步骤内停止运行。他证明了这个问题是不可解的,也就是说,无法找到一种通用的算法来解决所有程序的停机性质。
- A.
艾伦·麦席森·图灵(Alan Mathison Turing)
- B.
约翰·冯·诺依曼(John von Neumann)
- C.
罗伯特·塔扬(Robert Tarjan)
- D.
克劳德·艾尔伍德·香农(Claude Elwood Shannon)
A
B
C
D
10.【 单选 】2 分
给下图5个区域涂上4种不同颜色的任意一种,要求相邻两块区域的颜色不同,且每块区域都填上颜色。共有()种不同的涂色方案:
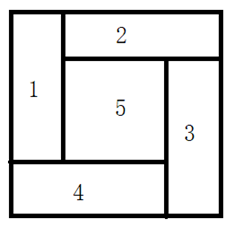
- A.
36
- B.
48
- C.
72
- D.
108
A
B
C
D
11.【 单选 】2 分
已知如果一棵二叉树只有根结点,那么这棵二叉树高度为 1。考虑一棵具有50个节点的二叉搜索树,其高度最大为():
- A.
25
- B.
6
- C.
50
- D.
49
A
B
C
D
12.【 单选 】2 分
一棵二叉树的中序遍历序列为ABCDEFG,后序遍历序列为GFEDCBA,则这棵二叉树根节点左子树中的节点数目为():
- A.
0
- B.
1
- C.
2
- D.
3
A
B
C
D
13.【 单选 】2 分
对于以下程序段:
int i = 0, s = 0;
while (s <= n) {
i++;
s = s + i;
}
该程序的时间复杂度为:
- A.
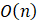
- B.
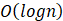
- C.
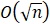
- D.
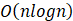
A
B
C
D
14.【 单选 】2 分
一辆卡车违反交通规则,撞人后逃跑。现场有3个目击证人,但都没有记住车号,只记下车号的某些特征。甲说: 牌照的前面2位数字是相同的; 乙说: 牌照后面2位数字是相同的,但与前面2位不同;丙是数学家,他说: 四位的车号刚好是一个整数的平方,且没有前导零。请根据以上的线索查得肇事车号为():
- A.
0000
- B.
2244
- C.
6633
- D.
7744
A
B
C
D
15.【 单选 】2 分
考虑以下将数组从小到大排序的冒泡排序算法实现:
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (a[j] > a[j + 1]) {
swap(a[j], a[j + 1]);
}
}
}
以下优化方法错误的是():
- A.
局部有序法:当a[j] < a[j + 1]且a[j] > a[j - 1](若有)时,由于该元素满足局部有序性质,无法继续上浮或者下沉,因此可以不再对其进行操作。对应的代码为:
for (int i = 0; i < n; i++) { for (int j = 0; j < n - i; j++) { if (j > 0 && a[j] < a[j + 1] && a[j] > a[j - 1]) break; if (a[j] > a[j + 1]) { swap(a[j], a[j + 1]); } } } - B.
标志位优化法:可以设置一个标志位,若某一趟遍历中没有发生元素交换,则说明序列已经有序,可以提前结束排序。对应的代码为:
for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a[j], a[j + 1]); swapped = true; } } if (!swapped) break; } - C.
双向冒泡排序:正向冒泡一次,将最大元素放到序列末尾;反向冒泡一次,将最小元素放到序列开头。通过双向遍历,可以减少排序回合数。对应的代码为:
int start = 0; int end = n - 1; while (start < end) { bool swapped = false; for (int i = start; i < end; i++) { if (a[i] > a[i + 1]) { swap(a[i], a[i + 1]); swapped = true; } } end--; for (int i = end; i > start; i--) { if (a[i] < a[i - 1]) { swap(a[i], a[i - 1]); swapped = true; } } start++; if (!swapped) break; } - D.
边界优化:每一趟排序时,记录最后一次发生交换的位置,下一趟排序只需遍历到该位置即可。这样可以缩小每一趟排序的范围,提高效率。对应的代码为:
bool isSwap = true; int lastSwapIndex = n - 1; for (int i = 0; i < n - 1; ++i) { if (!isSwap) break; isSwap = false; int end = lastSwapIndex; for (int j = 0; j < end; ++j) { if (a[j] > a[j + 1]) { swap(a[j], a[j + 1]); isSwap = true; lastSwapIndex = j; } } }
A
B
C
D
16.【 单选 】1.5 分
阅读程序(程序输入不超过数组或字符串定义的范围;判断题正确填√,错误填×;除特殊说明外,判断题1.5分,选择题3分,共计40分)
(一)
01 #include <iostream>
02 using namespace std;
03
04 unsigned int f(unsigned int x) {
05 if (x == 0) {
06 return sizeof(unsigned int) * 8;
07 }
08 unsigned int ret = 0;
09 while ((x & 1) == 0) {
10 x >>= 1;
11 ret++;
12 }
13 return ret;
14 }
15
16 unsigned int g(unsigned int x) {
17 x ^= x >> 16;
18 x ^= x >> 8;
19 x ^= x >> 4;
20 x ^= x >> 2;
21 x ^= x >> 1;
22 return x & 1;
23 }
24
25 int main()
26 {
27 int x, y;
28 cin >> x >> y;
29 cout << f(x) << " " << g(y);
30 return 0;
31 }
输入保证在32位有符号整数的范围内,完成下面的判断题和单选题。
- 判断题
当输入为25 13时,输出为0 0。()
- A.
正确
- B.
错误
A
B
17.【 单选 】1.5 分
当输入的x值为14时,f中的while循环将执行1次。()
- A.
正确
- B.
错误
A
B
18.【 单选 】2 分
(2分)当输入的两个整数的绝对值小于等于32767时,可以去掉f和g函数中所有的unsigned关键字,且运行结果不变。()
- A.
正确
- B.
错误
A
B
19.【 单选 】2 分
(2分)对于f函数,最坏情况下的时间复杂度为():
- A.
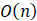
- B.
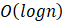
- C.
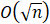
- D.
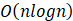
A
B
C
D
20.【 单选 】3 分
f函数的功能是():
- A.
求出一个数x的二进制表示数中的最低有效位。
- B.
求出一个数x的二进制表示数中末尾0的个数。
- C.
求出一个数x的二进制表示数中1的个数的奇偶性(偶数返回0 , 奇数返回1)。
- D.
求出一个数x的二进制表示数中1的个数。
A
B
C
D
21.【 单选 】3 分
g函数的功能是():
- A.
求出一个数x的二进制表示数中的最低有效位。
- B.
求出一个数x的二进制表示数中末尾0的个数。
- C.
求出一个数x的二进制表示数中1的个数的奇偶性(偶数返回0 , 奇数返回1)。
- D.
求出一个数x的二进制表示数中最后一个1在第几位(从后往前算)
A
B
C
D
22.【 单选 】1.5 分
(二)
01 #include <bits/stdc++.h>
02 #define int long long
03 using namespace std;
04
05 int p[5000010];
06 int cnt;
07 int vis[5000010];
08 int f[5000010], g[5000010];
09
10 inline void init(int n)
11 {
12 int i;
13 for (f[1] = g[1] = 1, i = 2; i <= n; i++)
14 {
15 if (!vis[i])
16 {
17 p[++cnt] = i;
18 f[i] = -1;
19 g[i] = i - 1;
20 }
21 for (int j = 1; i * p[j] <= n && j <= cnt; j++)
22 {
23 vis[i * p[j]] = 1;
24 if (i % p[j] == 0)
25 {
26 f[i * p[j]] = 0;
27 g[i * p[j]] = g[i] * p[j];
28 break;
29 }
30 else
31 {
32 f[i * p[j]] = -f[i];
33 g[i * p[j]] = g[i] * (p[j] - 1);
34 }
35 }
36 }
37 }
38
39 signed main()
40 {
41 init(5000000);
42
43 int x;
44 cin >> x;
45 cout << f[x] << " " << g[x] << endl;
46 return 0;
47 }
假设输入的 x 是不超过 20000 的自然数,完成下面的判断题和单选题:
- 判断题
执行完第41行后,p[20]的值是73。()
- A.
正确
- B.
错误
A
B
23.【 单选 】1.5 分
第13行中的i可以从1开始枚举,且对结果没有影响。()
- A.
正确
- B.
错误
A
B
24.【 单选 】2.5 分
(2.5分)对于任意的正整数
![]()
,满足
![]()
, 且
![]()
(gcd代表二者的最大公因数),则必然成立:
![]()
和
![]()
。 ()
- A.
正确
- B.
错误
A
B
25.【 单选 】3 分
init(int n)函数的时间复杂度为:()
- A.
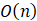
- B.
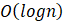
- C.
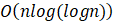
- D.
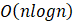
A
B
C
D
26.【 单选 】3 分
在执行完init(int n)函数后,f[1],f[2], …, f[100]中有()个等于-1:
- A.
27
- B.
28
- C.
29
- D.
30
A
B
C
D
27.【 单选 】3.5 分
(3.5分)g[12050]的值是:()
- A.
1
- B.
2400
- C.
3600
- D.
4800
A
B
C
D
28.【 单选 】1.5 分
(三)
01 #include <bits/stdc++.h>
02 using namespace std;
03
04 int n;
05 int a[100010], b[100010];
06 int mp[100010], f[100010];
07
08 int main()
09 {
10 cin >> n;
11 for (int i = 1; i <= n; i++)
12 {
13 cin >> a[i];
14 mp[a[i]] = i;
15 f[i] = 0x7fffffff;
16 }
17 for (int i = 1; i <= n; i++)
18 {
19 cin >> b[i];
20 }
21 int len = 0;
22 f[0] = 0;
23 for (int i = 1; i <= n; i++)
24 {
25 int l = 0, r = len;
26 if (mp[b[i]] > f[len])
27 {
28 f[++len] = mp[b[i]];
29 }
30 else
31 {
32 while (l < r)
33 {
34 int mid = (l + r) >> 1;
35 if (f[mid] > mp[b[i]])
36 {
37 r = mid;
38 }
39 else
40 {
41 l = mid + 1;
42 }
43 }
44 f[l] = min(f[l], mp[b[i]]);
45 }
46 }
47 cout << len;
48 return 0;
49 }
判断题
当输入为5 1 1 1 1 1 2 2 2 2 2时,第28行将从未被执行过。()
- A.
正确
- B.
错误
A
B
29.【 单选 】1.5 分
当输入为7 1 2 3 4 5 7 6 2 3 4 6 8 6 4时,输出结果为4。()
- A.
正确
- B.
错误
A
B
30.【 单选 】1.5 分
将第37行改为r = mid - 1; ,不会对程序的正确性造成影响。()
- A.
正确
- B.
错误
A
B
31.【 单选 】2 分
(2分)该程序的时间复杂度为:()
- A.
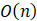
- B.
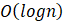
- C.
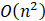
- D.
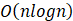
A
B
C
D
32.【 单选 】2.5 分
(2.5分)当输入第一行为100,第二行跟100个1,第三行跟100个1时,输出为:()
- A.
1
- B.
0
- C.
100
- D.
50
A
B
C
D
33.【 单选 】3 分
当输入为10 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1时,第34行将执行()次:
- A.
8
- B.
9
- C.
10
- D.
11
A
B
C
D
34.【 单选 】3 分
完善程序(单选题,每小题3分,共计30分)
(1)(求先序排列)给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 ≤ 8)。
试补全程序。
01 #include <bits/stdc++.h>
02 using namespace std;
03
04 void dfs(string m, string e)
05 {
06 ①
07 {
08 char c = e[②];
09 cout << ③;
10 int k = m.find(c);
11 dfs(④, e.substr(0, k));
12 dfs(m.substr(k+1, m.length()-1-k), ⑤);
13 }
14 }
15
16 int main()
17 {
18 string mid_s, end_s;
19 cin >> mid_s >> end_s;
20 dfs(mid_s, end_s);
21 return 0;
22 }
①处应填( )
- A.
if (m.length() > 0)
- B.
if (m.length() > e.length())
- C.
if (e.length() > m.length())
- D.
if (e.length() – 1 > 0)
A
B
C
D
35.【 单选 】3 分
②处应填( )
- A.
m.length()
- B.
e.length()
- C.
0
- D.
- e.length() – 1
A
B
C
D
36.【 单选 】3 分
③处应填( )
- A.
c
- B.
m[0]
- C.
e[0]
- D.
m[m.length()]
A
B
C
D
37.【 单选 】3 分
④处应填( )
- A.
m.substr(0, k - 1)
- B.
m.substr(0, m.length() - 1)
- C.
m.substr(0, k)
- D.
m
A
B
C
D
38.【 单选 】3 分
⑤处应填( )
- A.
e.substr(k, e.length() - 1)
- B.
e.substr(k, e.length() - 1 - k)
- C.
e.substr(k + 1, e.length() - 1)
- D.
e.substr(k + 1, e.length() – 1 - k)
A
B
C
D
39.【 单选 】3 分
(2)(最大正方形)在一个 n×m的只包含 0 和 1 的矩阵里找出一个不包含 0 的最大正方形,输出边长。
输入第一行为两个整数
![]()
,接下来 n 行,每行 m 个数字,用空格隔开,为 0 或 1。
例如,对于:
4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1
来说,最大正方形的边长为2。
提示:对于这个题,由于数据范围不大,可考虑二维前缀和直接解决。
试补全程序。
01 #include <bits/stdc++.h>
02 using namespace std;
03
04 int ma[101][101];
05 int sum[101][101];
06
07 int main()
08 {
09 int n, m;
10 int rst = 0;
11 cin >> n >> m;
12 for (int i = 1; i<=n; i++)
13 for (int j = 1; j<=m; j++)
14 cin >> ma[i][j];
15 for (int i = 1; i<=n; i++)
16 for (int j = 1; j<=m; j++)
17 {
18 sum[i][j] = ①;
19 }
20 for (int i = 1; i<=n; i++)
21 for (int j = 1; j<=m; j++)
22 for (int k = 1; k<=②; k++)
23 {
24 int r = ③;
25 if (r == ④)
26 rst = ⑤;
27 }
28 cout << rst;
29 return 0;
30 }
①处应填( )
- A.
ma[i][j];
- B.
sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + sum[i][j];
- C.
sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + ma[i][j];
- D.
sum[i-1][j] + sum[i][j-1] + sum[i][j];
A
B
C
D
40.【 单选 】3 分
②处应填( )
- A.
n*m
- B.
max(n, m)
- C.
min(n-i+1, m-j+1)
- D.
max(n-i+1, m-j+1)
A
B
C
D
41.【 单选 】3 分
③处应填( )
- A.
k * k
- B.
k
- C.
sum[i+k-1][j+k-1] - sum[i-1][j+k-1] - sum[i+k-1][j-1] + ma[i-1][j-1];
- D.
sum[i+k-1][j+k-1] - sum[i-1][j+k-1] - sum[i+k-1][j-1] + sum[i-1][j-1];
A
B
C
D
42.【 单选 】3 分
④处应填( )
- A.
k
- B.
k*k
- C.
n*m
- D.
sum[i+k-1][j+k-1] - sum[i-1][j+k-1] - sum[i+k-1][j-1] + sum[i-1][j-1]
A
B
C
D
43.【 单选 】3 分
⑤处应填( )
- A.
k
- B.
rst
- C.
r > (rst*rst) ? k : rst;
- D.
r < (rst*rst) ? k : rst;
A
B
C
D




















 1454
1454

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








