以为是高性能神仙算法，一看源代码才发现...

点击上方“编程派”，选择设为“设为星标”

优质文章，第一时间送达！

在昨天的文章中，我们讲到了 RSA 算法。RSA 算法的根本原理中，有两个核心质数 p和 q，他们相乘得到一个数 n。由于反向从 n 分解出 p 和 q 非常困难，所以只要 p 和 q 足够大，RSA 算法在现在的计算机水平下就无法被破解。

现在，你先暂停一下，打开百度或者 Google，搜索一下 RSA 算法的教程。随便看10篇。

你会发现，这些教程无一例外都是说：寻找两个足够大的质数 p 和 q。但他们都不会告诉你，怎么寻找。

在现在的数学体系中，质数是找出来的，而不是生成出来的。还没有一个完美的通项公式可以生成质数。我们可以做到快速检查一个数是不是质数，但是我们现在还做不到直接生成一个质数。

那么问题来了，RSA 算法中生成密钥时，需要的这两个质数，到底是怎么来的？

当我们使用 RSA 算法生成2048 bit的密钥时，我们需要找到的两个质数 p 和 q，他们各是1024bit。1024bit的数字有多大？它最小的值为  ，最大为  。如果你从最小的这个数字开始数，数到最大的这个数，每秒你能数1亿个数字，你需要数570044753571256946895391042233962688235025678254156066950247593726955466151385601004275993538836681954338260654082297557264046704764131857219835840434659197037569423594829671728507799344387665269701556798848952843855120124119935570376436804099528276139492994306780499238797710357939232321万年才能数完。

这么大范围的数字里面，让你去找两个质数。你说，这 TM 怎么找？

所以，Python的这个 rsa 库，里面是使用了什么神仙算法，能够快速找到这两个质数的？于是我去阅读了它的源代码^[1]。结果吓得我一身冷汗。

生成密钥使用的是rsa.newkeys()函数，于是我首先在 rsa/key.py文件中找到了这个函数：

先看758-762行，这里它通过poolsize参数来决定使用CPU的几个核，如果我的 CPU 是4核心，那么可以同时开4个进程来寻找质数。但这段代码我们可以先跳过，因为在昨天的文章里面，我们没有指定 poolsize参数，所以它使用默认值1.于是代码运行到第767行，通过gen_keys函数来生成p 和 q。

我们再来看gen_keys函数：

可以看到，在第714行，通过函数find_p_q生成了 p 和 q，并且这里如果我们的密钥是2048bit的话，p 和q 均是1024bit。

我们再来看 find_p_q函数：

这个函数很长，但是大部分是在验证生成的 p 和 q 是否符合要求（不能相等，并且要相差足够大），如果不符合要求就重试。所以真正核心的代码只有第613行和第615行。这里调用的genprime_func函数是通过参数传进来的。而这个genprime_func是我们在newkeys函数第764行获得的rsa.prime.getprime函数。

现在我们进入/rsa/prime.py文件，阅读getprime函数的源代码：

这段代码竟然非常简单。在第162行先判断要生成的质数的bit 数不小于3.然后高潮来了：

while True:
        integer = rsa.randnum.read_random_odd_int(nbits)

        # Test for primeness
        if is_prime(integer):
            return integer

开一个死循环，调用read_random_odd_int不停获取nbit的奇数，然后，使用is_prime判断它是不是质数，如果是，返回这个数。如果不是质数，继续随机生成一个 nbit 的奇数，再判断它是不是质数。

这 TM 在逗我？在死循环里面随机生成奇数，然后判断是不是质数，不是就重试直到随机到一个质数为止？

在  到  这么大的范围里面随机选奇数？这要选多少年才碰得上两个质数啊？

为了解决这个疑惑，我们来看一下素数定理^[2]。



对于正实数  ，定义π(x)为素数计数函数，亦即不大于x的素数个数。数学家找到了一些函数来估计π(x)的增长：

”

在  足够大时，可以使用这个公式估算出不大于  的质数的个数。

那么我们来看看，在  到  的范围中，质数的密度是多少：

质数的密度竟然高达0.14%！那么随机选一个数字，不是质数的概率是99.86%。我们来计算一下，如果随机选10000个数字，即使在不考虑奇偶性的情况下：

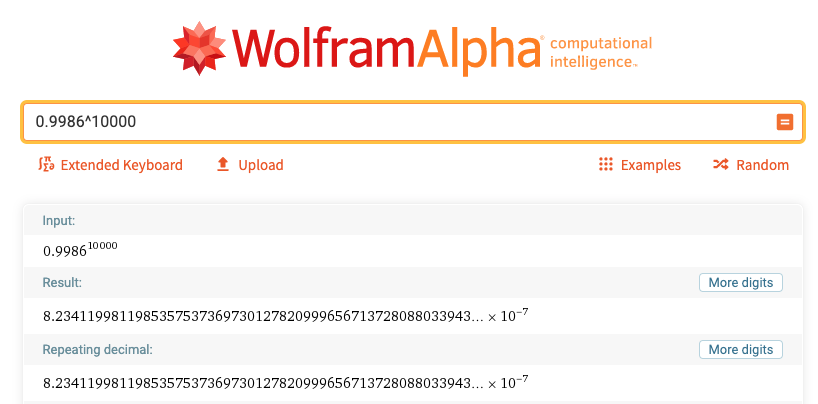
也就是说，在随机10000个数字里面，不出现质数的概率是一千万分之一。出现质数的概率超过99.9999%

而用 Python 循环10000次，并不需要多长时间。所以，rsa 库里面的这个算法，竟然没什么问题！！

最后，大家有兴趣可以看看prime.py中的is_prime函数，用于快速判断一个数是不是质数。还有randnum.py中的read_random_odd_int用于随机生成一个奇数，代码都很简单，相信你能学到不少东西。

参考资料

[1]

源代码: https://github.com/sybrenstuvel/python-rsa

[2]

素数定理: https://zh.wikipedia.org/wiki/%E8%B3%AA%E6%95%B8%E5%AE%9A%E7%90%86

回复下方「关键词」，获取优质资源

回复关键词「 pybook03」，立即获取主页君与小伙伴一起翻译的《Think Python 2e》电子版
回复关键词「入门资料」，立即获取主页君整理的 10 本 Python 入门书的电子版
回复关键词「m」，立即获取Python精选优质文章合集
回复关键词「book 数字」，将数字替换成 0 及以上数字，有惊喜好礼哦~
题图：pexels，CC0 授权。

好文章，我在看