Covering HDU - 6185 （找递推公式+矩阵快速幂）

Covering

HDU - 6185

Bob's school has a big playground, boys and girls always play games here after school.

To protect boys and girls from getting hurt when playing happily on the playground, rich boy Bob decided to cover the playground using his carpets.

Meanwhile, Bob is a mean boy, so he acquired that his carpets can not overlap one cell twice or more.

He has infinite carpets with sizes of 1×2 and 2×1, and the size of the playground is 4×n

.

Can you tell Bob the total number of schemes where the carpets can cover the playground completely without overlapping?

Input There are no more than 5000 test cases.

Each test case only contains one positive integer n in a line.

1≤n≤1018
Output For each test cases, output the answer mod 1000000007 in a line.
Sample Input

1
2

Sample Output

1
5

摘自博客点击打开链接

首先可以通过dfs打表找规律

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
bool book[7][1007];
int cnt;
int n;
bool findpos(int &x,int &y){
    for(int i = 1; i <= 4; i++){
        for(int j = 1; j <= n; j++){
            if(!book[i][j]){
                x = i,y = j;
                return false;
            }
        }
    }
    return true;
}
void dfs(int x,int y){
    if(!book[x+1][y] && x < 4){
        book[x][y] = book[x+1][y] = true;
        int newx,newy;
        if(findpos(newx,newy)){
            book[x][y] = book[x+1][y] = false;
            cnt++;
            return;
        }
        dfs(newx,newy);
        book[x][y] = book[x+1][y] = false;
    }
    if(!book[x][y+1] && y < n){
        book[x][y] = book[x][y+1] = true;
        int newx,newy;
        if(findpos(newx,newy)){
            book[x][y] = book[x][y+1] = false;
            cnt++;
            return;
        }
        dfs(newx,newy);
        book[x][y] = book[x][y+1] = false;
    }
}
int main(){
    while(cin >> n){
        cnt = 0;
        memset(book,false,sizeof(book));
        dfs(1,1);
        cout << cnt << endl;
    }
    return 0;
}

得到了答案：1 ，5 ，11 ，36 ，95 ，281，781，2245，6336，18061

然后觉得有一个边长是常数4，就写了五层for循环确定ans[i]与前四项和一个常数之间的系数关系，得到：

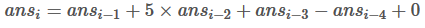
（这个递推式我没想明白为什么会和前四项有关，可能是试出来的？）

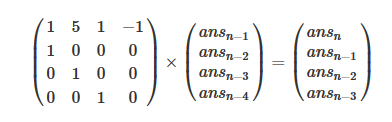
，然后想到矩阵快速幂，容易得到：

  需要注意的一点是，因为有一个系数是−1

，所以在矩阵乘法的过程中，在两两相加的时候要再加上一个mod之后再取模，不然的话有可能出现一个小的正数加上一个大的负数的情况。

然后因为需要前四项，所有可以从第五项开始算，前四项直接输出，但是博客中构造了一个神奇的矩阵

1

0

1

1

这个列向量，可以直接从第一项开始算

code：

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn = 4;
const int mod = 1e9+7;
ll n;
struct Matrix{
    ll m[maxn][maxn];
    Matrix(ll i = 0){
        memset(m,0,sizeof(m));
        if(i == 1)
            for(int j = 0; j < 4; j++)
                m[j][j] = 1;
    }
    Matrix operator * (const Matrix tmp)const{
        Matrix ret;
        ll x;
        for(int i = 0; i < 4; i++){
            for(int j = 0; j < 4; j++){
                x = 0;
                for(int k = 0; k < 4; k++){
                    x += (m[i][k] * tmp.m[k][j] + mod) % mod;
                }
                ret.m[i][j] = x % mod;
            }
        }
        return ret;
    }
    Matrix q_pow(ll n){
        Matrix ret = 1,tmp = *this;
        while(n){
            if(n & 1)
                ret = ret * tmp;
            tmp = tmp * tmp;
            n >>= 1;
        }
        return ret;
    }
};
int main(){
    Matrix base1 = 0,base2 = 0;
    base1.m[0][0] = base1.m[0][2] = base1.m[1][0] = base1.m[2][1] = base1.m[3][2] = 1;
    base1.m[0][3] = -1,base1.m[0][1] = 5;
    base2.m[0][0] = 1;
    base2.m[1][0] = 0;
    base2.m[2][0] = 1;
    base2.m[3][0] = 1;
    while(~scanf("%lld",&n)){
        Matrix ans = base1.q_pow(n)*base2;
        printf("%lld\n",ans.m[0][0]);
    }
    return 0;
}