DFS算法-深度优先搜索

        最近遇到了几个DFS的题，就想着花时间把DFS算法学习一下。

        DFS算法主要通过递归的方法，以深度为优先遍历搜索类似树或图的节点。常常与回溯联系在一起，当遍历到子叶节点时，将指针回溯到没有访问过的节点，然后继续深度搜索。

        DFS算法属于基础的暴力搜索算法，在此基础上可以通过动态规划和剪枝来优化算法。

 下面通过列举两个经典的题目，来学习dfs算法。

 1.全排列问题

力扣链接：https://leetcode.cn/problems/permutations/

 此题属于一个排列组合问题，可以把搜索过程看成一个树形结构，然后进行dfs和回溯，得到所有的排列。

 

 

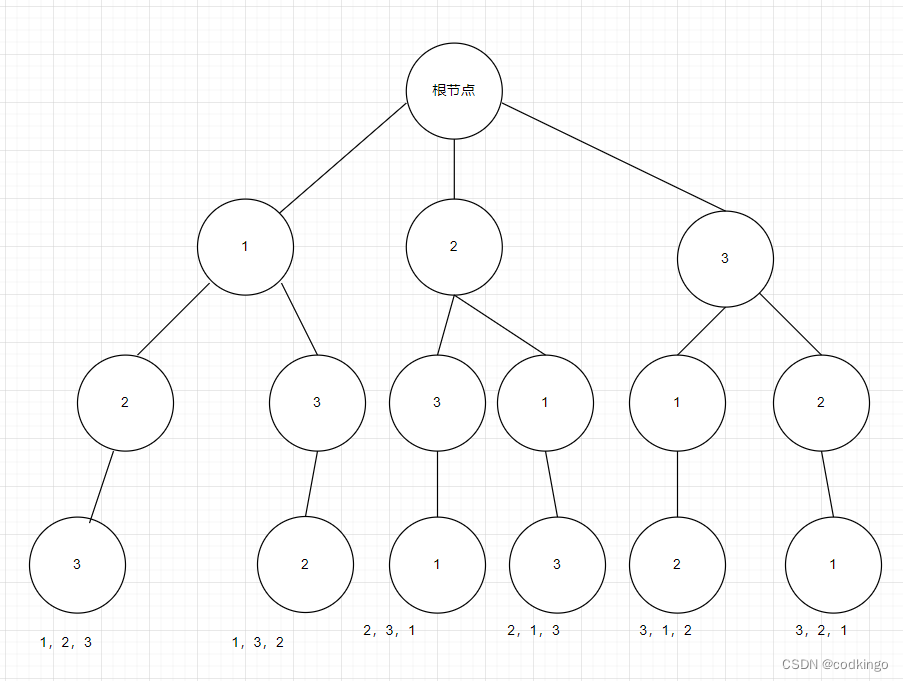
import java.util.Arrays;
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        dfs(new int[]{1,2,3},new Stack<>());
    }
    public static void dfs(int[] array,Stack<Integer> stack){
        //如果到子叶节点，则输出栈种内容
        if(array.length<=0){
            System.out.println(stack);
        }else{
            //对树的第一层节点进行遍历
            for (int i = 0 ;i < array.length; i++) {
                //用tempArray数组临时存储未访问的节点
                int[] tempArray =new int[array.length-1];
                //讲未访问的节点放入tempArray数组
                System.arraycopy(array,0,tempArray,0,i);
                System.arraycopy(array,i+1,tempArray,i,array.length-i-1);
                //将已访问的节点压入栈中
                stack.push(array[i]);
                //递归深度搜索
                dfs(tempArray,stack);
                //当访问到子叶节点，开始回溯
                stack.pop();
            }
        }
    }
}

通过递归来优先深度搜索树，其次通过for循环来广度搜索树，当搜索到叶子节点时，便将搜索的结束进行输出。 用临时数组tempArray来存储未访问过的节点，将以访问的节点压入栈中，当访问到叶子节点时，tempArray长度为0，便输出栈。每访问一个节点，入栈，每退回一个节点，出栈。

 2.水往低处流

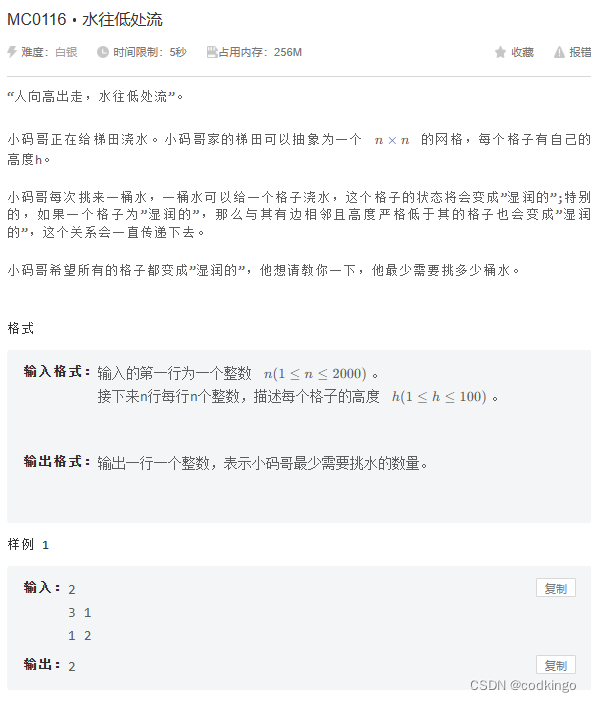
 一个典型的dfs题目，只要被访问的元素的高度大于四周元素的高度则深度搜索，直到四周元素的高度都大于被访问元素，或者到达矩阵边界，则停止搜索。

 

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    public static int[][] pos = new int[2001][2001];
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n=sc.nextInt();
        int[][] hs=new int[n+1][n+1];
        TianDi[] tianDis= new TianDi[n*n];

        int count=0;

        for (int i = 1; i < n+1; i++) {
            for (int j = 1; j < n+1; j++) {
                hs[i][j]=sc.nextInt();
                tianDis[count]=new TianDi(i,j,hs[i][j]);
                count++;
            }
        }

        //排序
        Arrays.sort(tianDis,(o1,o2)->o2.h-o1.h);

        int ans=0;

        for (int i = 0; i < count; i++) {
            if(pos[tianDis[i].x][tianDis[i].y]==1) continue;
            ans++;
            dfs(hs,tianDis[i].x,tianDis[i].y,tianDis[i].h);
        }
        System.out.println(ans);

    }

    public static void dfs(int[][] hs,int x,int y,int h){
        pos[x][y] =1;
        if(x+1<= hs.length-1&& h > hs[x+1][y]&&pos[x+1][y] == 0) dfs( hs, x+1, y,  hs[x+1][y]);
        if(x-1>=1 && h> hs[x-1][y]&&pos[x-1][y] == 0) dfs( hs, x-1, y,  hs[x-1][y]);
        if(y+1<=  hs.length-1&&h> hs[x][y+1]&&pos[x][y+1]==0) dfs( hs, x, y+1,  hs[x][y+1]);
        if(y-1>= 1&& h> hs[x][y-1]&&pos[x][y-1] == 0) dfs( hs, x, y-1,  hs[x][y-1]);
    }
}
class TianDi{
    int x;
    int y;
    int h;

    public TianDi(int x, int y, int h) {
        this.x = x;
        this.y = y;
        this.h = h;
    }
}