机器学习函数python代码实现

最新推荐文章于 2022-12-02 11:03:48 发布

原创最新推荐文章于 2022-12-02 11:03:48 发布 · 182 阅读

0 ·

CC 4.0 BY-SA版权

python 专栏收录该内容

40 篇文章

订阅专栏

本文探讨了逻辑回归中激活函数g(z)的实现，通过Sigmoid函数将任意实数映射到0和1之间，适用于二分类问题。并介绍了成本函数的计算，通过平均损失评估模型预测与实际目标之间的差距。

激活函数逻辑回归g(z)

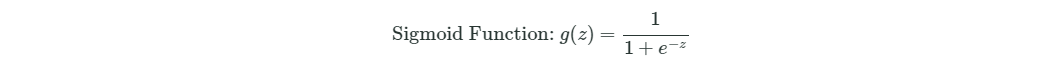
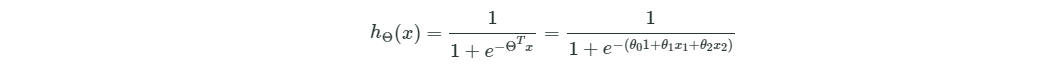
在这里插入图片描述

# The first observation
x0 = X[0]

# 随机初始化一个系数列向量
theta_init = np.random.normal(0,0.01,size=(5,1))
def sigmoid_activation(x, theta):
    x = np.asarray(x)
    theta = np.asarray(theta)
    return 1 / (1 + np.exp(-np.dot(theta.T, x)))

a1 = sigmoid_activation(x0, theta_init)
print(a1)
'''
[ 0.47681073]
'''

Cost Function

# First observation's features and target
x0 = X[0]
y0 = y[0]

theta_init = np.random.normal(0,0.01,size=(5,1))
def singlecost(X, y, theta):
    # Compute activation
    h = sigmoid_activation(X.T, theta)
    # Take the negative average of target*log(activation) + (1-target) * log(1-activation)
    cost = -np.mean(y * np.log(h) + (1-y) * np.log(1-h))
    return cost

first_cost = singlecost(x0, y0, theta_init)
'''
0.64781198784027283
'''