考研数据结构之队列（3.3）——练习题之设以数组Q.elems[maxSize]存储循环队列的元素，同时以Q.rear和Q.length分别指示循环队列中的队尾位置和队列中所含元素的个数（C表示）

题目

设以数组Q.elems[maxSize]存储循环队列的元素，同时以Q.rear和Q.length分别指示循环队列中的队尾位置和队列中所含元素的个数。试着给出该循环队列的队空条件和队满条件，并写出相应的入队（enQueue）和出队（deQueue）的操作。

分析

本题和普通的循环队列是不一样的，普通的循环队列是有两个指针的，即队头指针front和队尾指针rear，而本题中没有队头指针，因此出队的时候就需要根据已有的数据计算队头指针，来达到出队的目的。

• 队空的条件是：Q.length==0
• 队满的条件是：Q.length==maxSize

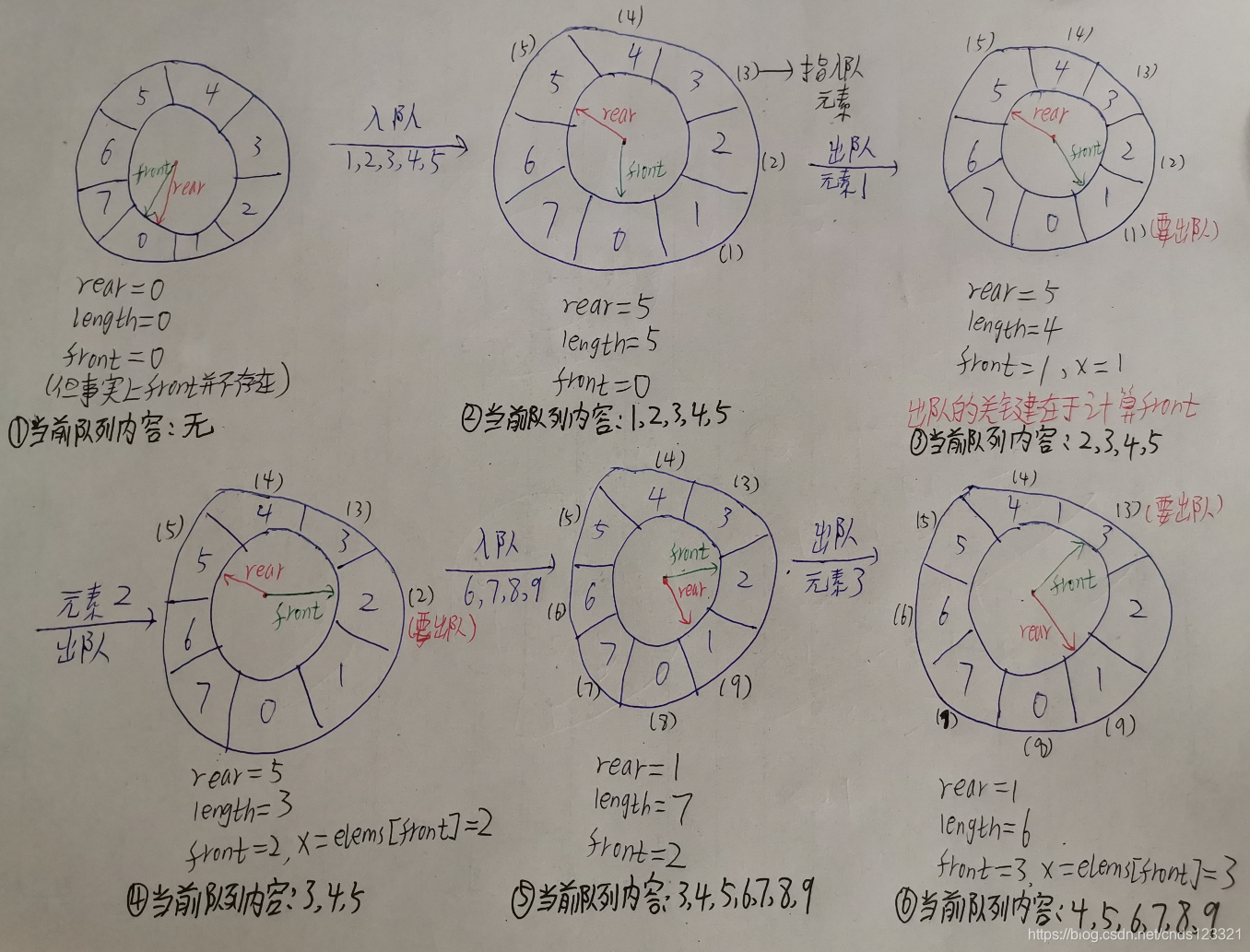
入队很简单，同普通的循环队列入队是一样的，需要注意的是注意Q.length的变化。

Q.rear=(Q.rear+1)%maxSize;// 移动指针
Q.elems[Q.rear]=x;// 入队元素
Q.length++;// 队列长度加1

出队是有些麻烦，因为没有队头指针，所以需要根据已有的信息计算队头指针，其核心语句如下：

x=Q.elems[(Q.rear-Q.length+1+maxSize)%maxSize];// 计算front的关键代码 
Q.length--;// 出队后，队列长度减1 

而(Q.rear-Q.length+1+maxSize)%maxSize就是头指针，在循环队列中的下标。

代码

核心代码如下：

/* 入队 */
int enQueue(Queue &Q,int x) {
	/* 入队元素之前判断队列是否满队 */
	if(isQueueFull(Q)==1) {
		return 0;
	} else {
		Q.rear=(Q.rear+1)%maxSize;// 移动指针
		Q.elems[Q.rear]=x;// 入队元素
		Q.length++;// 队列长度加1
		return 1;
	}
}

/* 出队 */ 
int deQueue_2(Queue &Q,int &x){
	if(Q.length==0){
		return 0;
	}
//	--(Q.length);// 参考代码是先减长度 
	x=Q.elems[(Q.rear-Q.length+1+maxSize)%maxSize];// 计算front的关键代码 
	Q.length--;// 出队后，队列长度减1 
	return 1;
}

完整代码：

#include<stdio.h>
#include<stdlib.h>

#define maxSize 8

typedef struct Queue {
	int elems[maxSize];
	int rear;// 循环队列的队尾位置
	int length;// 循环队列中所含元素的个数
} Queue;

/* 初始化队列 */
void initQueue(Queue &Q) {
	Q.rear=0;
	Q.length=0;
}

/* 判断是否循环队列队满，满队返回1，否则返回0 */
int isQueueFull(Queue Q) {
	if(Q.length==maxSize) { // 队满的条件是队列中元素个数等于maxSize
		return 1;
	}
	return 0;
}

/* 判断是否循环队列队空，空队返回1，否则返回0 */
int isQueueEmpty(Queue Q) {
	if(Q.length==0) { // 队空的条件是队列的元素个数为0
		return 1;
	}
	return 0;
}

/* 入队 */
int enQueue(Queue &Q,int x) {
	/* 入队元素之前判断队列是否满队 */
	if(isQueueFull(Q)==1) {
		return 0;
	} else {
		Q.rear=(Q.rear+1)%maxSize;// 移动指针
		Q.elems[Q.rear]=x;// 入队元素
		Q.length++;// 队列长度加1
		return 1;
	}
}

/* 出队 */ 
int deQueue_2(Queue &Q,int &x){
	if(Q.length==0){
		return 0;
	}
//	--(Q.length);// 参考代码是先减长度 
	x=Q.elems[(Q.rear-Q.length+1+maxSize)%maxSize];// 计算front的关键代码 
	Q.length--;// 出队后，队列长度减1 
	return 1;
}

/* 打印循环队列 */ 
void print(Queue Q){
	printf("打印循环队列如下：");
	while(Q.length!=0){
		printf("%d\t",Q.elems[(Q.rear-Q.length+1+maxSize)%maxSize]);
		Q.length--;
	}
	printf("\n");
}

int main(){
	Queue Q;
	initQueue(Q);// 初始化队列
	
	/* 入队 */
	enQueue(Q,1); 
	enQueue(Q,2); 
	enQueue(Q,3); 
	enQueue(Q,4); 
	enQueue(Q,5); 
	printf("\n");
	printf("入队元素：1,2,3,4,5\n");
	printf("循环队列的长度：%d\n",Q.length);
	printf("循环队列的队尾rear：%d\n",Q.rear);
	print(Q);
	
	/* 出队元素1 */
	int x;
	printf("\n");
	deQueue_2(Q,x);
	printf("出队元素：%d\n",x);
	printf("循环队列的长度：%d\n",Q.length);
	printf("循环队列的队尾rear：%d\n",Q.rear);
	print(Q);
	/* 出队元素2 */
	printf("\n");
	deQueue_2(Q,x);
	printf("出队元素：%d\n",x);
	printf("循环队列的长度：%d\n",Q.length);
	printf("循环队列的队尾rear：%d\n",Q.rear);
	print(Q); 
	
	
	/* 再入队 */ 
	enQueue(Q,6);
	enQueue(Q,7);
	enQueue(Q,8);
	enQueue(Q,9);
	printf("\n");
	printf("入队元素：6,7,8,9\n");
	printf("循环队列的长度：%d\n",Q.length);
	printf("循环队列的队尾rear：%d\n",Q.rear);
	print(Q);
	
	/* 再出队 */
	deQueue_2(Q,x);
	printf("\n");
	printf("出队元素：%d\n",x); 
	printf("循环队列的长度：%d\n",Q.length);
	printf("循环队列的队尾rear：%d\n",Q.rear);
	print(Q);
	 
	return 0;
}

运行结果如下：