激光谐振腔衍射仿真（spyder python3.11）

• 仿真方法

使用软件说明：anaconda中的spyder（python3.11）

import numpy as np
import matplotlib.pyplot as plt

# 定义参数
lamda = 0.6*10**(-3)  # 波长
n = 800  # 网格点数
L = 800 # 腔长
R = L/2  # 曲率半径
d = 10  # 衍射面尺寸
k = 2 * np.pi / lamda

# 创建坐标网格
x = np.linspace(-d/2, d/2, n)
y = np.linspace(-d/2, d/2, n)
X, Y = np.meshgrid(x, y)

M=np.zeros((800,800),dtype=float)
#接收衍射场的范围
M[300:499,300:499]=1
#镜面孔径作用

#傅里叶变换，模拟衍射过程
#初始化相位因子
slens=1/(R)*((-1/2)*((X)**2+(Y)**2))*k
confocal=np.exp(1j*slens)
fp=1
#赋值exp(jkL)/(jL)
F0=np.exp(1j*k*L)/(1j*lamda*L)
#赋值exp[jk(X^2+Y^2)/2L]
F1=np.exp(1j*k*(X**2+Y**2)/2/L)
fF1=np.fft.fft2(F1)
a=M*np.exp(-(X**2 + Y**2) / (2*R**2))#输入光场分布



for i in range(5):  
    fa=np.fft.fft2(a)
    Fuf=fa*fF1
    U=F0*np.fft.fftshift(np.fft.ifft2(Fuf))
    maxnorm=np.max(abs(U))
    U=U/maxnorm
    a=M*U*fp
    I=abs(U)**2

    plt.figure(figsize=(6, 4))  
    plt.imshow(I, cmap='gray', extent=[-1, 1, -1, 1])  
    plt.colorbar(label='Intensity')  
    plt.title(f'Diffraction Step {i+1}')  
    plt.savefig(f'diffraction_step_{i+1}.png')  
    plt.show()  
 
#假设50次之后光场变化较稳定，模拟间隔20次的衍射图案变化    
total_intensities = []
for i in range(0, 1001, 20):  
    for _ in range(20):  
      fa=np.fft.fft2(a)
      Fuf=fa*fF1
      U=F0*np.fft.fftshift(np.fft.ifft2(Fuf))
      maxnorm=np.max(abs(U))
      U=U/maxnorm
      a=M*U*fp
      I=abs(U)**2   
      plt.figure(figsize=(6, 4))  
      plt.imshow(I, cmap='gray', extent=[-1, 1, -1, 1])  
      plt.colorbar(label='Intensity')  #增加一个光强的色条
      plt.title(f'Diffraction Step {i} (after every 20 steps)')  
      plt.savefig(f'diffraction_step_{i}_every_20.png')  
      plt.show()  # 如果不想每次都显示，可以注释掉这行代码  
      
      total_intensity = np.sum(I)  # 计算当前I的总值  
      total_intensities.append(total_intensity)  # 将总值添加到列表中 

element_count = len(total_intensities) 

plt.plot(range(element_count), total_intensities)  
plt.xlabel('Iteration')  
plt.ylabel('Total Intensity')  
plt.title('Total Intensity vs Iteration')  
plt.show()
#记录总光强随循环次数的变化

1.根据菲涅尔衍射的傅里叶变换公式写出光场函数

#傅里叶变换，模拟衍射过程

#初始化相位因子

slens=1/(R)*((-1/2)*((X)**2+(Y)**2))*k

confocal=np.exp(1j*slens)

fp=1

#赋值exp(jkL)/(jL)

F0=np.exp(1j*k*L)/(1j*lamda*L)

#赋值exp[jk(X^2+Y^2)/2L]

F1=np.exp(1j*k*(X**2+Y**2)/2/L)

fF1=np.fft.fft2(F1)

a=M*np.exp(-(X**2 + Y**2) / (2*R**2))

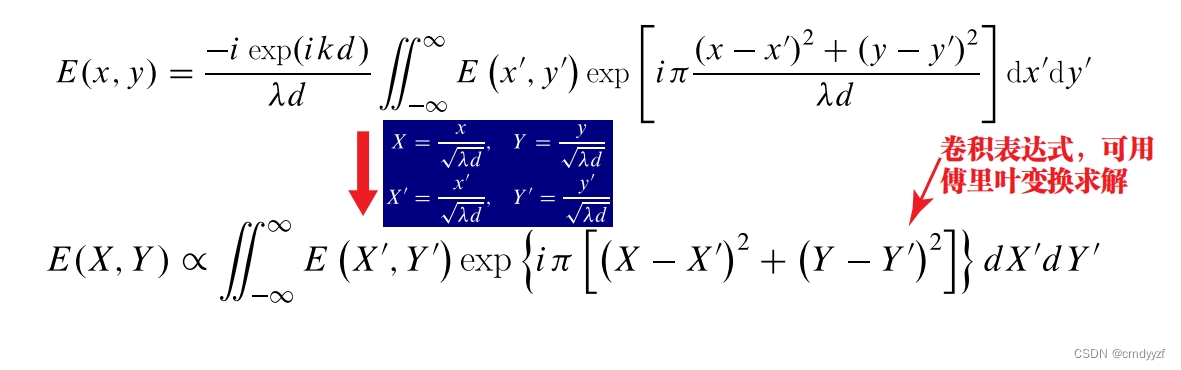
2.显示衍射图案

# 可视化衍射图案

plt.imshow(I, cmap='gray')

plt.title('Diffraction Pattern')

plt.xlabel('X')

plt.ylabel('Y')

plt.show()

3.分次数分间隔迭代显示并保存图片

for i in range(5): 

    fa=np.fft.fft2(a)

    Fuf=fa*fF1

    U=F0*np.fft.fftshift(np.fft.ifft2(Fuf))

    maxnorm=np.max(abs(U))

    U=U/maxnorm

    a=M*U*fp

    I=abs(U)**2

    plt.figure(figsize=(6, 4)) 

    plt.imshow(I, cmap='gray', extent=[-1, 1, -1, 1]) 

    plt.colorbar(label='Intensity')    #增加一个光强的色条

    plt.title(f'Diffraction Step {i+1}') 

    plt.savefig(f'diffraction_step_{i+1}.png') 

    plt.show() 

#假设50次之后光场变化较稳定，模拟间隔20次的衍射图案变化   

N=50

for i in range(N, 1001, 20): 

    for _ in range(20): 

      fa=np.fft.fft2(a)

      Fuf=fa*fF1

      U=F0*np.fft.fftshift(np.fft.ifft2(Fuf))

      maxnorm=np.max(abs(U))

      U=U/maxnorm

      a=M*U*fp

      I=abs(U)**2  

      plt.figure(figsize=(6, 4)) 

      plt.imshow(I, cmap='gray', extent=[-1, 1, -1, 1]) 

      plt.colorbar(label='Intensity')  #增加一个光强的色条

      plt.title(f'Diffraction Step {i} (after every 20 steps)') 

      plt.savefig(f'diffraction_step_{i}_every_20.png') 

      plt.show() 

• 过程分析

1.输入光场分布

a=M*np.exp(-(X**2 + Y**2) / (2*R**2))

每次循环根据新的U值改变a的取值

for i in range(1000):

    fa=np.fft.fft2(a)（将光场变换到频域）

    Fuf=fa*fF1（频域相乘）

    U=F0*np.fft.fftshift(np.fft.ifft2(Fuf))（解算新的光场）

    maxnorm=np.max(abs(U))

    U=U/maxnorm（归一化防止溢出）

a=M*U*fp（经过镜面孔径作用后新的光场分布函数）

2.记录总光强随循环次数的变化

      total_intensity = np.sum(I)  # 计算当前I的总值 

      total_intensities.append(total_intensity)  # 将总值添加到列表中 （添加进循环）

element_count = len(total_intensities)

plt.plot(range(element_count), total_intensities)  plt.xlabel('Iteration') 

plt.ylabel('Total Intensity') 

plt.title('Total Intensity vs Iteration') 

plt.show()

#记录总光强随循环次数的变化

• 结果讨论

1. 刚开始若干单程衍射

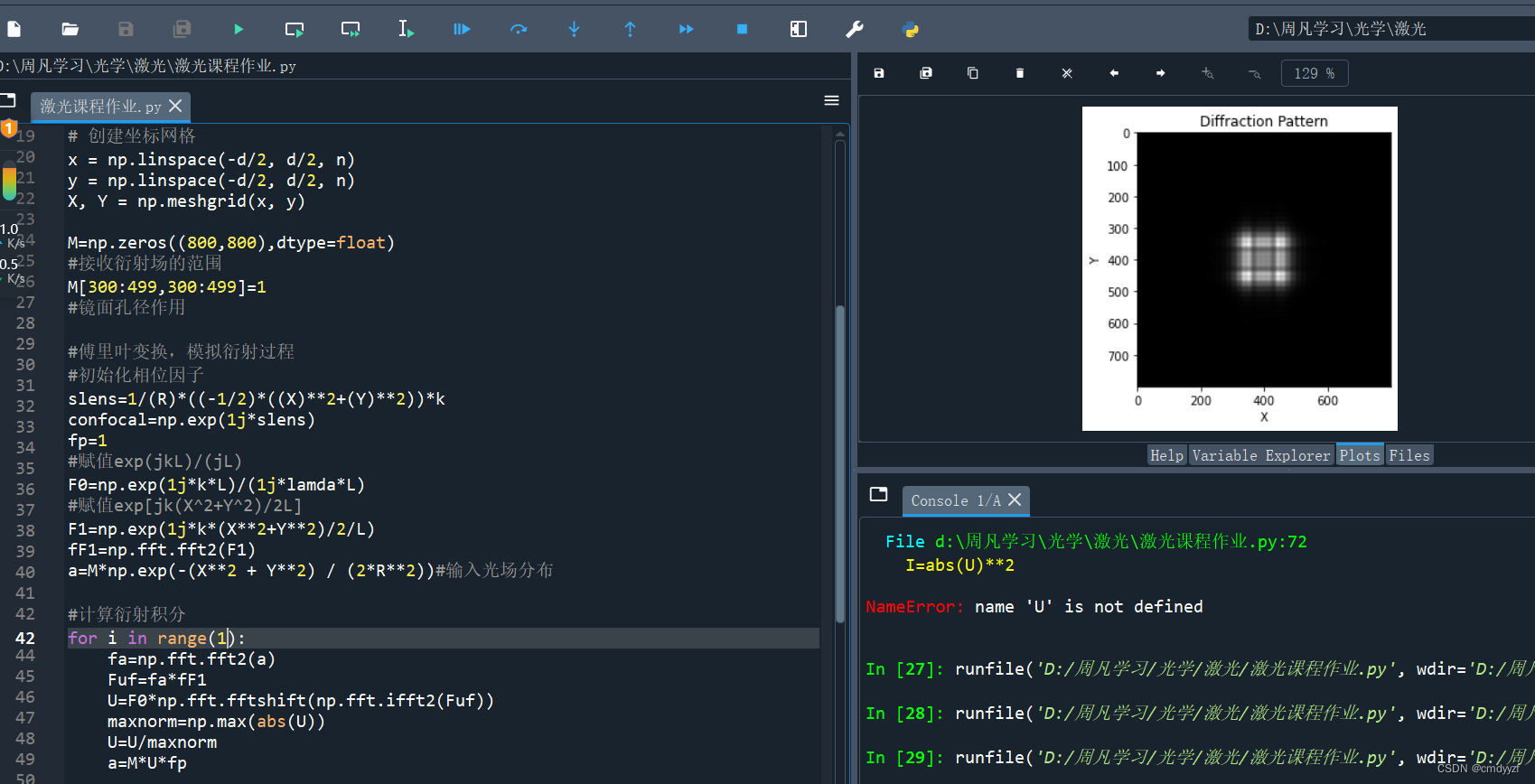
次数1

次数3

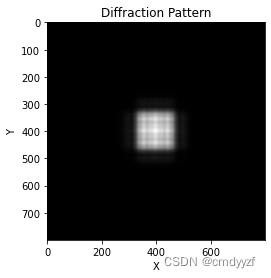
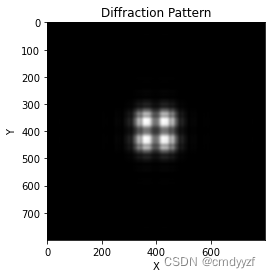次数2                                    

次数5

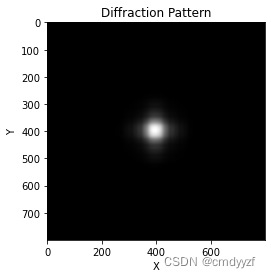
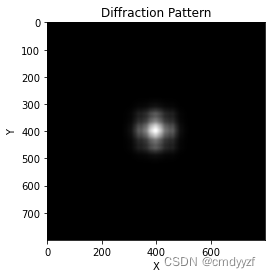次数4

可见刚开始若干次单程衍射的图案都不一样，

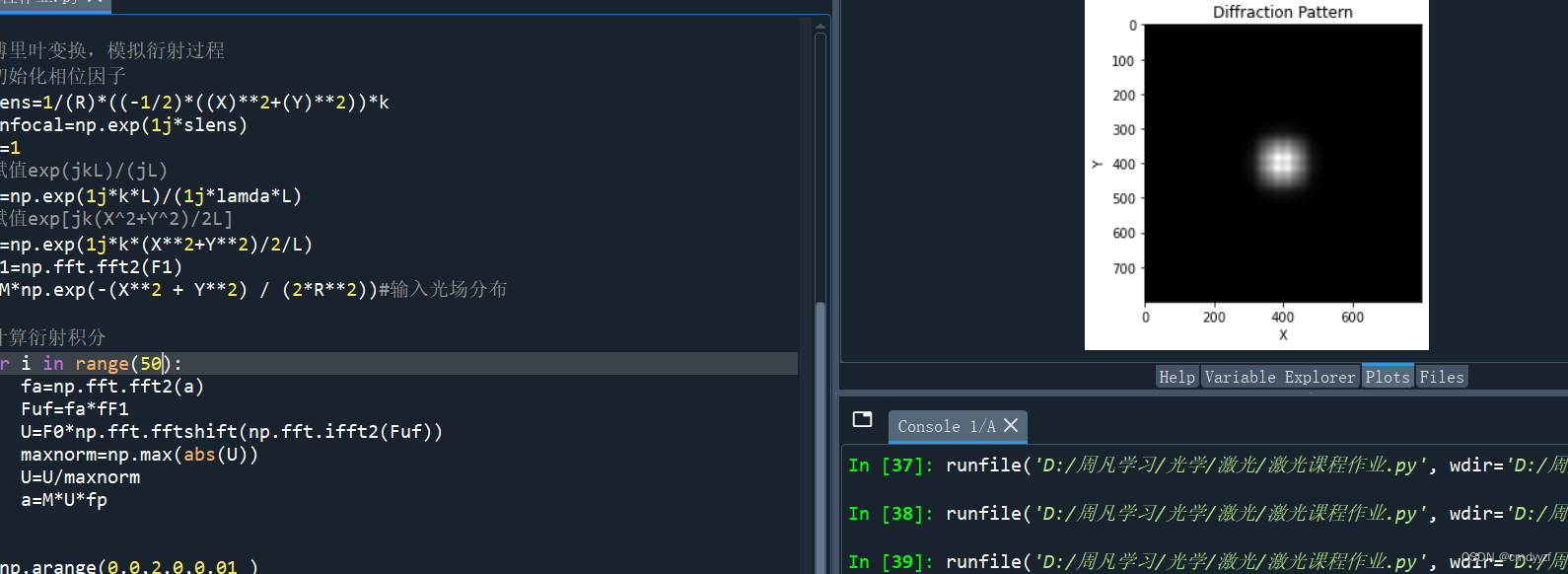
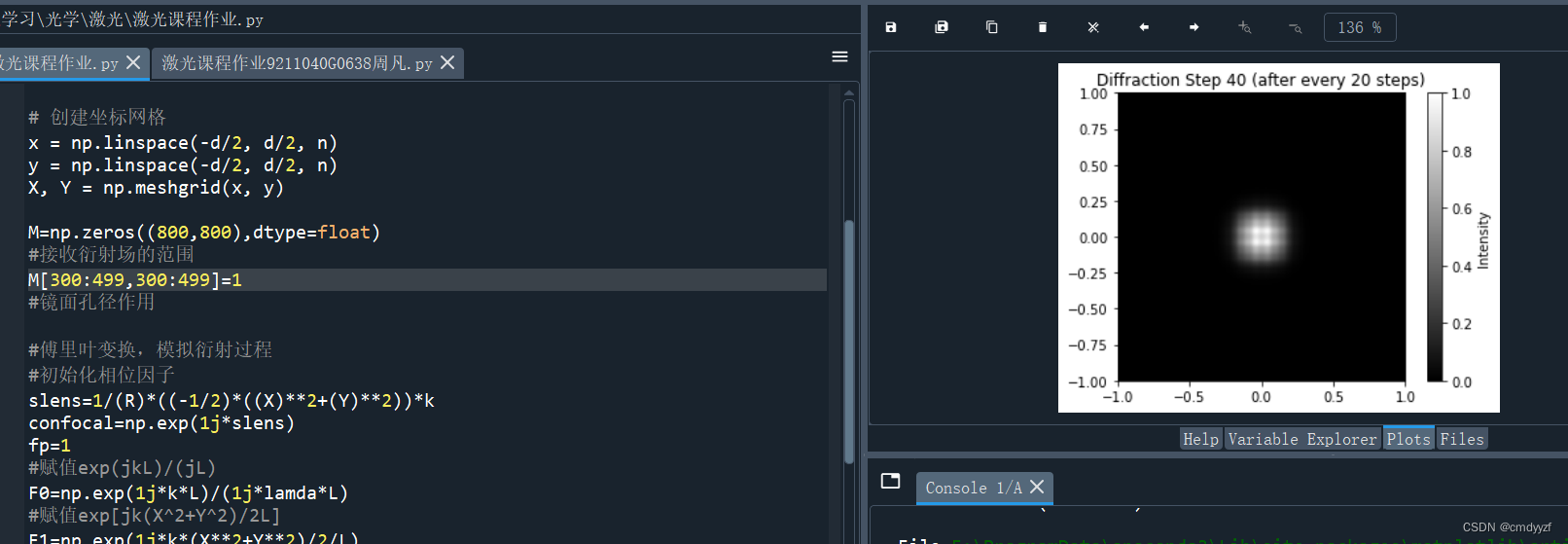
图像在30-40次之间开始趋于稳定

1. 光强随衍射次数的变化

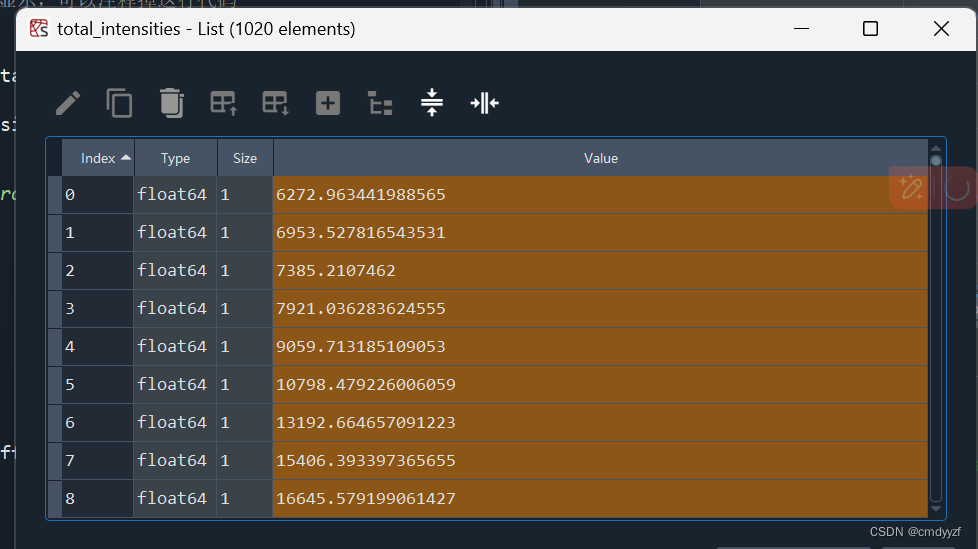
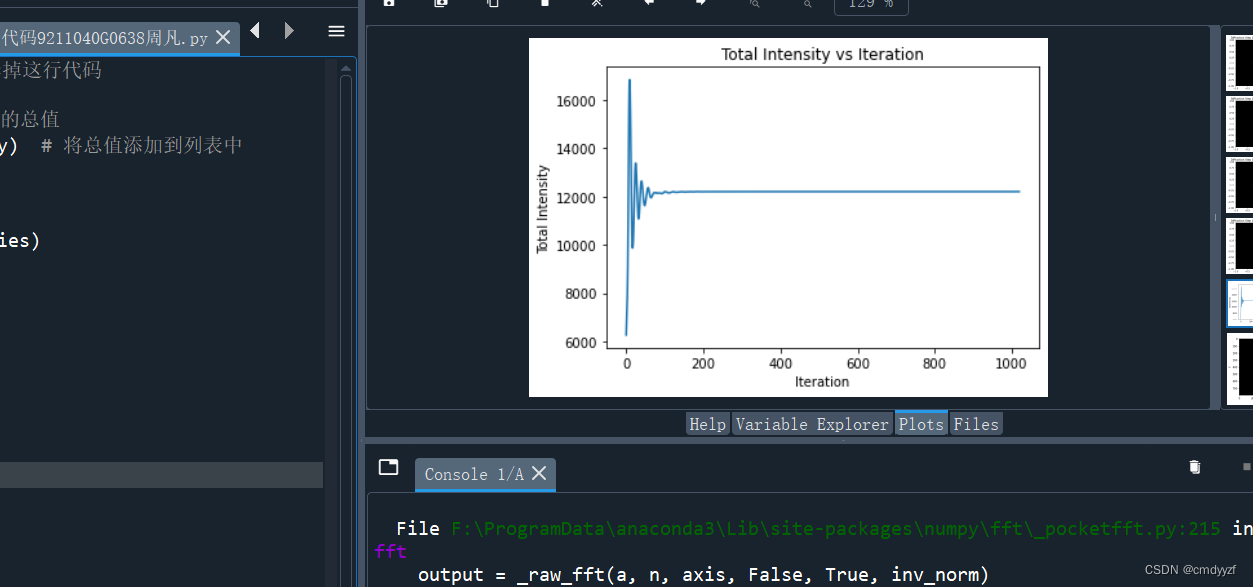
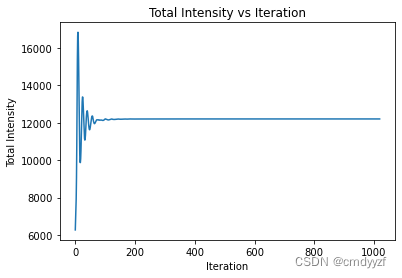
可见光强迅速增大达到峰值，经过震荡后然后渐渐趋于稳定。

3.改变a的值

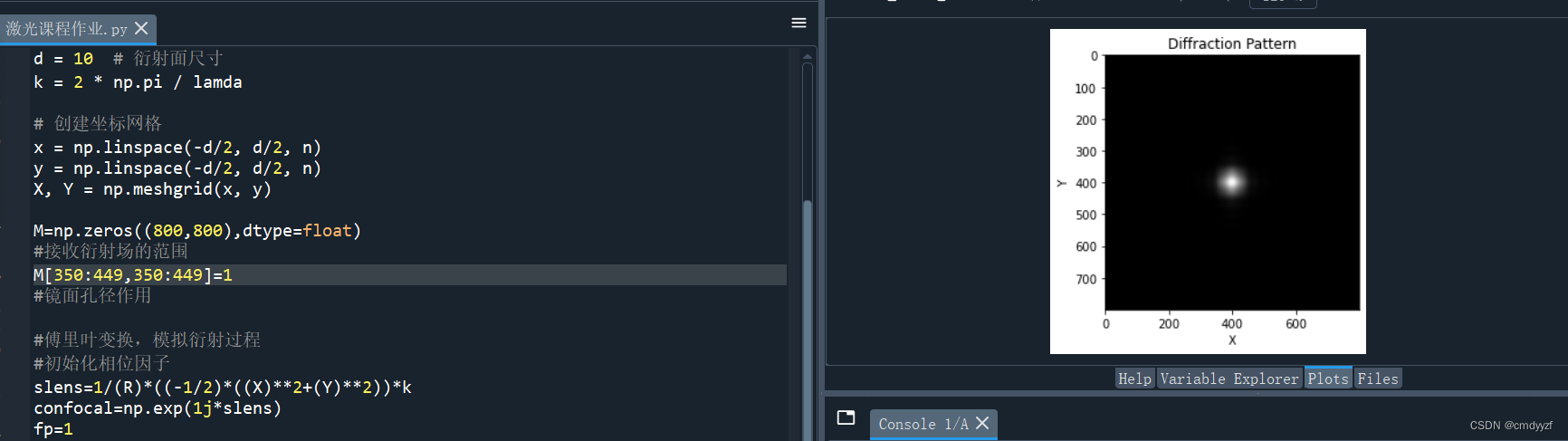
缩小a的值由100到50，衍射图案缩小且发生变化。

图像在20次左右便趋于稳定（也可能是由于图像太小不好观察的缘故）

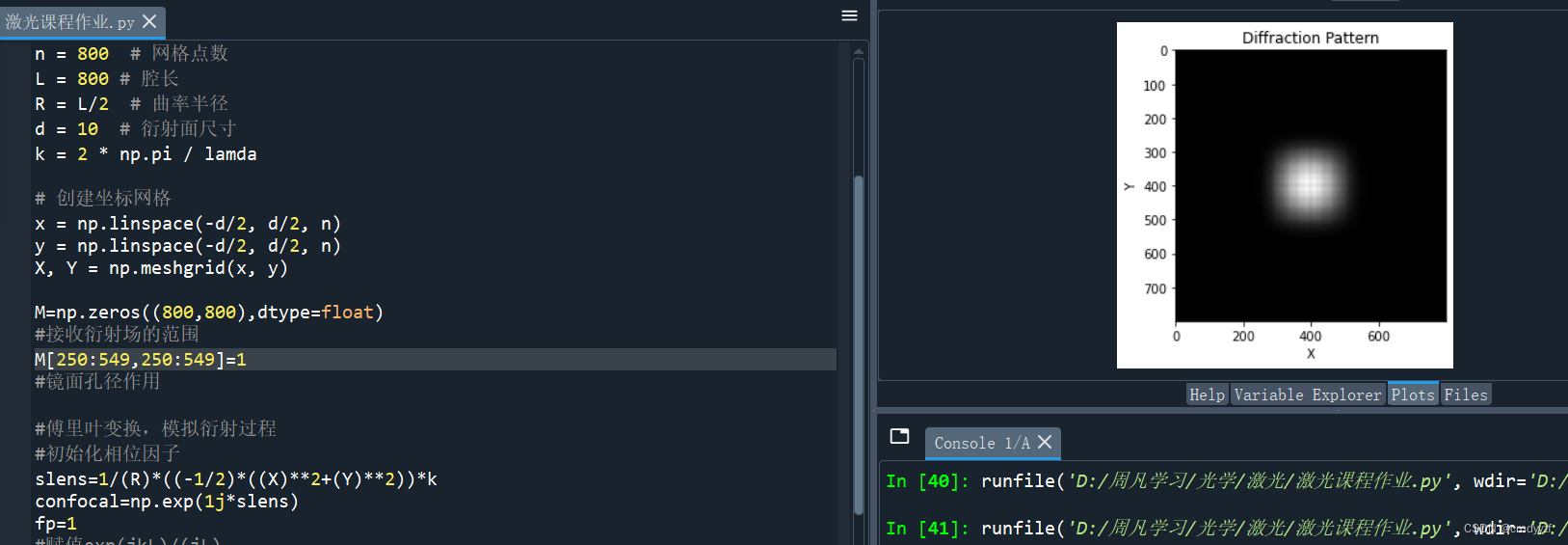
增大a由100到150，衍射图案放大且同样发生变化。

观察到衍射图案在80到100次左右趋于稳定

可见，衍射光强分布明显受到a的取值影响。