寻找单向环形链表的交点（C语言）

听说这题还是挺有逻辑性的，我们来看看吧

题目

/** * Definition for singly-linked list. * struct ListNode { *     int val; *     struct ListNode *next; * }; */`struct ListNode *detectCycle(struct ListNode *head) {}`

链接：https://leetcode-cn.com/problems/linked-list-cycle-ii/

示例

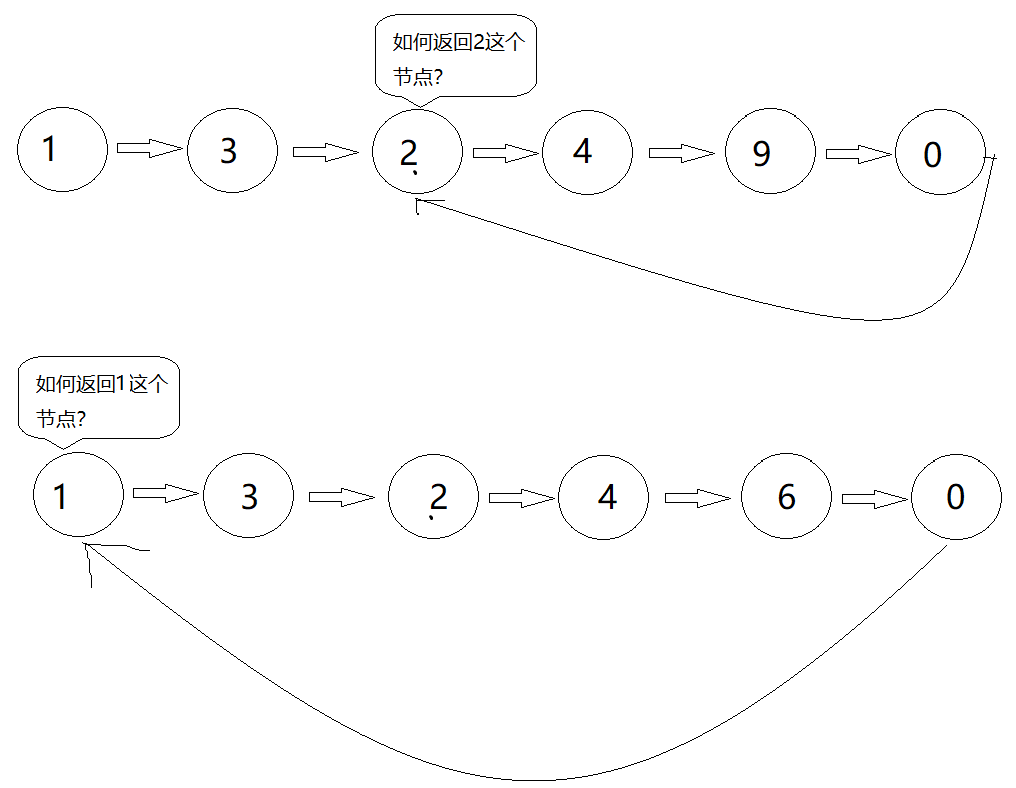
分析

思路一：

我们可以利用快慢指针，慢指针每次走一步，快指针每次走两步，如果这个单向链表无环，则慢指针永远都追不上快指针；但是如果有环，就必定在某一点上回相遇；

证明一下为什么快慢指针一定会相遇：

首先快指针一定比慢指针先进环，假设慢指针刚好到环的起点第一个位置，例如示例中“2”的位置，那么他们差的距离记作X，按照刚刚的逻辑“慢指针每次走一步，快指针每次走两步”，X每次就减少一，那么X作为一个整数，当X = 0时，慢指针跟快指针差距为0，不就是相遇了。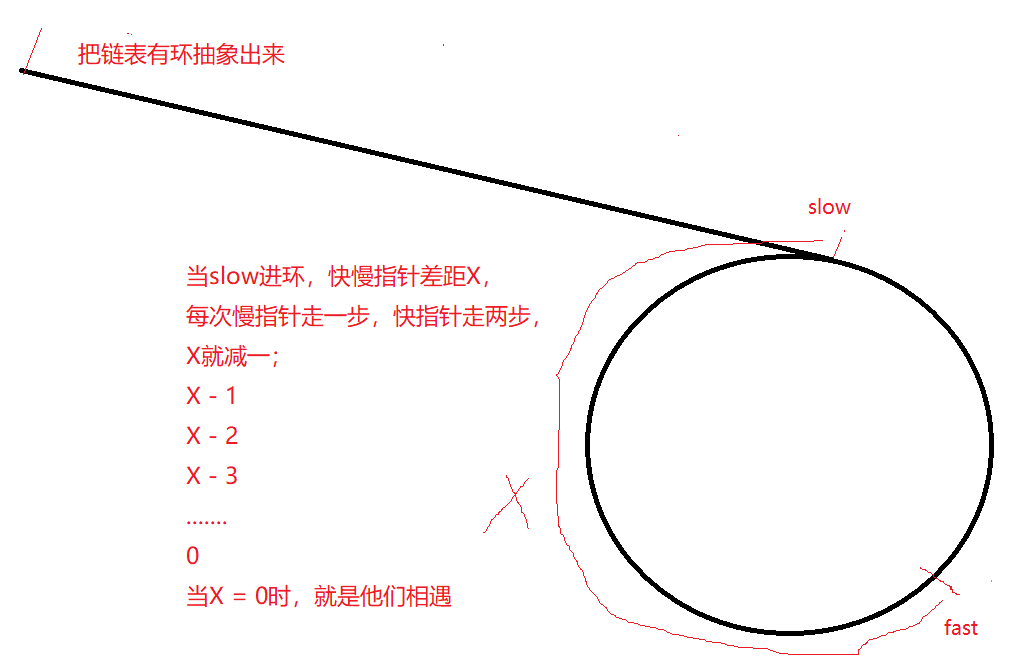

继续刚刚的相遇，若相遇，则我们把相遇的点断开，那么环就变成了相交的链表，最后我们就可以按照相交链表的求法来解决这个问题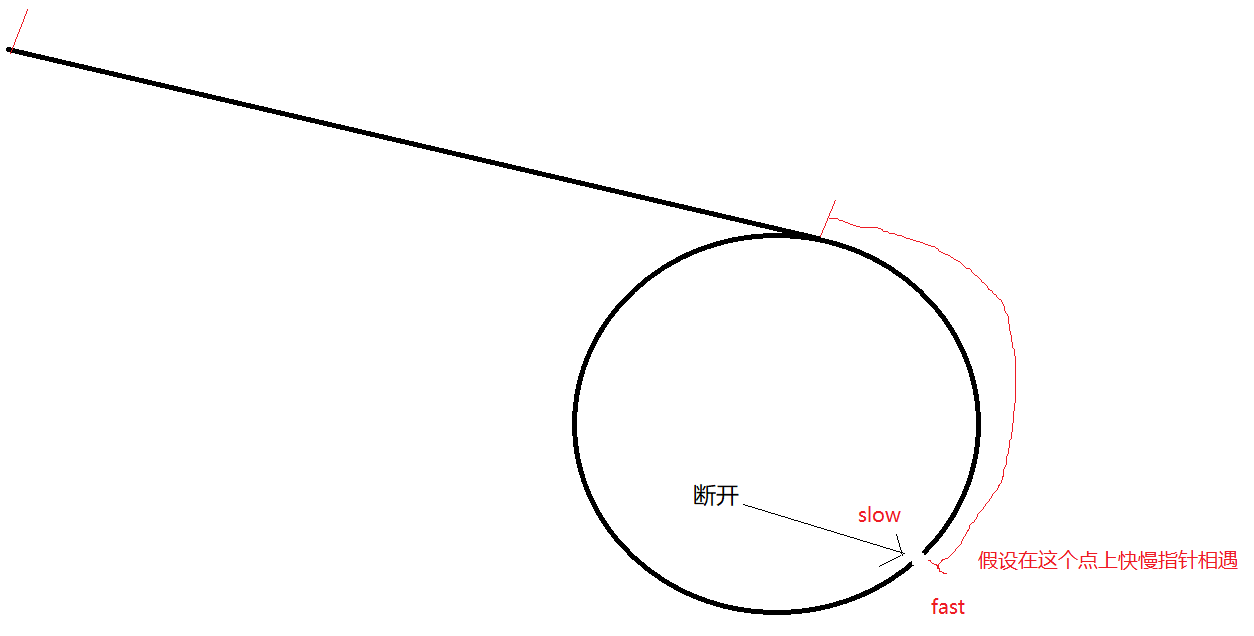

总结

这个方法写起来复杂，但理解起来很简单，断开这个具体的操作就是把相遇点的下一个节点记录，然后把相遇点指向NULL即可，相交链表问题就是长的链表 湖南党性培训 www.gxganxun.cn 可以先走上两链表的长度差值步，然后再比较节点地址即可

思路二：

还是用快慢指针，如果有环必相遇，如果没环结束。但是这次我们相遇后，让这个链表的头结点开始移动，fast/slow指针任意一个移动，计较，最后必定会走到同一个点上，而这个点就是我们要找的

证明：

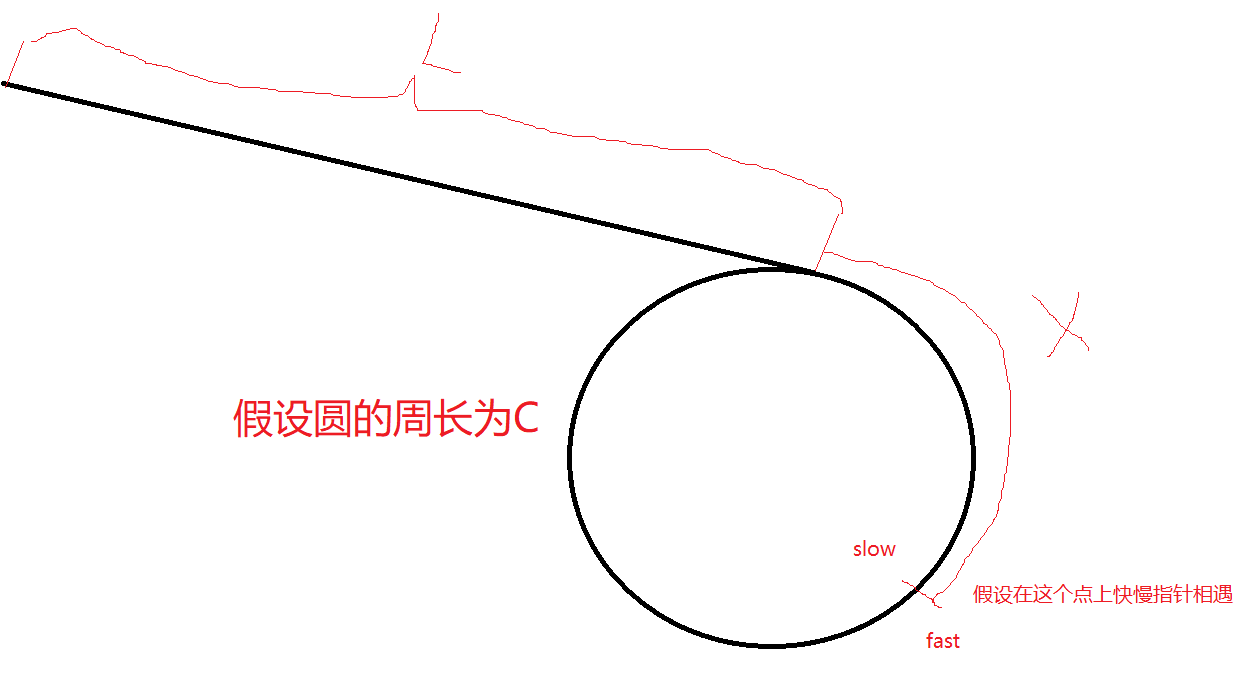
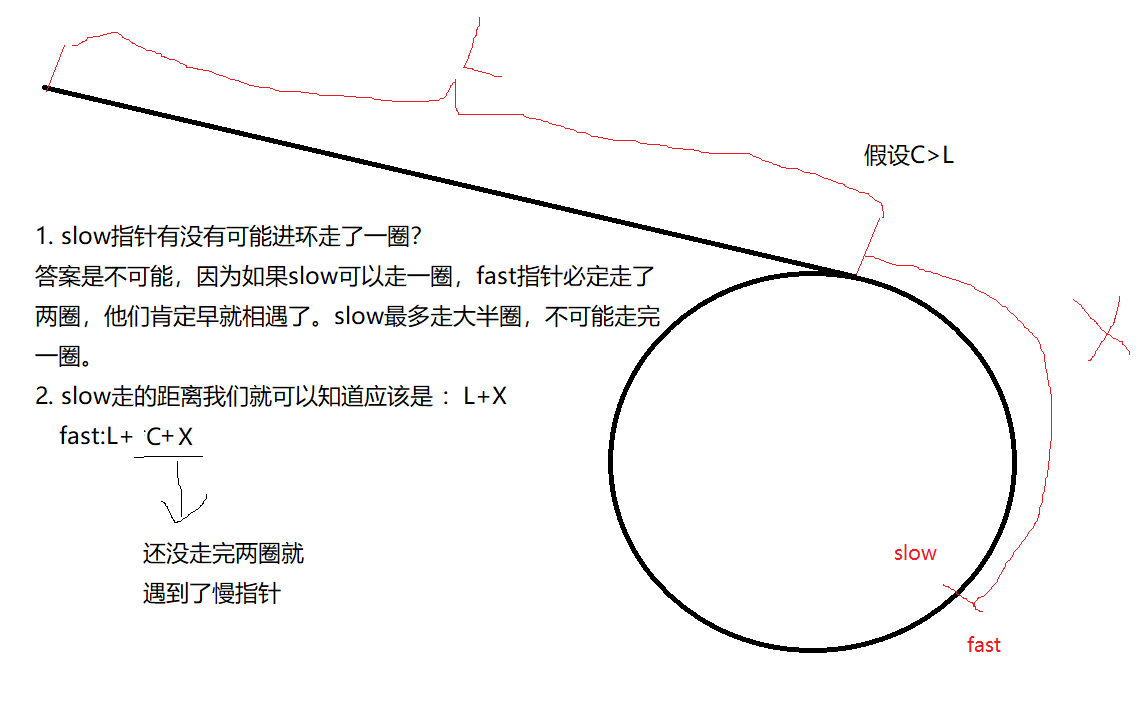
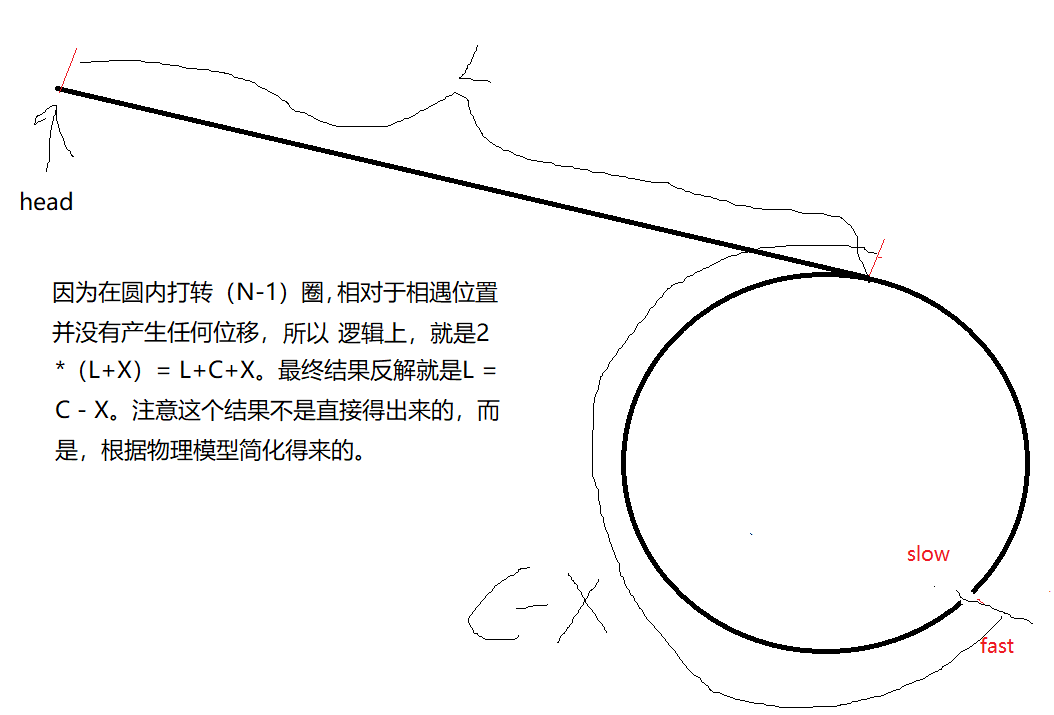
总结

这个代码好写，但是理解起来不容易，值得反复观看这个过程。

思路二的代码

typedef struct ListNode Node;struct ListNode *detectCycle(struct ListNode *head) {    Node* slow = head;    Node* fast = head;    while (fast && fast->next)    {        fast = fast->next->next;        slow = slow->next;        if (fast == slow)        {            Node* intersection = slow;            while (intersection - head)//有环，头走，slow跟fast的交点走，相同就是环的起点            {                intersection = intersection->next;                head = head->next;            }            return intersection;        }    }    return NULL;//无环}

如果看完对你有一点启发，可以点个赞吗？感谢！

更新
2022.3.11
10：17