Update:
2021年12月30日14点28分:增加了错题集和修改原先部分内容
错题集
队列和栈虽然都是单向插入的数据结构,但是如果没有头结点,第一次插入的时候要认为是尾部插入,所以尾指针可能修改
二分的时候r=mid-1,l=mid+1
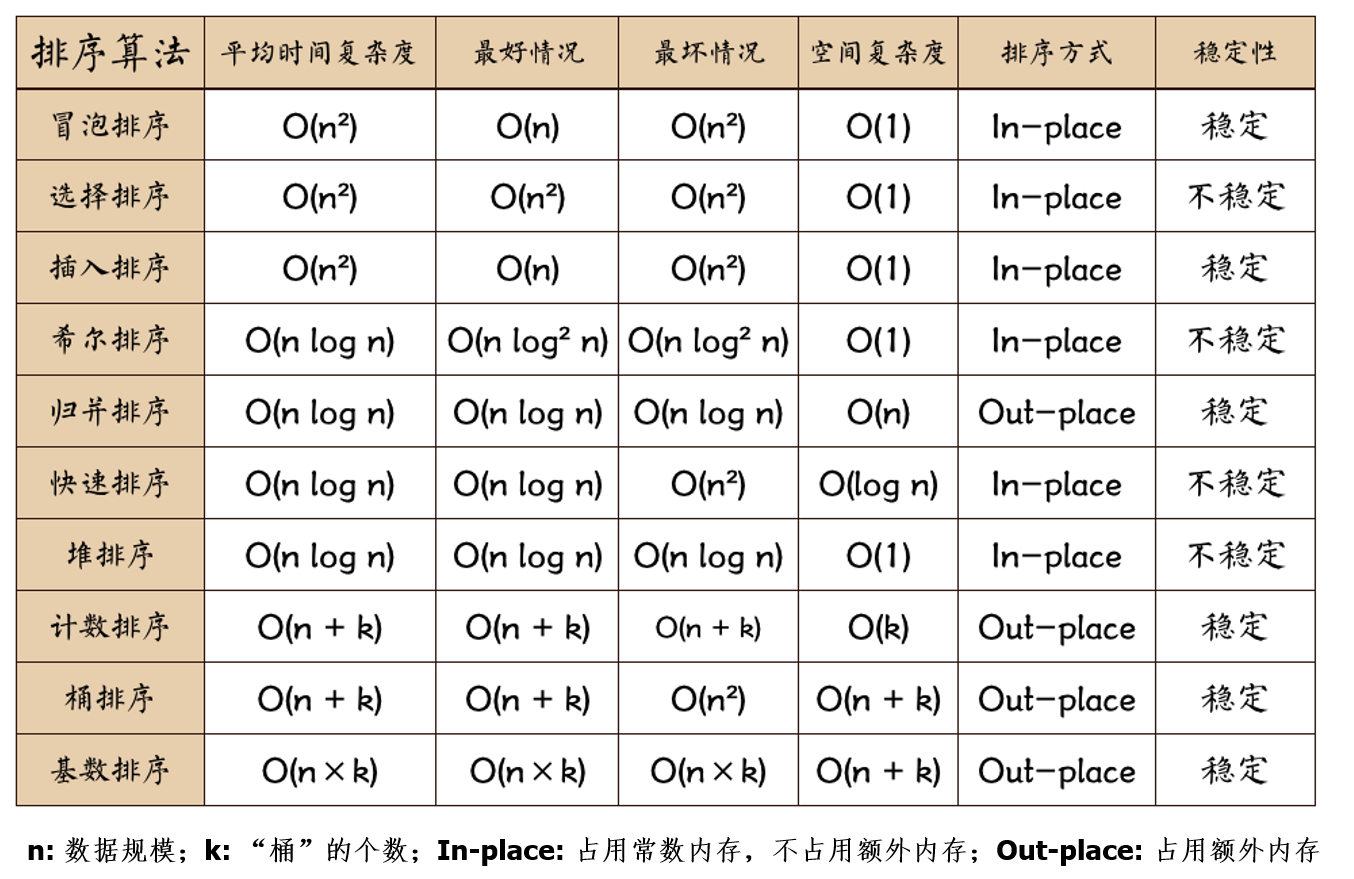
快速排序递归用栈,栈大小约为O(logn)O(logn)O(logn)
关键路径部分定义:




关于栈求表达式

关键路径的问题:
求vl时,如果有多条边指向一个点,减完之后要去min。如果选max,会导致时间超过一条边连接的事件的vl,导致超过了那个事件的最迟时间,不能完成,故选min。
稀疏矩阵快速转置算法理解:

一些概念
ACN(average comparing number):平均比较次数,ACN=∑i=0n−1pi×ciACN = \sum_{i=0}^{n-1}p_i\times c_iACN=∑i=0n−1pi×ci,其中pip_ipi是搜索第i项的概率,cic_ici是找到时的比较次数
AMN(average moving number):平均移动次数,计算方法同上
存储密度:d = 数据元素的值所需的存储量 ÷\div÷ 该数据元素所需的存储总量,因为可能有指针等非数据元素的值占用空间
稀疏因子:e=sm×ne=\frac{s}{m\times n}e=m×ns,s为分零元素个数,矩阵为m×nm\times nm×n的
EPL:树的外部路径长度,等于各叶节点到根节点的路径长度之和
IPL:树的内部路径长度,等于非叶节点到根节点的路径长度之和
PL:树的路径长度,PL=EPL+IPLPL = EPL + IPLPL=EPL+IPL
WPL:带权路径长度之和,WPL=∑i=1nwi×liWPL=\sum_{i=1}^nw_i\times l_iWPL=∑i=1nwi×li,其中第i个外结点的权值为wiw_iwi,它到根的路径长度为lil_ili,则该外结点到根的带权路径长度为wi×liw_i\times l_iwi×li
扩充二叉树的带权路径长度定义为树的各外结点到根的WPL
ASL(average search length):平均搜索长度,ASL=∑i=1npi×ciASL=\sum_{i=1}^n p_i\times c_iASL=∑i=1npi×ci,pip_ipi为搜索表中第i个元素的概率,cic_ici为找到给定关键码的比较次数,分success和failure
结点的平衡因子bf:右子树的高度-左子树的高度
跳表:有一组分层的链,0层链有n个元素,0级链的2k,2×2k,3×2k,...2^k,2\times 2^k,3\times 2^k,...2k,2×2k,3×2k,...个结点链接成为k−1k-1k−1级链,取元素所在最高级。根据跳表的分级,进行折半搜索。
装载因子:α=nm\alpha = \frac{n}{m}α=mn,m为散列表的空间大小,n为填入散列表中的记录数。一般α\alphaα控制在0.6~0.9之间,临界值是0.5,大于临界值,性能会急剧下降
B树:1层1个结点,2层至少2个结点,3层至少2⌈m2⌉2\lceil \frac{m}{2} \rceil2⌈2m⌉个结点,4层至少2⌈m2⌉22\lceil \frac{m}{2} \rceil^22⌈2m⌉2个结点……除根结点,每层至少⌈m2⌉\lceil \frac{m}{2} \rceil⌈2m⌉个结点,每个结点里最多m-1个值,最少⌈m2⌉−1\lceil \frac{m}{2}\rceil-1⌈2m⌉−1个。根节点至少2棵子树。2-3树m=3,2-3-4树m=4……。失败结点共n+1个。
优先队列:优先权数字越小,优先权越高
小问题
判断字符串是否为回文串:字符串每个字符进入栈和队列,同时从栈顶和队头取元素,并判断是否相等
三对角矩阵(主对角线和相邻的上下两条对角线上有值,其余为0):A[i][j]A[i][j]A[i][j]在数组B[i]B[i]B[i]存放于第kkk个,则i=⌊k+13⌋,j=k−2×ii= \lfloor \frac{k+1}{3} \rfloor , j=k-2\times ii=⌊3k+1⌋,j=k−2×i
广义表的长度:分几大块(原子和子表都只算一个);广义表的深度:括号的最大嵌套次数
二叉树中序遍历的直观方法:投影法。按照合适的大小将每个点分开,垂直投影到水平直线上,得到的顺序即为中序遍历序
二叉树遍历序:按照dfs遍历整颗二叉树(即先根节点,再左节点,再右节点的顺序),第一次访问的顺序排列为先序,第二次为中序,第三次为后序。实现的时候需要记录每个结点访问次数,以及叶节点的处理方法。
红黑树的三个特性:根节点和外部结点都是黑色结点;从根结点到外部结点的路径上,不允许出现两个连续的红色结点;所有从根结点到外部结点的路径上都有相同数目的黑色结点。
按秩启发式合并并查集时间复杂度:find:O(nlogn)O(nlogn)O(nlogn),树高限制在logn内
并查集合并路径压缩的非递归写法,以及优化后的并查集时间复杂度计算
哈希函数取模的选择:≤n\leq n≤n的(最大)素数,n为hash表长度
哈希冲突的解决方法:闭散列方法(存储到表的另一个位置),开散列方法(存在散列表主表之外),双hash,公共溢出区(冲突的都放入此表)
折半插入的时间复杂度:O(n2)O(n^2)O(n2),虽然减少了比较次数,但是移动次数仍不变,所以复杂度仍是平方级别
希尔排序:时间复杂度O(n32)O(n^{\frac{3}{2}})O(n23)
设置“监视哨”简化边界判断可以节省时间
树(森林)后根遍历等于对应二叉树的中序遍历
带图
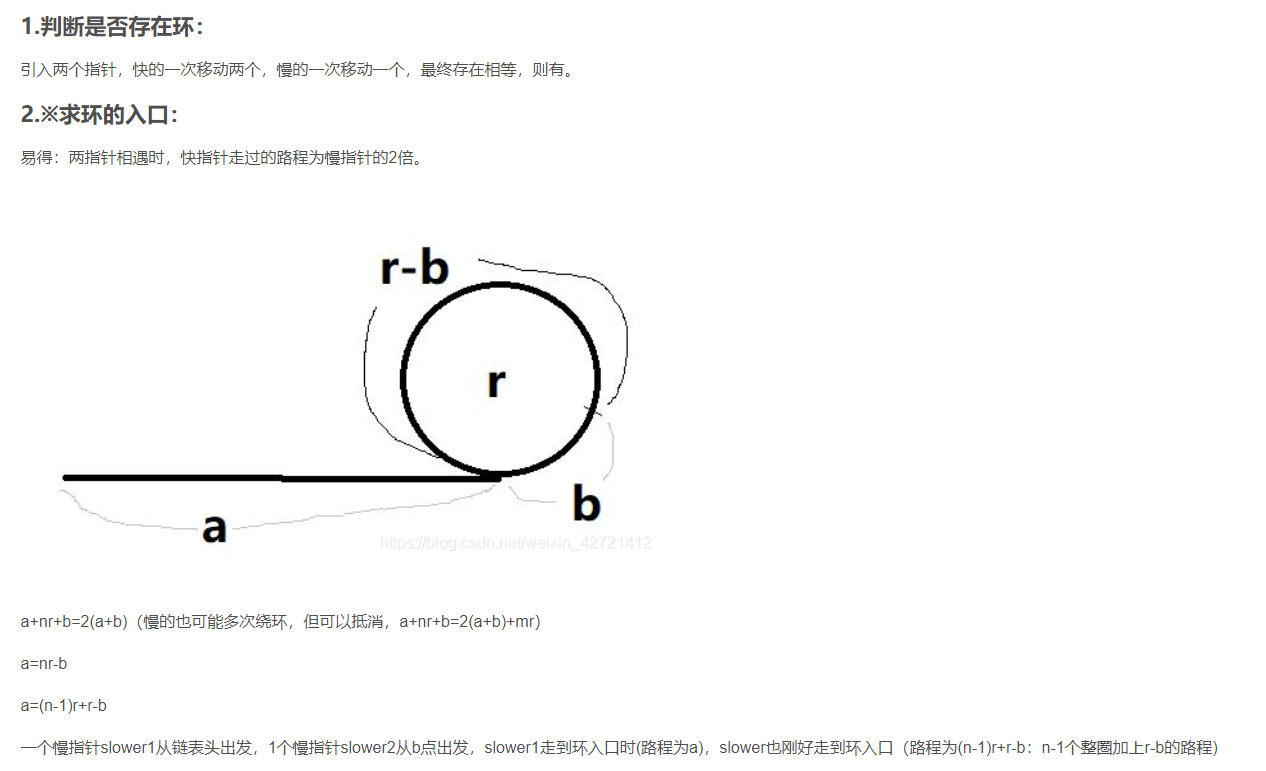
如何判断单链表中有环?快慢指针法。如何找到环的入口?
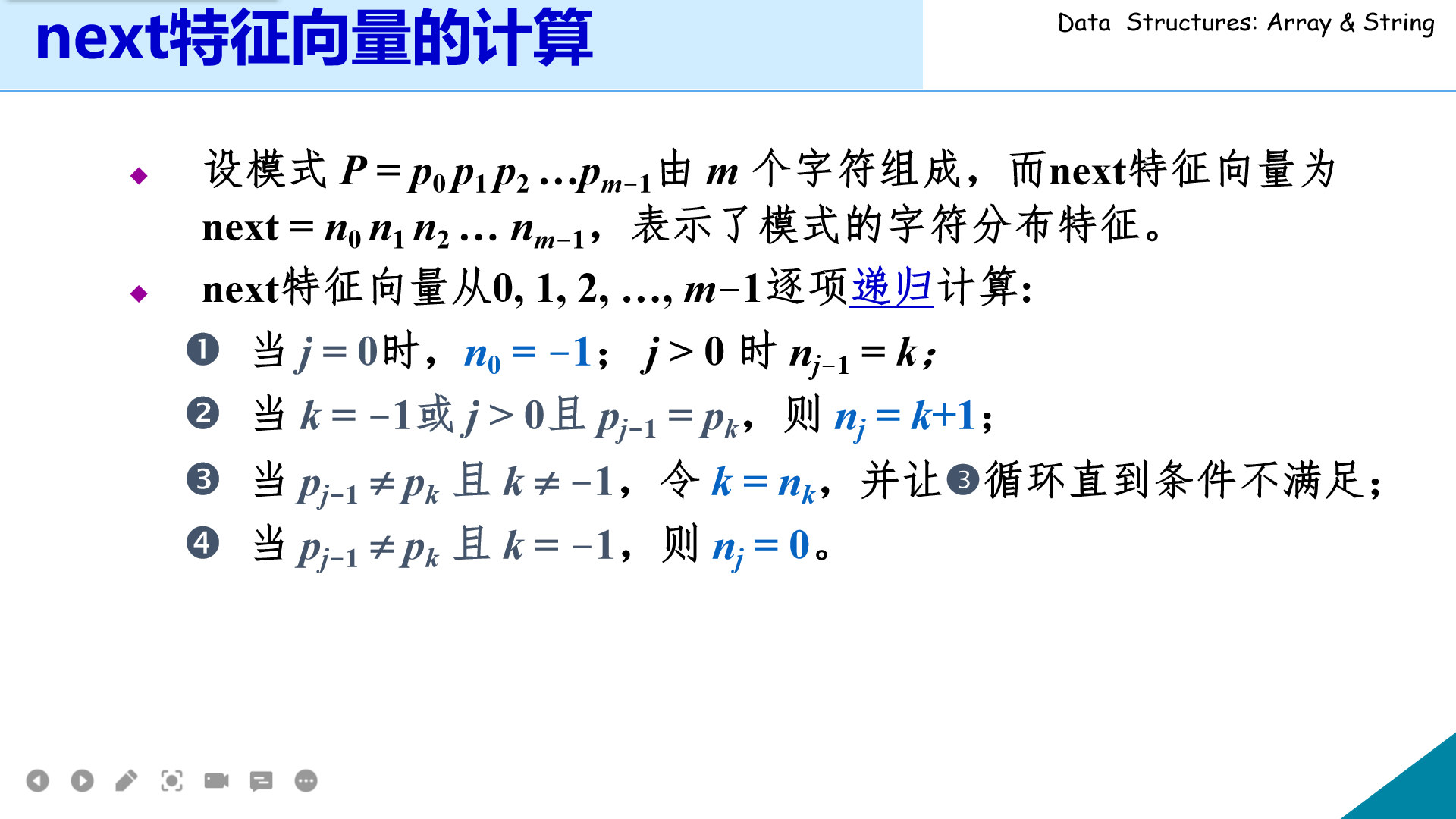
KMPnext数组的计算算法
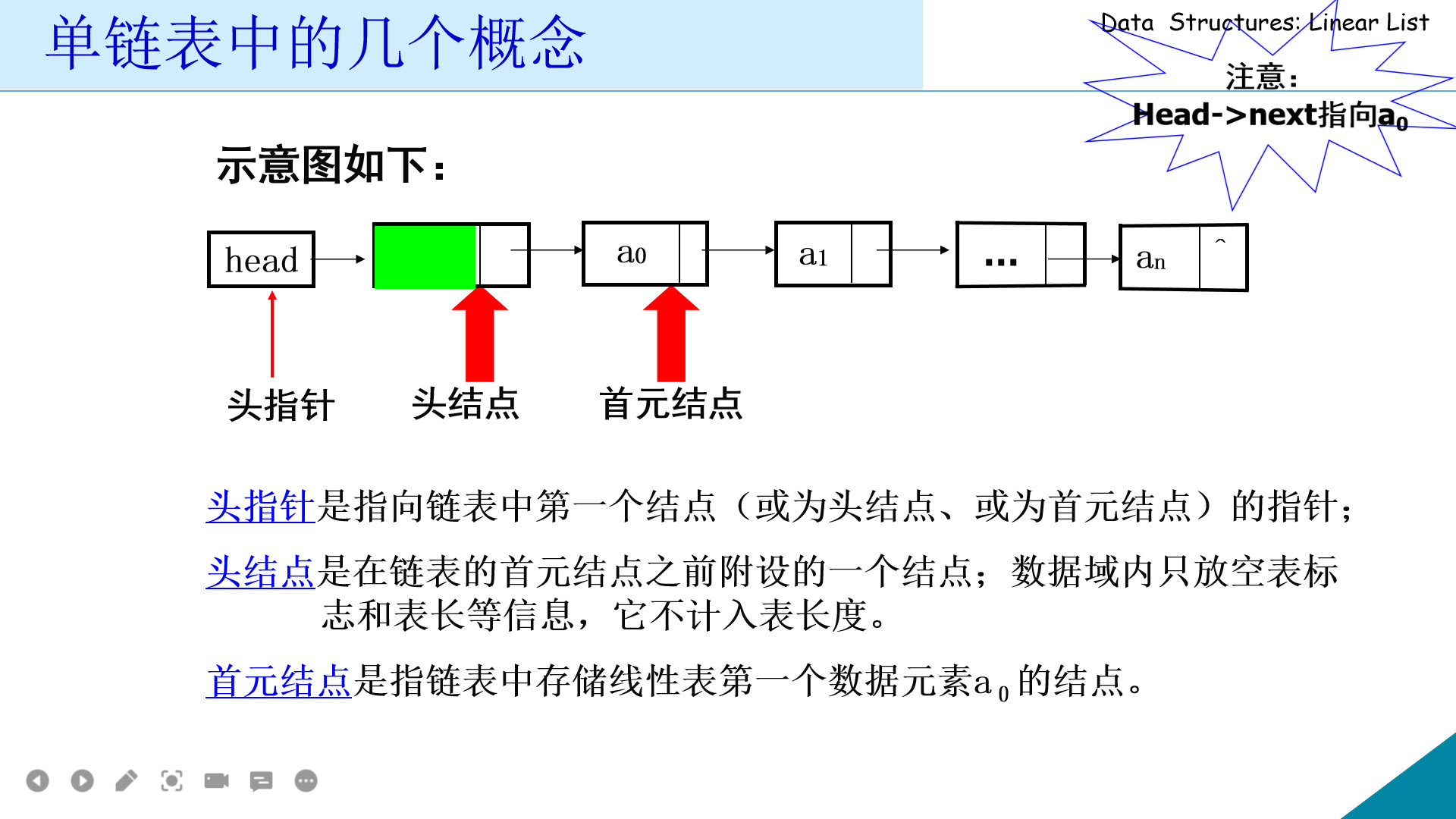
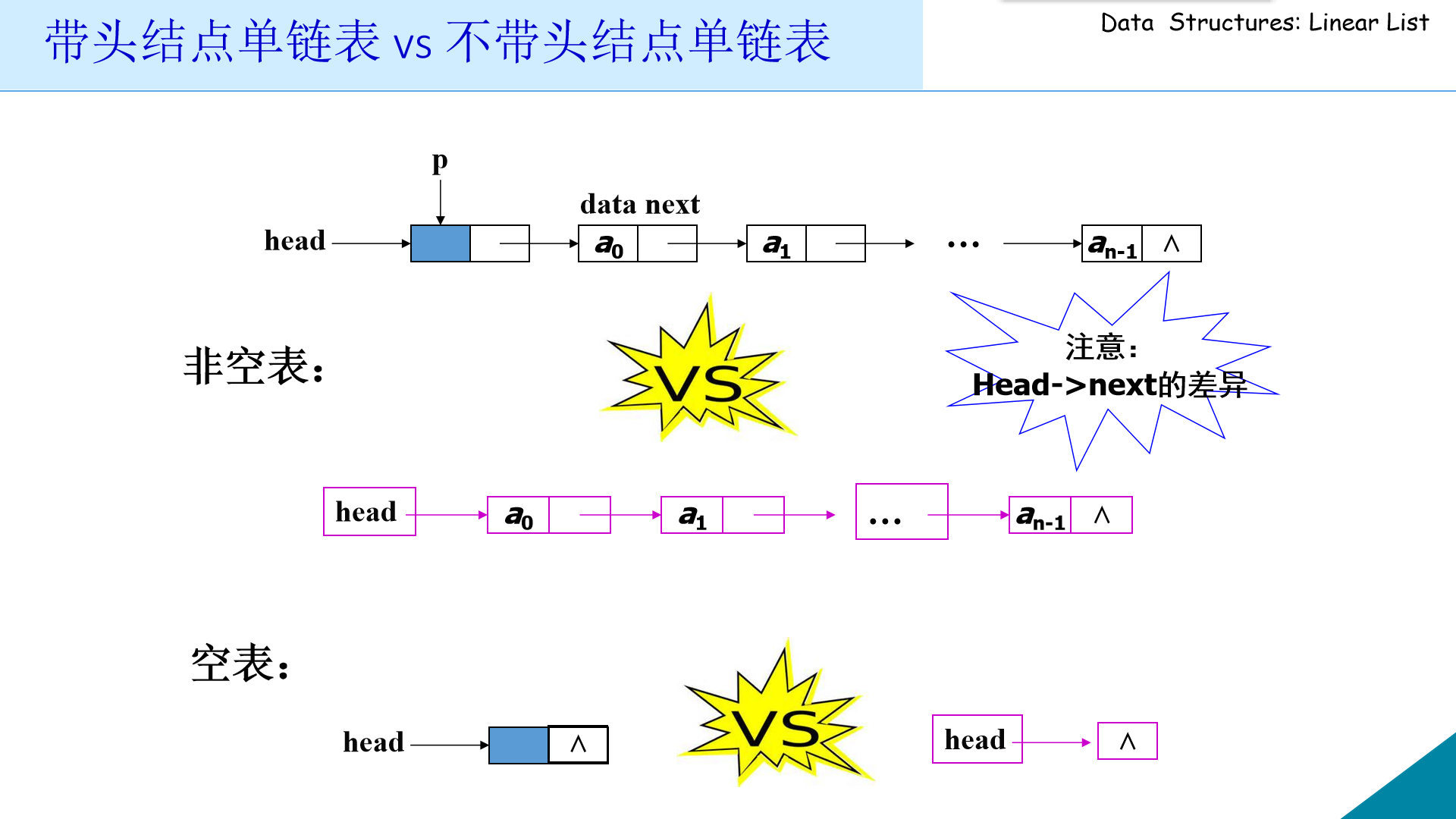
单链表的头指针:
卡特兰数计算式及其应用:

ASL与转载因子α\alphaα的关系:

B+树:

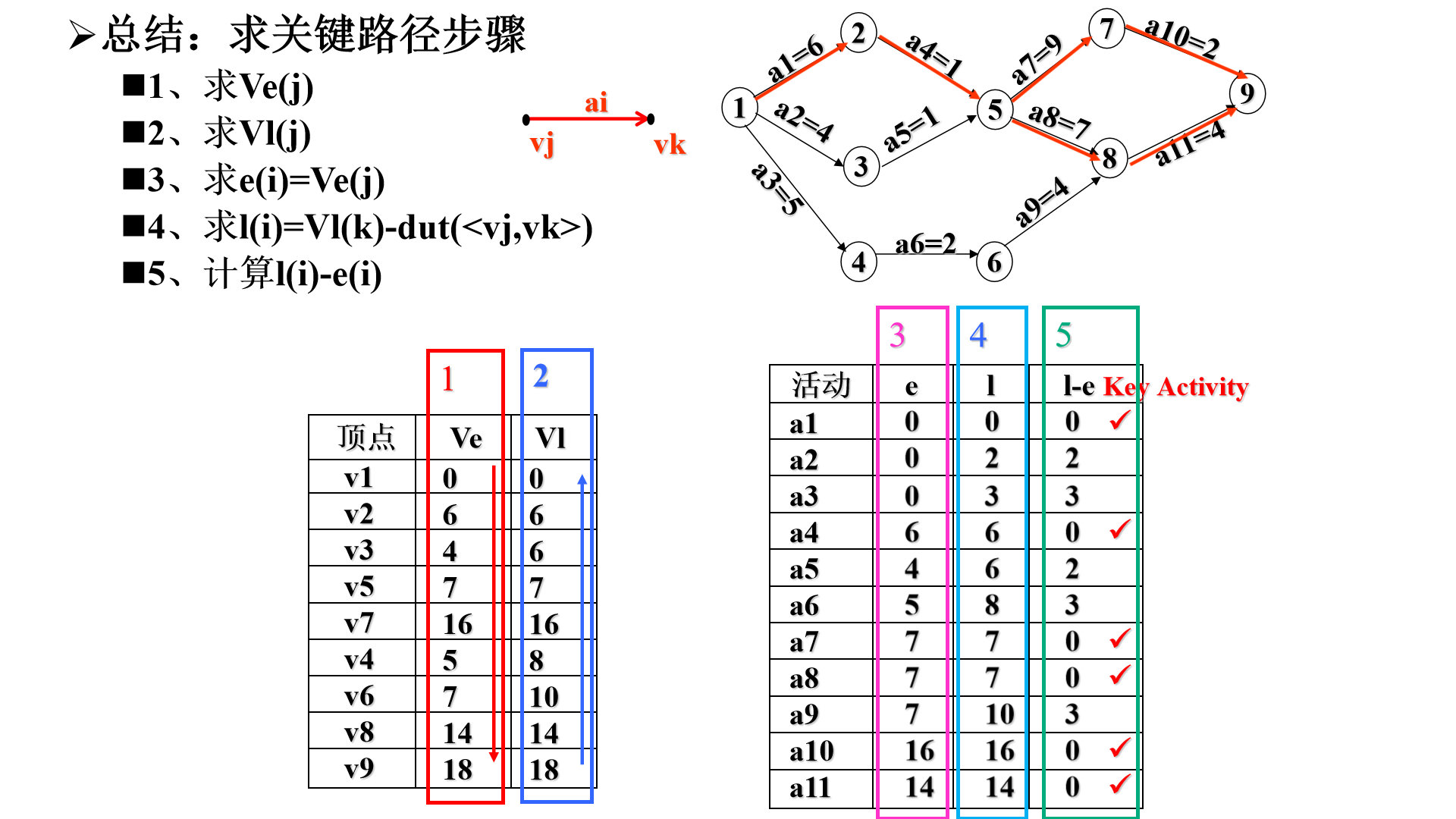
求关键路径的步骤:
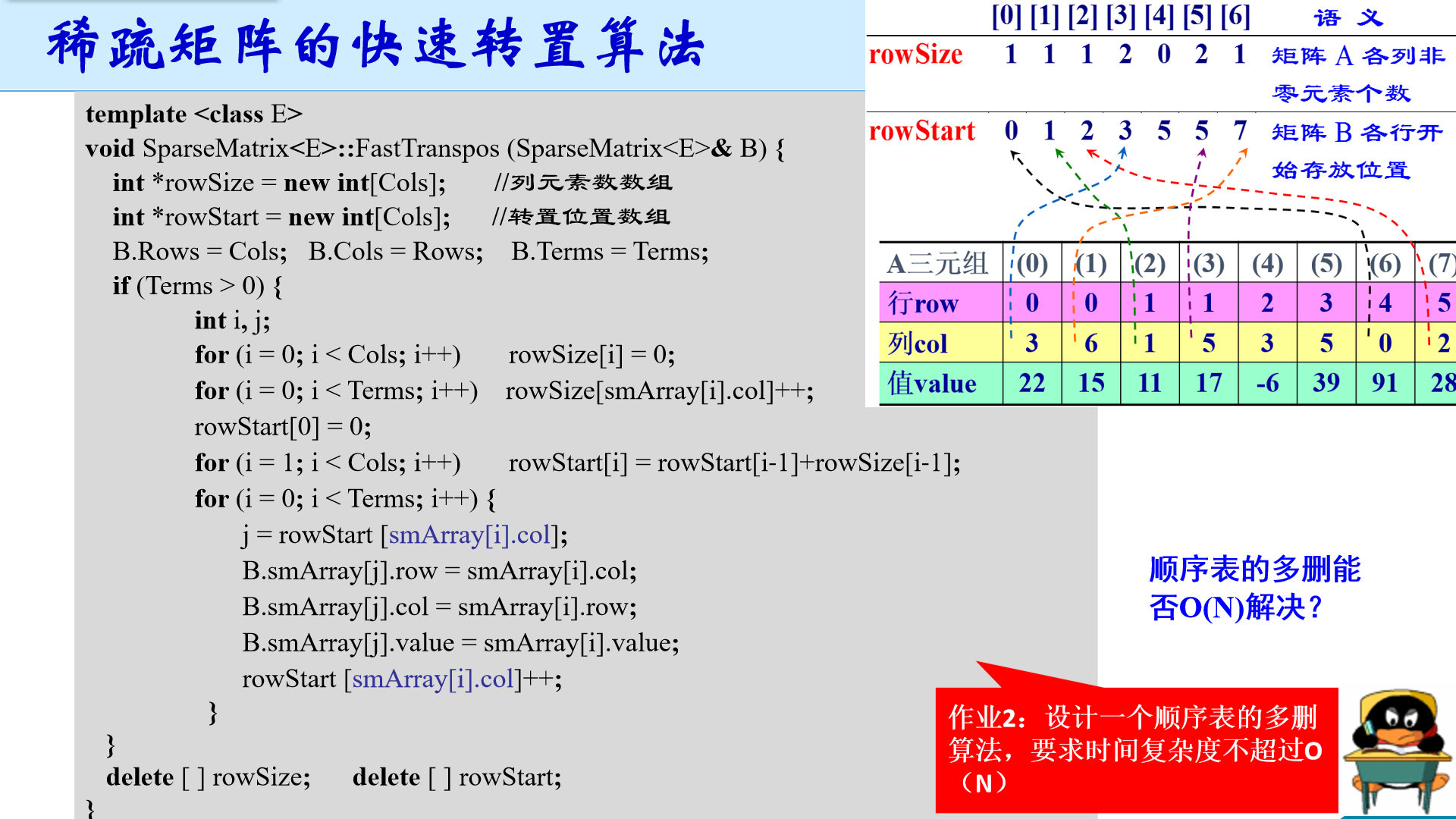
稀疏矩阵的快速转置算法:
其他
递归算法转非递归算法
B树结点的删除:注意满足B树的性质。
线索化二叉树:如果没有左儿子,就指向前驱结点;如果没有右儿子,就指向后继结点。
哈希的数字分析法





 这篇博客深入探讨了数据结构中的栈、队列、二分查找、快速排序和关键路径等问题,以及算法优化如平均比较次数和平均移动次数的计算。还涉及了稀疏矩阵转置、哈希表、B树、优先队列等,并讲解了判断链表环、字符串回文、KMP算法等实用技巧。同时,文章提到了红黑树的特性以及并查集的时间复杂度分析。
这篇博客深入探讨了数据结构中的栈、队列、二分查找、快速排序和关键路径等问题,以及算法优化如平均比较次数和平均移动次数的计算。还涉及了稀疏矩阵转置、哈希表、B树、优先队列等,并讲解了判断链表环、字符串回文、KMP算法等实用技巧。同时,文章提到了红黑树的特性以及并查集的时间复杂度分析。


















 1123
1123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










