layer normalization+残差连接+矩阵的低秩的含义

embedding 是学习得来的，emmbedding并不存在一个客观的分布。通过layer normalization得到的embedding是 以坐标原点为中心，1为标准差，越往外越稀疏的球体空间中。
https://www.zhihu.com/question/395811291/answer/1260290120?ivk_sa=1024320u

https://zhuanlan.zhihu.com/p/42833949
作者们认为神经网络的退化才是难以训练深层网络根本原因所在，而不是梯度消散。虽然梯度范数大，但是如果网络的可用自由度对这些范数的贡献非常不均衡，也就是每个层中只有少量的隐藏单元对不同的输入改变它们的激活值，而大部分隐藏单元对不同的输入都是相同的反应，此时整个权重矩阵的秩不高。并且随着网络层数的增加，连乘后使得整个秩变的更低。
然是一个很高维的矩阵，但是大部分维度却没有信息，表达能力没有看起来那么强大。
残差连接正是强制打破了网络的对称性，提升了网络的表征能力。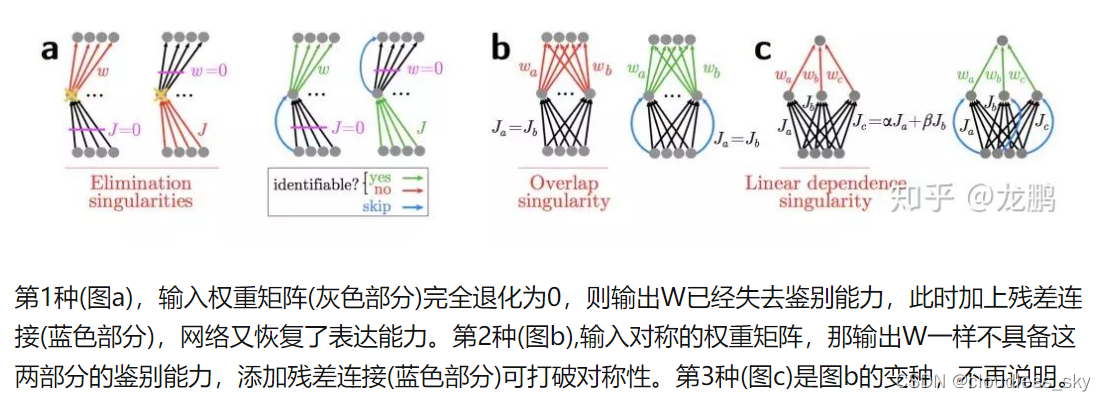

https://blog.youkuaiyun.com/qq_29762941/article/details/80722805
还记得我们怎么手工求矩阵的秩吗？为了求矩阵A的秩，我们是通过矩阵初等变换把A化为阶梯型矩阵，若该阶梯型矩阵有r个非零行，那A的秩rank(A)就等于r。从物理意义上讲，矩阵的秩度量的就是矩阵的行列之间的相关性。如果矩阵的各行或列是线性无关的，矩阵就是满秩的，也就是秩等于行数。回到上面线性方程组来说吧，因为线性方程组可以用矩阵描述嘛。秩就表示了有多少个有用的方程了。上面的方程组有3个方程，实际上只有2个是有用的，一个是多余的，所以对应的矩阵的秩就是2了。

   OK。既然秩可以度量相关性，而矩阵的相关性实际上就表示了矩阵的结构信息。如果矩阵之间各行的相关性很强，那么就表示这个矩阵实际可以投影到更低维的线性子空间，也就是用几个向量就可以完全表达了，它就是低秩的。所以我们总结的一点就是：如果矩阵表达的是结构性信息，例如图像、用户-商品推荐表等等，那么这个矩阵各行之间存在这一定的相关性，那这个矩阵一般就是低秩的。