本文深入探讨了贪心算法在解决硬币问题、区间问题、字典最小序问题等典型场景的应用，通过具体实例讲解了如何设计并实现贪心策略，以达到优化问题解决方案的目的。
贪心算法：
核心：不断贪心的选择当前最优策略
1.硬币问题
有1元、5元、10元、50元、100元、500元硬币各C1、C5、C10、C50、C100、C500枚。现要用这些硬币来支付A元，最少需要多少枚硬币？
限制条件：0<C,A<10^9
输入：
3,2,1,3,0,2 //每种硬币的个数
620 //总金额
输出：
6 //最少个数
解决方案： 优先尽可能多地使用面值大的硬币
#include<iostream>
using namespace std;
int main(){
int v[6]={1,5,10,50,100,500}; //面值数组
int c[6];
for(int i=0;i<6;i++){ //录入每面值的个数
cin>>c[i];
}
int sum; //总金额
cin>>sum;
int countt=0;
for(int i=5;i>=0;i--){ //尽可能从大面值开始
int n = min(sum/v[i], c[i]); //寻找每种面值需要的枚数
sum- = n*v[i]; //每种面值过后还剩的总金额
countt += n; //总枚数加上现在的
}
cout<<countt;
return 0;
}
2.区间问题
有n项工作，每项工作分别在Si时间开始，在Ti时间结束。对于每项工作，可以参加也可以不参加。求最多能参加多少项工作？
限制条件：
1<n<100000, 1<Si<Ti<10^9
输入：
n=5
S=1,2,4,6,8
T=3,5,7,9,10
输出：
3 //选择1,3,5
解决方案： 在可选工作中，每次选择结束时间最早的工作
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
int num;
cin>>num; //工作个数
pair<long long, long long> tim[num]; //定义元素为“坐标对”的数组tim
for(int i=0;i<num;i++){
cin>>tim[i].second; //录入各工作开始时间
}
for(int i=0;i<num;i++){
cin>>tim[i].first; //录入各工作结束时间
}
sort(tim,tim+num); //会以每个元素第一个值为标准进行排序
int countt=0;
long long a=0;
for(int i=0;i<num;i++){ //依次遍历每个工作
if(a<tim[i].second){ //选择最近的且开始时间比所选工作结束时间晚
a=tim[i].first; //结束时间成为新的开始时间
countt++;
}
}
cout<<countt;
return 0;
}
知识总结：
- pair<int, int> a[num],初始化一个元素为点对的数组a，a的长度为num
- a.first 元素的第一个值
a.second 元素的第二个值 - sort（a, a+num）,每元素第一个值为标准升序排列
3. 字典最小序问题
给定长度为N的字符串S，构造长度同为S的字符串T。起初，T是一个空串，随后反复进行下列任意操作：
从S头部删除一个元素，加到T尾部
从T头部删除一个元素，加到T尾部
目标：构造字典序尽可能小的字符串T
限制条件：
1<n<2000
字符串S只包含大写字母
输入：ACDBCB
输出：ABCBCD
解决方案： 设置收尾指针，从头部和尾部各取一个进行比较，如果不同，则选取小的放入新串，如果相同，则比较他们各自的下一个元素，选取小的那一端元素先行放入新串。
#include<iostream>
using namespace std;
int main(){
string str;
cin>>str; //输入字符串
int a=0,b=str.size()-1; //定义收尾指针
while(a<=b){
bool left=false;
for(int i=0;i<=b/2;i++){ //for循环用来判断当首尾相同时哪个更小
if(str[a+i]==str[b-i]) continue;
else
if(str[a+i]<str[b-i]){
left=true;
break;
}
break;
}
if(left) cout<<str[a++]; //输出首尾确定元素
else cout<<str[b--];
}
return 0;
}
4. Saruman’s Army
直线上有N个点，点i的位置是Xi。从这N个点中选择若干个加上标记，对于每一个点，其距离为R的区域内必须有标记点。求至少有多少点被加上标记？
限制条件：
1<N<1000 0<R<1000 0<Xi<1000
输入：
N=6
R=10
X=1,7,15,20,30,50
输出：
3 //7,20,30
解决方案：
要保证最左端的点，从最左端点开始向右距离为R的最远点进行标记，从此标记点开始，再向右找到距离为R的所有点，从下一个点开始，重复上述策略不断贪心
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
int num;
cin>>num; //点总数
int length;
cin>>length; //距离数
int a[num];
for(int i=0;i<num;i++){
cin>>a[i]; //录入坐标
}
sort(a,a+num); //将距离升序排列方便贪心
int countt=0;
int i=0;
while(i<num){
int s=a[i]; //当前最左端的点
i++; //从下一个点开始
while(i<num && a[i]<=s+length) i++; //寻找距离R内最远的点i-1进行标记
int t=a[i-1];
while(i<num && a[i]<=t+length) i++; //从标记点下一个点i开始，寻找距离外最近的点,继续贪心
countt++;
}
cout<<countt;
return 0;
}
5.Fence Repair
切割一段长L木板N块，每次切割的开销为这段木板的长度。如长度为21的木板，切成5,8,8长度的三段，切成13,8时，开销为21，再将13切成5,8，开销为13，总开销为13+21=34。求按照目标要求将木板切割完的最小开销。
限制条件：
1<N<20000 0<L<50000
输入：
N=3
L=8,5,8
输出：
34 //实例中的表述
解决方案：
#include<iostream>
#include<cstdio>
using namespace std;
int main(){
int num;
cin>>num;
int a[num];
for(int i=0;i<num;i++){
cin>>a[i];
}
long long sum=0;
while(num>1){
int min1=0,min2=1;
if(a[min1]>a[min2]) swap(min1,min2);
for(int i=2;i<num;i++){
if(a[i]<a[min1]){
min2=min1;
min1=i;
}
else if(a[i]<a[min2]){
min2=i;
}
}
int t=a[min1]+a[min2];
sum+=t;
if(min1==num-1) swap(min1,min2);
a[min1]=t;
a[min2]=a[num-1];
num--;
}
cout<<sum;
return 0;
}
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
int num;
cin>>num;
int a[num];
for(int i=0;i<num;i++){
cin>>a[i];
}
long long sum=0;
int i=1;
while(i<num){
sort(a+i-1,a+num);
int t=a[i]+a[i-1];
sum+=t;
a[i]=t;
i++;
}
cout<<sum;
return 0;
}
prim算法
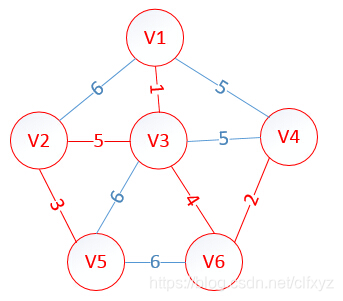
大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V
Prim算法适用于稠密图 Kruskal适用于稀疏图
初始状态：
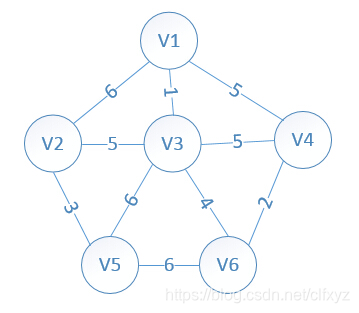
设置2个数据结构：
**lowcost[i]**表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
**mst[i]**表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST
我们假设V1是起始点，进行初始化（代表无限大，即无通路）：
lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=，lowcost[6]=*
mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）
明显看出，以V3为终点的边的权值最小=1，所以边<mst[3],3>=1加入MST
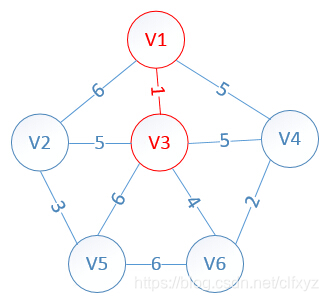
此时，因为点V3的加入，需要更新lowcost数组和mst数组：
lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4
mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3
明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST
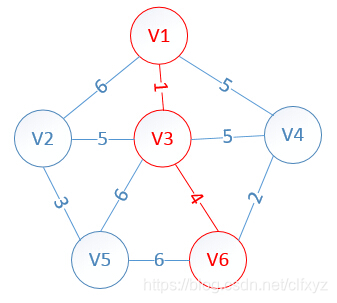
此时，因为点V6的加入，需要更新lowcost数组和mst数组：
lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0
mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0
明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST
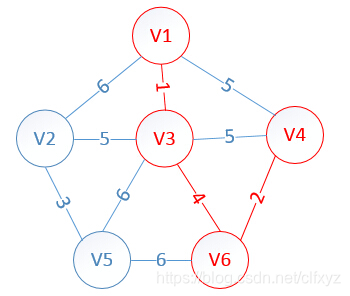
以此类推，至如图所示：
#include<bits/stdc++.h>
using namespace std;
int V,E; //V:节点数 E:边数
float a[100][100]; //二维数组a: 邻接矩阵，a[i][j]: i--j的权值
int values=0; //总权值
float lowest[100]; //lowest[i]表示以i节点作为结尾的，离大集合最近的距离
int closest[100]; //closest[i]表示以i为尾点的头点
int v[100]; //v[i]表示节点，1代表在大集合中，0代表没有
int low(float a[]){ //寻找离大集合最小权值的点
int minn=1000,j=0;
for(int i=1;i<=V;i++){
if(a[i]!=0&&a[i]<minn){ //a[i]=0时，说明此节点已经在大集合中，不再算数
minn=a[i];
j=i;
}
}
return j; //返回最小权值的点
}
void prim(){
v[1]=1;
lowest[1]=a[1][1];
for(int i=2;i<=V;i++){ //此段均是将各数组进行第一轮初始化
v[i]=0;
closest[i]=1;
lowest[i]=a[1][i];
}
for(int j=2;j<=V;j++){ //1节点已经固定，每次循环找出一个合适节点加入大集合，故循环V-1次
int k=low(lowest); //寻找权值最小的节点，并加入大集合
v[k]=1;
cout<<k<<" "<<closest[k]<<" "<<lowest[k]<<endl;
values=values+lowest[k];
lowest[k]=0; //以刚寻找到的节点为尾点的权值置0，防止干扰，相当于将此节点去掉
for(int i=1;i<=V;i++){
if(v[i]!=1&&a[k][i]<lowest[i]){ //将lowest，closest数组进行更新，进行下一轮寻找
lowest[i]=a[k][i];
closest[i]=k;
}
}
}
cout<<"最小生成树的权值为:"<<values;
}
int main(){
cin>>V>>E; //输入节点数和边数
for(int i=1;i<=V;i++){
for(int j=1;j<=V;j++){ //两个for循环用来初始化邻接矩阵数组
if(i==j) //对角线初始化为:0 其他的初始化为大数:1000
a[i][j]=0;
else
a[i][j]=1000;
}
}
int x,y;
float z;
for(int i=1;i<=E;i++){ //将邻接矩阵信息录入,没有相邻的为权值为1000，即为无穷大，无法达到
cin>>x>>y>>z;
a[x][y]=a[y][x]=z;
}
prim();
return 0;
}
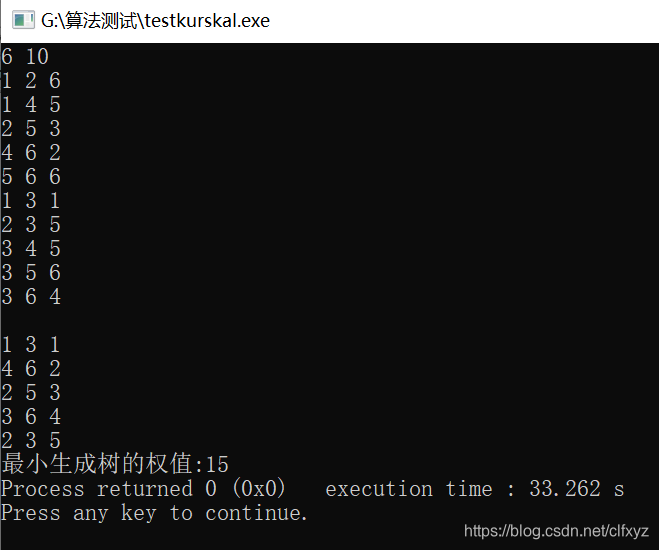
Kruskal算法：
基本思想:
各顶点各自构成一个连通分量。将边按权值由小到大排序，依次考察边集中的各条边。
（1）若被考察的两个顶点属于不同的连通分量，则将边加入到集合中，同时把两个连通分量合并为一个，继续考察下一条边；
（2）若被考察边的两个顶点属于同一个连通分量，则将边舍去，以免造成回路，继续考察下一条边。
连通分量的判断：
Kruskal算法实质上是使生成树以一种随意的方式生长，初始时每个顶点构成一棵生成树，然后每生长一次就将两棵树合并，最后合并成一棵树。
可以设置一个数组parent[n]，parent[i]表示顶点i的双亲节点。
（1）初始时，parent[i]=-1：表示顶点i没有双亲，即该节点是所在生成树的根节点；
（2）对于边（u,v），设v1和v2分别表示两个顶点所在树的根节点，如果v1!=v2，则顶点u、v必在不同的连通分量，令parent[v2]=v1，实现将两棵树的合并。
（3）求顶点v所在生成树的根节点只需沿数组v=parent[v]，不断查找v的双亲节点，直到parent[v]=-1.
#include<bits/stdc++.h>
using namespace std;
int num=0;
int values=0;
struct node{ //struct:结构, 封装node节点
int v1,v2;
float w;
};
int findroot(int parent[], int v){ //查找节点v的根节点
while(parent[v]!=-1){ //当v的parent节点为-1，说明已经找到
v=parent[v]; //否则一直找其父节点，直到为-1
}
return v;
}
void kruskal(node a[], int V, int E){
int parent[V+1]; //定义parent[]数组，parent[i]代表节点i的双亲
for(int i=1;i<=V;i++){
parent[i]=-1; //将所有节点双亲初始化为-1，意为所有节点均没有父节点，自己为一个连通分量
}
for(int i=1;i<=E;i++){ //将所有排好序的边依次查找一次
int p1=findroot(parent,a[i].v1); //查找边左节点的父节点
int p2=findroot(parent,a[i].v2); //查找边右节点的父节点
if(p1!=p2){ //两者不相同说明不在同一个连通分量，可以合并成一个
cout<<a[i].v1<<" "<<a[i].v2<<" "<<a[i].w<<endl;
values=values+a[i].w;
parent[p2]=p1; //合并两个，形成新的父节点
num++; //num进行计数
if(num==V-1){ //当总加入的边数=节点数-1时，代表最小生成树已经完成
cout<<"最小生成树的权值:"<<values;
return;
}
}
}
}
int main(){
int V,E; //V:顶点数 E:边数，录入
cin>>V>>E;
node a[E+1]; //定义一个数组，数组每个元素是节点，节点里有封装有不同的值
for(int i=1;i<=E;i++){
cin>>a[i].v1>>a[i].v2>>a[i].w; //依次将节点元素值录入
}
cout<<endl;
node t;
for(int i=0;i<E-1;i++){ //利用冒泡排序，将封装好的节点按节点里a[i].w元素值的大小进行排序
for(int j=1;j<E-i;j++){
if(a[j].w>a[j+1].w){
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
kruskal(a,V,E); //调用kruskal算法生成最小生成树
return 0;
}
扫一扫
1478
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
