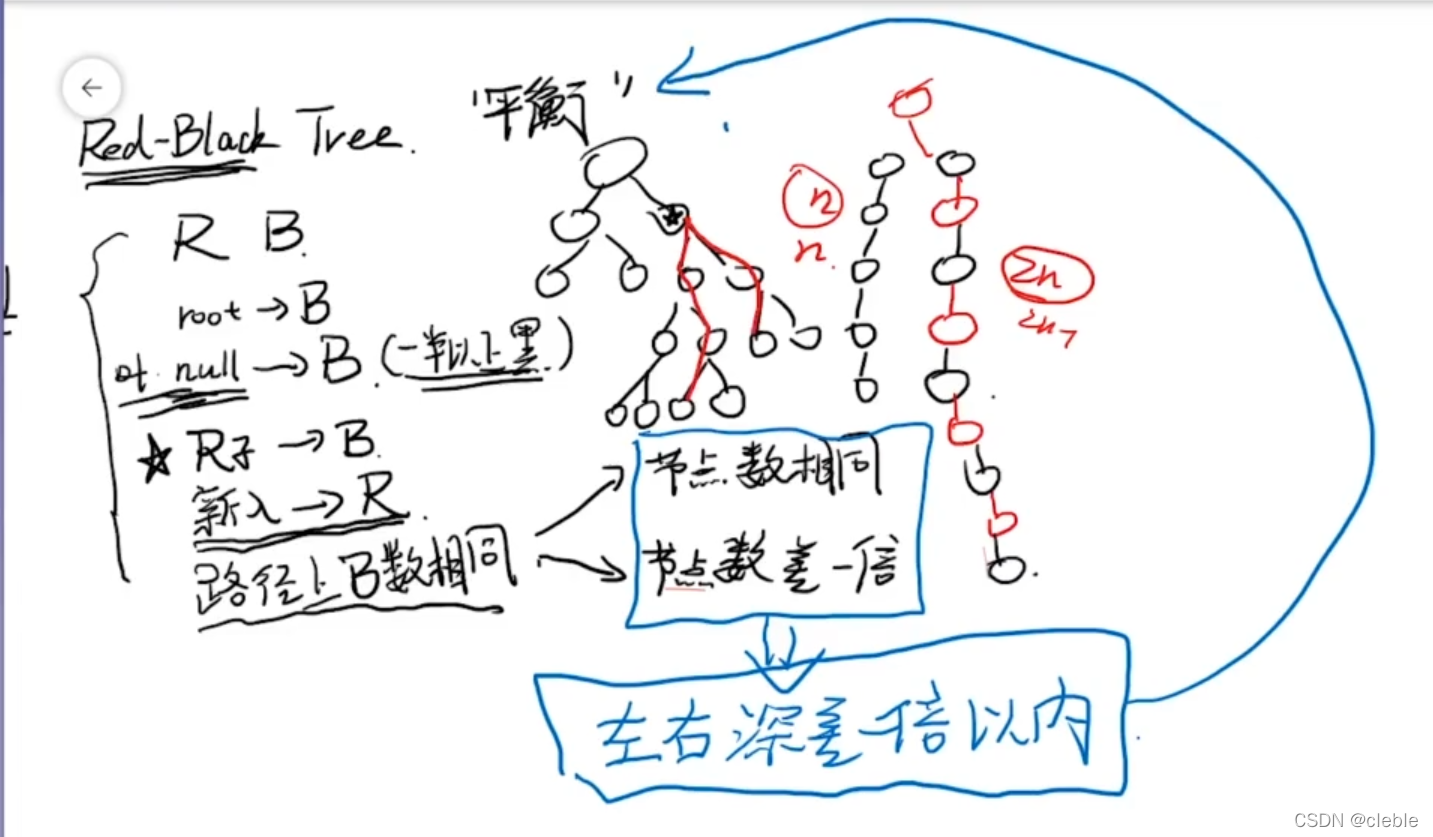
AVL树左右深差1(平衡条件太严格了,实际中很少符合),而红黑树左右深差1倍以内(平衡条件比较宽松,实际中经常用到),导致红黑树写的性能更高一些。 BST:数据递增或者递减的时候,就退化成了链表。
BST:数据递增或者递减的时候,就退化成了链表。
AVL:平衡条件太严格了。时间复杂度的是LogN。
Red-Black Tree:平衡条件比较宽松,新增节点的时候带来的树的操作的变动小很多。时间复杂度的是LogN。
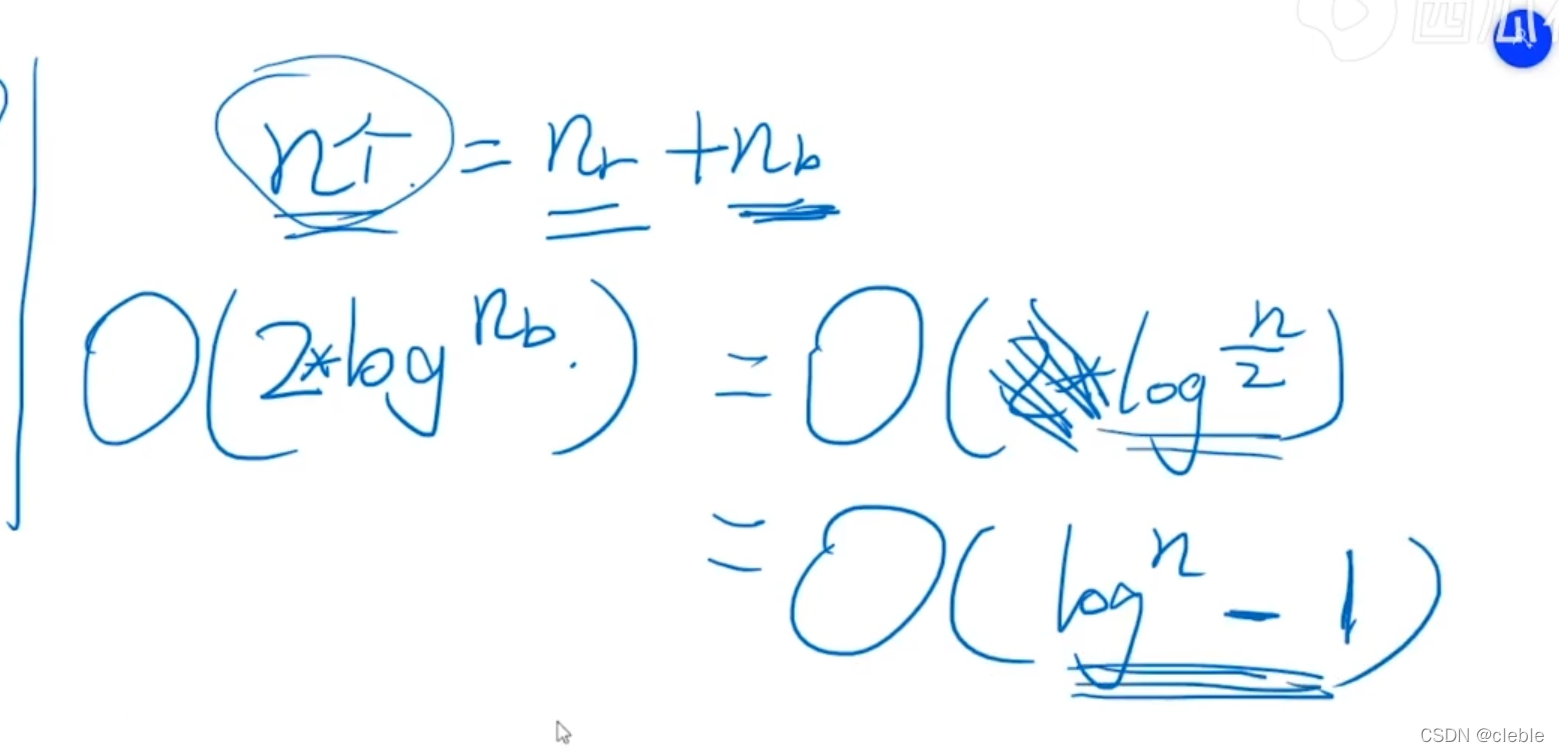
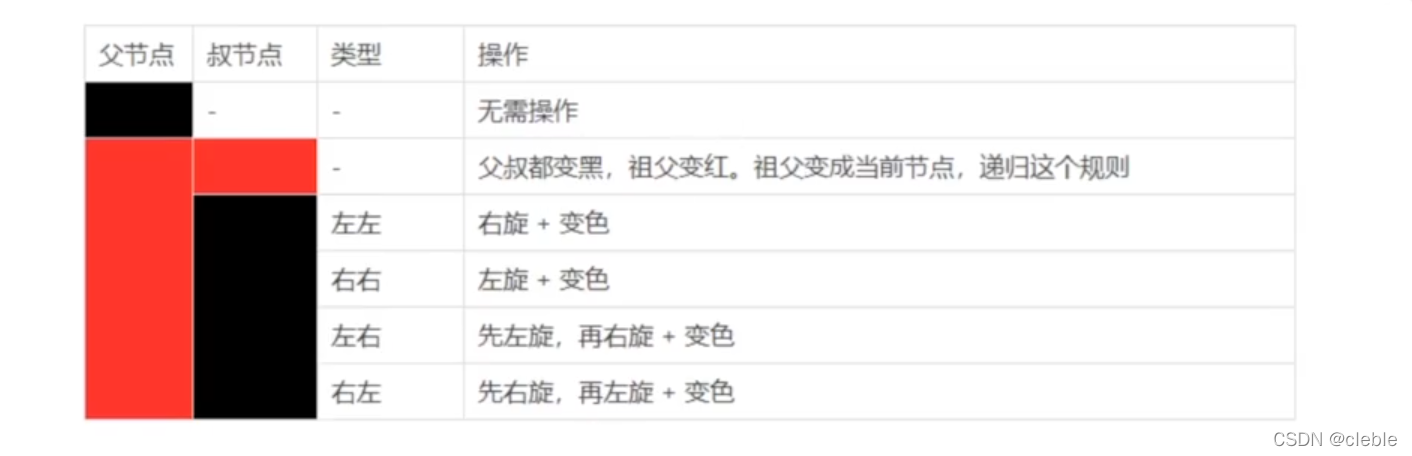
 本文探讨了红黑树和AVL树的区别,指出AVL树由于严格的平衡条件导致其在实际应用中不如红黑树常见。红黑树允许左右子树深度差一倍以内,因此插入操作带来的树结构调整较小,时间复杂度仍为LogN,这使得红黑树在性能上更为优越。同时,AVL树在数据递增或递减时可能退化成链表,效率降低。
本文探讨了红黑树和AVL树的区别,指出AVL树由于严格的平衡条件导致其在实际应用中不如红黑树常见。红黑树允许左右子树深度差一倍以内,因此插入操作带来的树结构调整较小,时间复杂度仍为LogN,这使得红黑树在性能上更为优越。同时,AVL树在数据递增或递减时可能退化成链表,效率降低。

AVL树左右深差1(平衡条件太严格了,实际中很少符合),而红黑树左右深差1倍以内(平衡条件比较宽松,实际中经常用到),导致红黑树写的性能更高一些。 BST:数据递增或者递减的时候,就退化成了链表。
BST:数据递增或者递减的时候,就退化成了链表。
AVL:平衡条件太严格了。时间复杂度的是LogN。
Red-Black Tree:平衡条件比较宽松,新增节点的时候带来的树的操作的变动小很多。时间复杂度的是LogN。


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


