论文研读_一种基于双重分解和子集选择的多模态多目标进化算法（MMOEA/DS2）精简版

论文研读_一种基于双重分解和子集选择的多模态多目标进化算法（MMOEA/DS2）

• 此篇文章为A multi-modal multi-objective evolutionary algorithm based on dual
  decomposition and subset selection的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正!

算法

本节介绍了我们提出的算法 MMOEA/DS2。首先概述了算法的总体框架，随后详细描述了主要组成部分。

1 总体框架

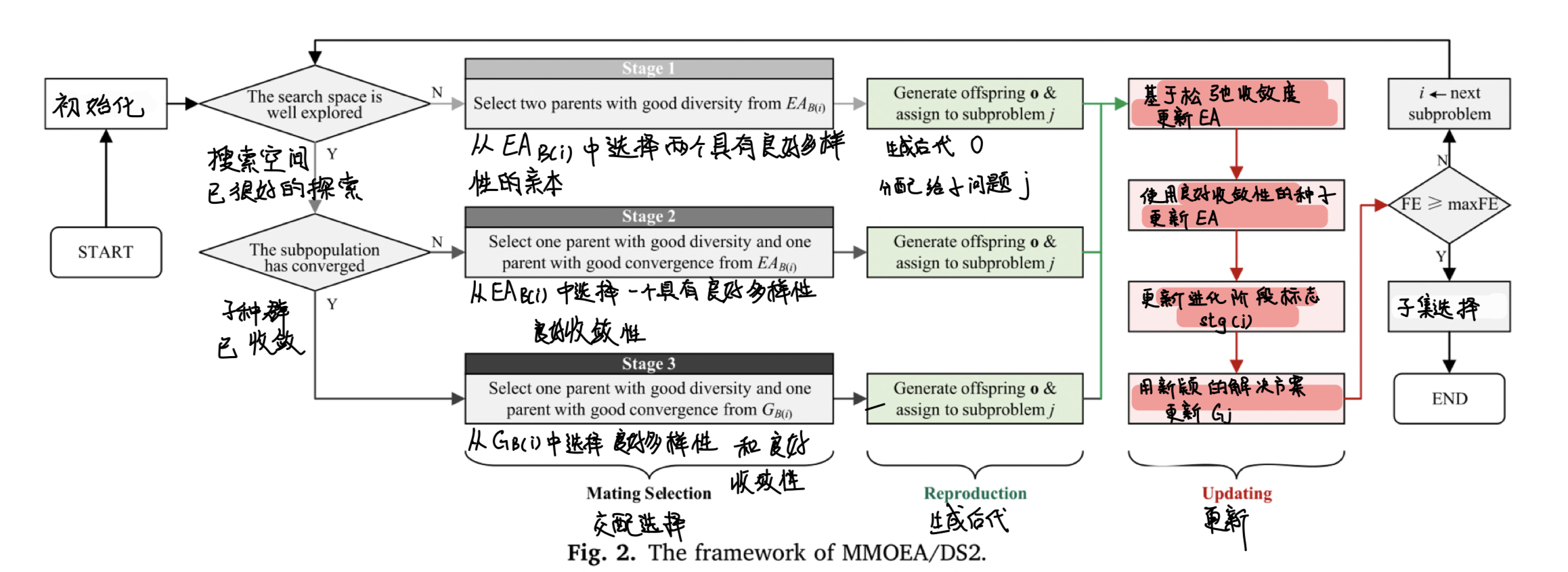
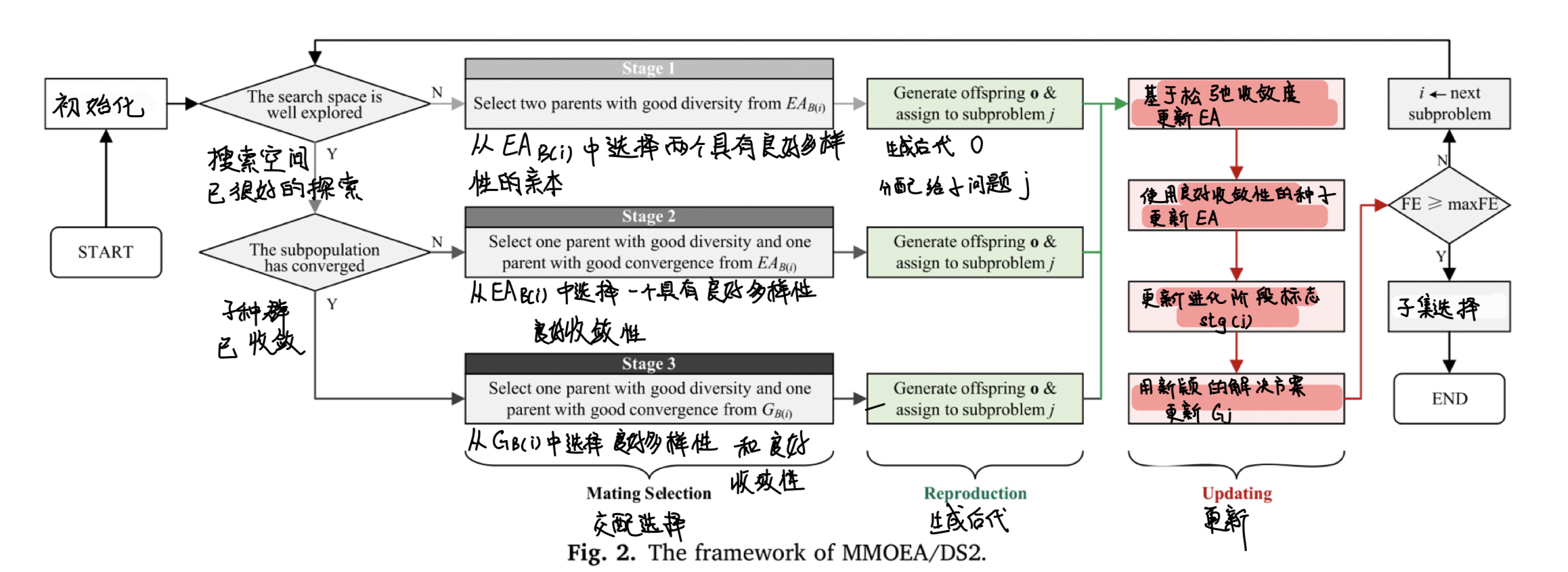
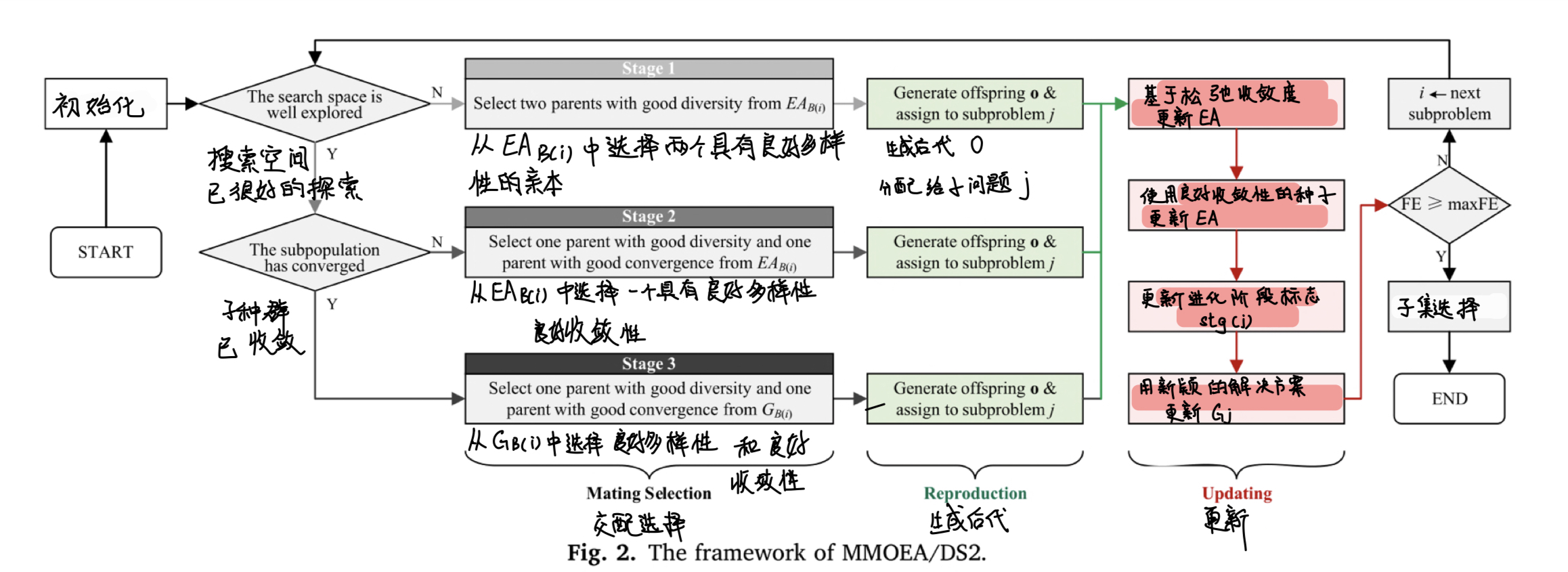
如图2所示，所提出的 MMOEA/DS2 算法通过网格 G 和外部存档 EA 的合作解决问题。具体来说：

• 网格 G ，用于保留新颖的高性能解决方案，作为定位不同 PSs 的优化器；
• 外部存档 EA ，用于存储在演化过程中发现的所有有前景的解决方案，作为历史有希望位置的记忆和当前演化状态的检测器。

MMOEA/DS2 的框架在算法 1 中描述。

在初始化阶段，生成一组均匀分布的权重向量 $\Lambda ={\lambda }_1,{\lambda }_2,...,{\lambda }_N$ 和网格 G = {g₁ , g₂ ,…, g_Ng } ，其中 λ_i 和 g_s 分别决定第 i 个子问题 f_i 和第 s 个子区域。然后，为每个子问题 f_i 确定邻域 B(i) ，以限制交配和更新。初始种群 P₀ 随机生成以初始化理想点 z*、网格 G 和外部存档 EA 。
接下来，在主循环中， MMOEA/DS2 限制在邻域 $B(i)$ 内的交配，并根据当前 $f_i$ 的优化状态自适应地选择两个父代。

• 具体来说，如果识别出新的多样性种子并加入到 $E{A}_i$ 中，这意味着搜索空间还没有被充分探索，此时会选择两个具有良好多样性的亲本。

• 否则，如果历史上最好的收敛程度更新了，我们认为子种群尚未收敛到 PF ，因此分别从具有良好收敛性和良好多样性的父代中选择一个。否则， f_i 的有前景位置应该已被充分探索，两个父代将从 G_B(i) 而非 EA_B(i) 中选出，以避免陷入局部最优。在通过繁殖操作产生后代 o 后，根据到每个权重向量的最短垂直距离，将其分配给子问题 $f_j$ 。之后，MMOEADS2 检查是否更新外部存档 $E{A}_j$ 、阶段标志 stg(j) 和网格 G_j 。主循环将重复进行，直到耗尽最大函数评估次数。最后，我们执行子集选择操作以截断 EA 并获得大小为 N 的最终解决方案集 S 。

2 自适应多阶段交配选择

交配选择的理念仍然使用与 MOEA/D [4] 中相同的邻域交配限制方案，以实现均匀探索，即在每个子问题的邻域内交配，以更高的概率在未探索的子区域产生后代。采用锦标赛选择方法从交配池中选择两个父代。交配池的构建及选择标准会根据子问题当前的优化状态自适应变化。

根据当前阶段 $stg$ 来进行交配选择

通过算法4

• EA $d_j$通过新的多样性种子更新，这表明存在潜在的等效PS需要探索。因此，将stg(j)设为1，并选择具有更好多样性的解作为其中一个亲本，以增强种群多样性；

• hb $j$ 通过在子问题 $f_j$ 上具有更好收敛度的更新，这意味着种群尚未收敛到PF。因此，将stg(j)设为2，在交配选择中，将优先考虑具有更好收敛度的解；

• 否则，搜索只需进一步开展，以更好地逼近等效PSs。并且stg(j)被标记为3。

如算法 2 所示，如果阶段等于 1 ，搜索空间仍需探索，因此优先选择具有良好多样性的解。那些被分配到 EA_B(i) 并且多样性程度被调整的解，构成了第一个交配池 pool₁ 和选择标准 crt₁（第 2-3 行）。然后，从 pool₁ 中随机选择两个解 x₁ 和 x₂ 。

1. 随机选择两个解决方案（x1和x2）

2. 选择标准确定（Criterion Determination）

   • 步骤2至8：这个部分基于输入的**选择标准（crt）**来确定比较的依据。
     • 如果选择标准是多样性（Div），则计算每个解的多样性程度（步骤3），并以 负多样性值 作为比较标准（步骤4），即选择 多样性较低 的解。
     • 如果选择标准是收敛性（Con），则计算每个解的收敛程度（步骤6），并以 收敛性值 作为比较标准（步骤7），即选择 收敛性更好 的解。

   选择多样性较低的解主要是为了探索解空间中的特定区域，而选择收敛性更好的解则是为了尽快找到最优解。

3. 比较和选择（Comparison and Selection）

• 步骤9至13：这个部分涉及比较两个解决方案（ x1 和 x2 ）基于之前确定的标准（ 多样性 或 收敛性 ）。根据比较结果，选择更优的解作为亲本解（parent solution）。

选择第一个标准值更好的解，如算法 3 中所做的那样，作为第一个父代 p₁ 。对于 p₂ ，如图 3 所示，选择两个多样性程度较高的父代（例如， p₁ 和 x₃ ）会增加在远离可能的 PSs 的子区域内产生后代的机会。因此，我们进一步限制 p₂ 的选择范围，在 p₁ 的 K 个最近邻居内选择（第 5 行），以产生高质量的后代。

如果阶段等于 2 ，交配选择将考虑解的收敛性，因此收敛程度被用来确定第一个父代 p₁ （第10行）。

然后，根据多样性程度从 EA_B(i) 中选择第二个父代 p₂ （第12-13行）。第二个交配池 pool₂ 由 EA_B(i) 填充，而不是 p₁ 的邻居，以避免对早期获得的 PSs 进行偏向性搜索。

对于阶段 3 ， EA_B(i) 中的解应该已经充分探索了子问题 f_i 的搜索空间。并且所有历史搜索信息已由网格 G_B(i) 收集。因此，阶段 3 的父代选择是在 G_B(i) 的单元格内进行的，这被构建为一个多臂老虎机选择问题。具体来说，我们利用上置信界限（UCB）函数来驱动选择过程[35]：

其中 $N_s$ 是每个子问题的选择总次数， $n(g)$ 表示网格 g 被选择的次数；而 $w(g)$ 显示了相应的奖励，

如公式 (5) 所示， $w(g)$ 不依赖于适应度，而是奖励那些产生能够存活下来的后代的单元格。因此，对于子问题产生有希望的后代的单元格将有更高的机会被选为第一个交配池 pool₁ 。同时，每个解的收敛程度被作为第一个标准进行调整，以避免产生收敛性差的 PF 后代。之后，选择 p₁ 的K个最近邻居作为 pool₂ ，以更好地开发邻域区域并微调种群。从 pool₂ 中随机选择的两个解中，多样性程度更好的解被调整为 p₂ 。

3 基于双重分解的分配

在配对选择中确定了两个亲本之后， MMOEA/DS2 利用遗传算法操作符（即 SBX 交叉和多项式变异[36]）来生成后代解 o 。然后，我们基于双重分解将 o 分配给子问题，旨在促进目标空间和决策空间的多样性。主要步骤如下：

1) 基于权重向量和网格的双重分解

在初始化阶段，首先使用 Das 和 Dennis 的 [37] 系统方法生成一组均匀分布的权重向量 Λ = { λ 1 , λ 2 , . . . , λ N } \Lambda = \{\lambda_1, \lambda_2, ..., \lambda_N\} Λ={λ1​,λ2​,...,λN​} ，就像在大多数MOEA/D类型算法[4]中所做的那样。然后，将 Nd 维决策空间的每个维度离散化为 nk 个连续段，其中 $nk=\lceil \sqrt{\frac{N\cdot M}{2}}\rceil$ ， N 和 M 分别表示种群大小和目标数量。在第 d 维中，每个段的宽度 $l_d$ 是通过以下方式计算的，

其中 $x_{d_u}$ 和 $x_{d_l}$ 分别是决策空间中第 d 维的上界和下界。因此，整个决策空间，记为 $\Omega ={\prod }_{d=1}^{N_d}[x_{d_l},x_{d_u}]$ ，被划分为 $n{k}^{N_d}$ 个正交网格单元。为了避免网格大小的指数增长和减轻计算负担，当 $N_d>3$ 时，我们随机选择三个维度进行划分。

2) 分配给子问题

然后，后代解 o 根据与 ${\lambda }_j$ 之间的最小垂直距离，被分配给第 j 个子问题。

其中 $Co{n}_k(x)$ 是解 x 在子问题 $f_k$ 上的收敛程度。

如图 4 (a) 所示，后代被分配给 $f_3$ ，更新仅发生在分配给 $f_3$ 的解内。对于$f_3$，只有被分配给$f_3$的解会被新的后代所更新。在 MMOEA/DS2 中，解之间的竞争被限制在子问题内部，这在保持目标空间多样性方面起着重要作用。
在这张图中，我们也可以看到一个理想点 $z^{\ast }$ ，它通常代表目标空间中的一个理论上的最优点，在实际应用中，这个点可能是不可达的，但它提供了一个方向或参考，让算法知道如何引导解的搜索过程。此外，通过向量 $\lambda$ 表示的方向有助于定义在目标空间中导向不同区域的偏好方向

3) 分配给网格单元

随后，后代进一步被分配到网格中，用于收集每个子问题的搜索空间信息。解 x 在网格 G 中所处的单元格索引号是根据其坐标位置确定的：

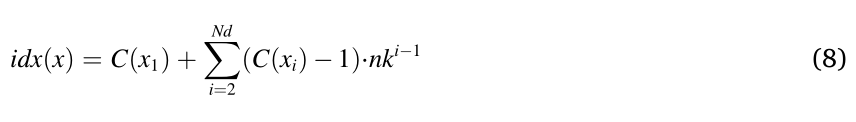
其中 $n_k$ 是每个维度中的分段数； $C(x_i)$ 表示解 x 在第 i 维的坐标，可通过以下方式计算：

其中 $x_i^l$ 和 $l_i$ 是决策空间中第 i 维的下界和网格宽度。

图 4 (b) 展示了一个示例，进一步将后代 o 分配给子问题 $f_3$ 的网格。这个例子中的搜索空间是 $\Omega =[0,10]\times [0,10]$ ，并且每个维度被划分为十个部分，即 $n_k=10$ 。然后，两个维度中每个段的宽度都是 1 。假设后代 o 的决策变量是 [6.4, 1.7] ，那么 o 的坐标可以通过 $C(x_1)=\lfloor (6.4-0)/1\rfloor +1=7$ 和 $C(x_2)=\lfloor (1.7-0)/1\rfloor +1=2$ 来获得。接着，后代 o 将被分配到的网格单元的索引号由 $idx(o)=7+(2-1)\cdot 10=17$ 给出。

4) 更新网格单元

接下来，后代 o 将与被分配到的网格单元中的当前解合并。如果满足以下条件之一，网格单元将会被更新：

• 如果解的数量小于网格密度，所有解都将被保留；
• 如果解的数量超过网格密度，那么适应性最差的解将被删除。

第一个条件表明后代 o 到达了一个尚待探索的区域，而第二个条件意味着后代找到了一个性能更高的位置。换句话说，每个网格单元只保留到目前为止在该区域找到的新颖且性能高的解。网格密度被调整以限制每个网格中存储的解的规模。

如图 4 (b) 所示，索引为17的网格单元的解是 x₁ 、 x₂ 和 o 。如果网格密度设置为 4 ，则后代 o 将直接被保留。如果网格密度设置为 2 ，则会删除收敛度最差的解（即 x₁ ）。在这篇论文中，网格密度被设置为 Nd+1 。

4 更新外部存档

在 MMOEA/DS2 中，使用一个外部存档来维护有前景的解，并评估每个子问题的当前优化状态。外部存档 EA 由历史最佳解 hb 、基于收敛度的外部存档 $E{A}_c$ 和以多样性为导向的外部存档 $E{A}_d$ 组成。

1. 输入和输出：
   • 输入包括外部存档（$EA$）、子问题（$f_j$）、当前优化状态标志（$stg(j)$）、后代（$o$）、当前代数（$gen$）和最大接受阈值（ ${\epsilon }_{m}ax$ ）。
   • 输出为更新后的外部存档（$EA$）和当前优化状态标志（$stg(j)$）。
2. 基于松弛收敛度更新EA：
   • 第2行：更新历史最佳收敛度（$h{b}_j$）为后代o的收敛度。
   • 第3行：根据收敛度和 ${\epsilon }_{m}ax$ 更新EA的收敛部分（ $E{A}_c^j$ ）。
3. 使用多样性种子更新EA：
   • 第5行：根据当前代数和总代数更新松弛阈值（ $\epsilon$ ）。
   • 第6行：根据 多样性种子 更新 EA 的多样性部分（ $E{A}_d^j$ ）。
   • 第7-9行：如果 $E{A}_d^j$ 的大小超过了某个阈值 $Ns$ ，进行多样性种子检测并相应更新 $E{A}_d^j$ 。
4. 更新优化状态标志stg(j)和$G_j$

如算法 4 所述，更新每个子问题的 EA 包括三个关键程序：基于放松收敛度的更新、以多样性增强为导向的更新和当前优化状态检测。
首先， MMOEA/DS2 检测生成的后代 o 是否通过方程式 (3) 更新了子问题 $f_j$ 上的历史最佳收敛度 $h{b}_j$ 。然后，基于收敛度的 $E{A}_c^j$ 与 o 结合并通过放松收敛度进行更新，更新后的 $E{A}_c^j$ 满足 $Con(E{A}_c^j)\le Con(h{b}_j)\cdot (1+{\epsilon }_{m}ax)$ 。
接下来，MMOEA/DS2 检测那些有潜力增强决策空间种群多样性的种子解。种子多样性的检测基于这样一个假设：靠近等效 PS 的解具有相对较好的收敛度。并且，候选 EA_d_j 的收敛度接受阈值通过以下方式更新：

其中 $gen$ 和 $Gen$ 分别是 当前迭代次数 和 最大迭代次数 。类似于选择 $E{A}_c^j$ ， $E{A}_d^j$ 与 o 结合并通过更放松的收敛度更新，候选 $E{A}_d^j$ 满足 $Con(E{A}_d^j)\le Con(h{b}_j)\cdot (1+{\epsilon }_c)$ 。为了避免影响解的整体收敛性，候选 $E{A}_d^j$ 被截断为 $2\ast Nd$ 个解，这些解是决策空间距离 $h{b}_j$ 对应解最远的解。
接着，基于 $E{A}_j$ 的更新状态评估当前子问题 $f_j$ 的优化状态。具体来说，优化状态被分为以下三种情况：

• $E{A}_d^j$ 使用新的多样性种子进行更新，这表明存在潜在的等效 PS（Pareto解集）需要探索。因此，stg(j)被设为1，而具有更优多样性的解被选为亲本之一，以此提升种群的多样性。
• 在子问题 $f_j$ 上， $h{b}_j$ 更新为具有更好收敛度的解，这意味着种群尚未收敛至 PF（Pareto前沿）。因此， stg(j) 被设为 2 ，在配对选择过程中，将优先考虑具有更好收敛度的解。
• 否则，搜索仅需进一步深入，以更好地逼近等效 PS（Pareto解集）。于是， stg(j) 的值被设定为 3 。

图 5 展示了在不同搜索阶段，两个档案解在决策空间中的分布情况。首先，这两个档案都是通过随机生成的初始种群进行初始化，它们在决策空间中分布广泛。在早期阶段，由于收敛度更好， $E{A}_c$ 的解在 $P{S}_1$ 附近更密集。同时，后代 o 被接受为多样性种子，采用更宽松的收敛度，以探索潜在的 PS 。因此，从 o 和 $x_2$ 生成接近 $P{S}_2$ 的后代是有希望的。此外，允许具有较差收敛度的解（例如， $x_1$ ）反过来可能降低搜索效率。这就是我们限制 $E{A}_d$ 大小并随着搜索进展减小 ${\epsilon }_c$ 的原因。
在中期阶段， $E{A}_c$ 通过更新每个子问题上的历史最佳收敛度，收集了更接近 PS 的解。另一方面， $E{A}_d$ 中的多样性种子避免了搜索陷入收敛度最佳的 PS 。在最后阶段， $E{A}_c$ 收集的解已经识别并定位了具有良好收敛度和分布的不同PS。

1. 初始阶段：
   • 档案初始化：两个档案，$E{A}_c$ 和 $E{A}_d$，最初通过随机生成的初始种群初始化，在决策空间中分布广泛。
   • $E{A}_c$的特点：$E{A}_c$ 更倾向于收敛性好的解，所以它的解在决策空间的特定区域（$P{S}_1$）中更密集。
   • 多样性探索：后代o被作为多样性种子接受，用较宽松的收敛度探索其他潜在的优化解（Pareto Set, PS）。这意味着生成接近另一个潜在优化解集合（$P{S}_2$）的后代是可行的。
2. 中期阶段：
   • $E{A}_c$的更新：$E{A}_c$通过更新每个子问题上的历史最佳收敛度，收集了更接近PS的解。
   • $E{A}_d$的角色：$E{A}_d$中的多样性种子帮助避免搜索过程只集中在收敛度最佳的PS，从而维持搜索的多样性。
3. 后期阶段：
   • $E{A}_c$的收集结果：此时，$E{A}_c$已经收集到了一些既有良好收敛度又分布良好的解，这些解能够识别并定位不同的PS。
     此外，文中还提到了一些操作策略，例如限制$E{A}_d$的大小并随着搜索进展减小${\epsilon }_c$。这些策略的目的是为了平衡收敛性和多样性，确保算法能有效地探索决策空间并识别出优质解。
     总的来说，这段话说明了在多目标优化中，如何通过不同的档案管理策略来平衡解的收敛性和多样性，以及这些策略如何随着搜索阶段的变化而调整。

5 基于外部档案的最终子集选择

当满足停止准则时，算法停止并输出最终解集。尽管 $E{A}_c$ 中的最终解在目标和决策空间都保持了良好的收敛度和多样性，但其大小远大于种群规模 $N$ 。此外，提供整个解集会增加决策者的选择负担。因此，执行最终子集选择程序，以选出代表性解，并输出一个大小为 N 的解集，这些解集对 $PF$ 和 $PS$ 具有良好的逼近度。

算法 5 展示了最终子集选择策略的细节。首先，将为每个子问题收集的所有档案解合并，并剔除重复的解。然后，使用分布均匀的权重向量依次选择候选解集 $S_C$ 。

图 6 展示了最终子集选择的一个示例，其中选中的解、候选解和档案解分别以红色、蓝色和白色显示。对于当前的权重向量 ${\lambda }_j$ ，最佳收敛度 $Co{n}_b$ 通过方程 (3) 获得。根据 MMOPs 的定义， $E{A}_C$ 拥有多个满足 $Co{n}_j(S_C)\le Co{n}_b(1+{\epsilon }_{m}ax)$ 的解。

如图 6 所示，候选解 $x_a$ 和 $x_b$ 都对 ${\lambda }_j$ 有着有希望的收敛度。被选中的解将是对已选解集（即 S ）多样性度最大的解。因此，解 $x_b$ 被选择加入到 S 中。总而言之，均匀分布的权重向量和基于收敛度的候选集构建保证了目标空间的收敛度和多样性，而基于多样性度的最终解选择强调了决策空间的多样性。