HBU深度学习实验9-前馈神经网络（5）

一、梯度下降法

参考链接：

梯度下降（一）：批梯度下降、随机梯度下降、小批量梯度下降、动量梯度下降、Nesterov加速梯度下降法 Matlab 可视化实现_动量梯度下降算法公式-优快云博客

1、批量梯度下降

根据整个数据集求取损失函数的梯度，来更新参数θ的值。

优点：考虑到了全局数据，更新稳定，震荡小，每次更新都会朝着正确的方向。
缺点：如果数据集比较大，会造成大量时间和空间开销。

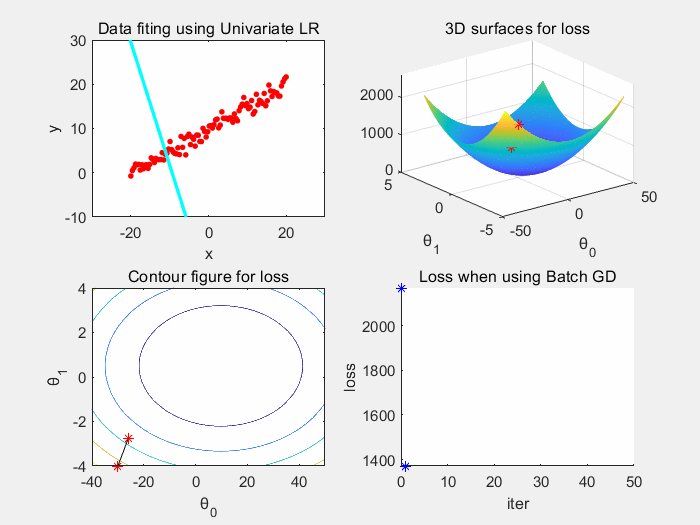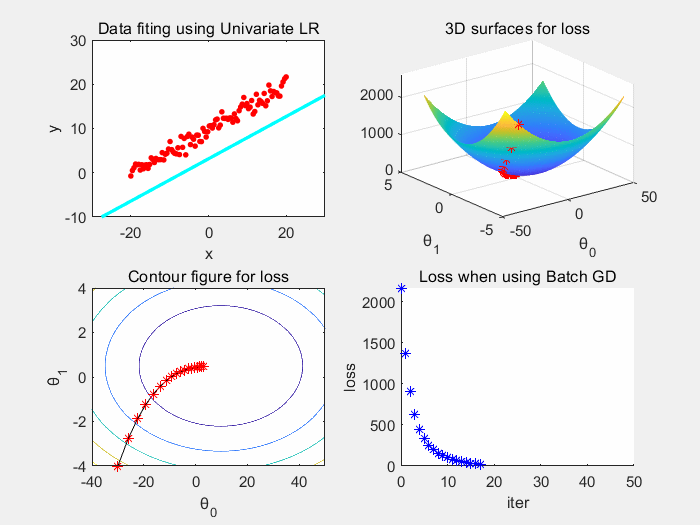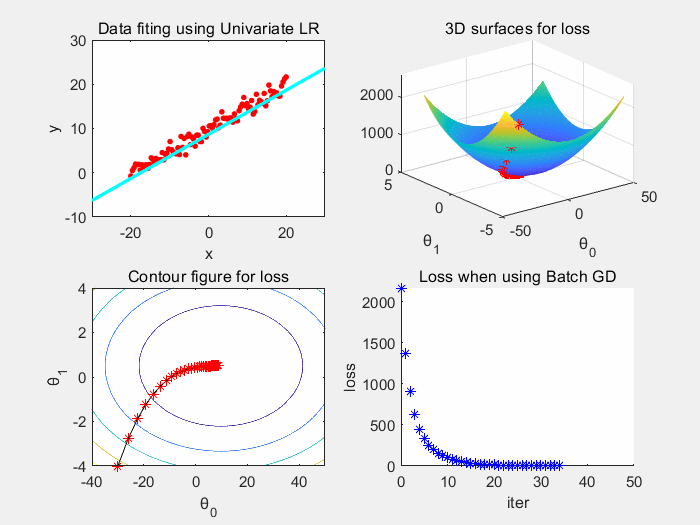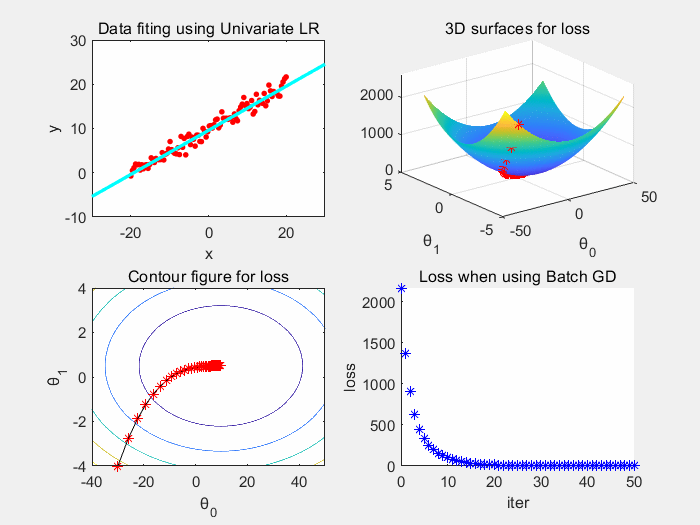
根据上图可以看到，批梯度下降收敛稳定，震荡小。 

2、随机梯度下降

因为批梯度下降所需要的时间空间成本大，我们考虑随机抽取一个样本来获取梯度，更新参数 θ

随机打乱数据集。
对于每个样本点，依次迭代更新参数θ 。
重复以上步骤直至损失足够小或到达迭代阈值。

优点：训练速度快，每次迭代只需要一个样本，相对于批梯度下降，总时间、空间开销小。
缺点：噪声大导致高方差。导致每次迭代并不一定朝着最优解收敛，震荡大。

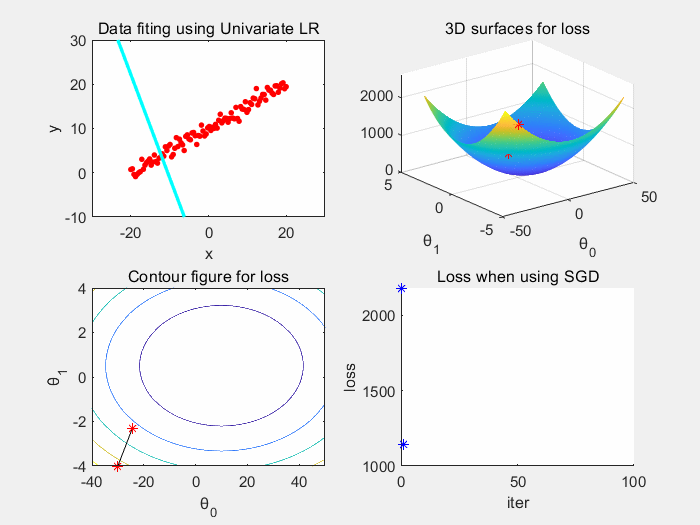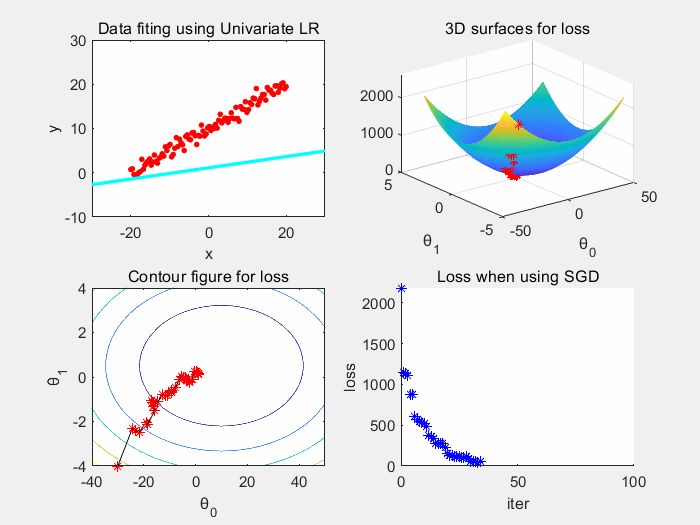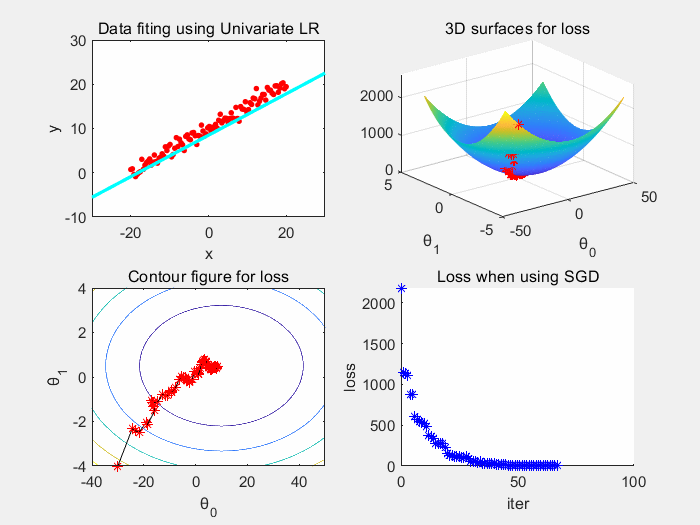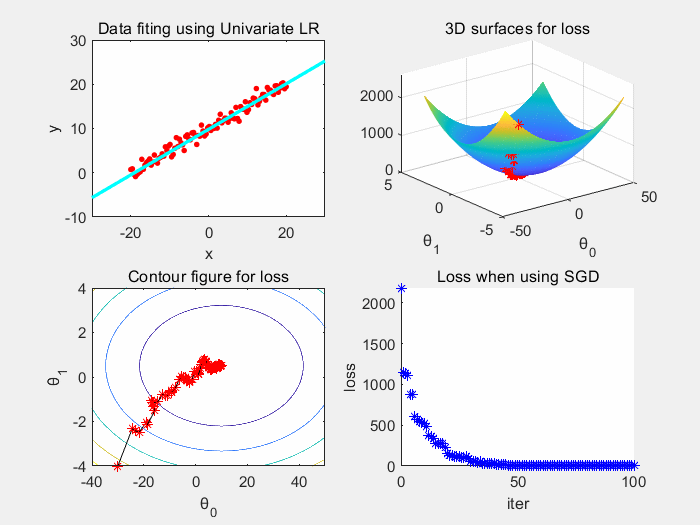
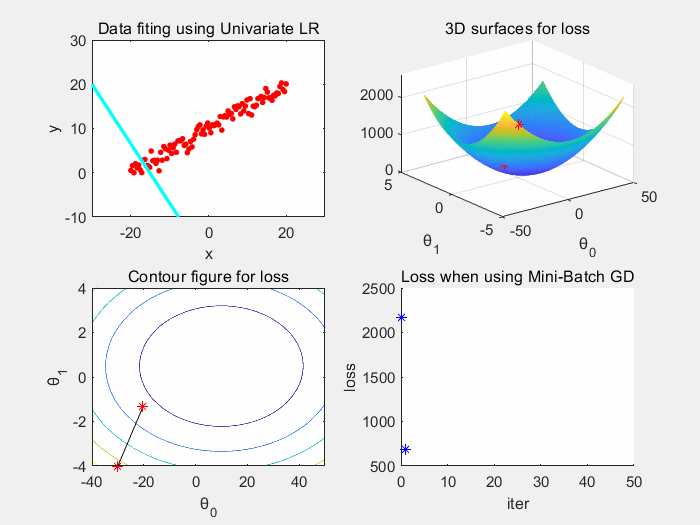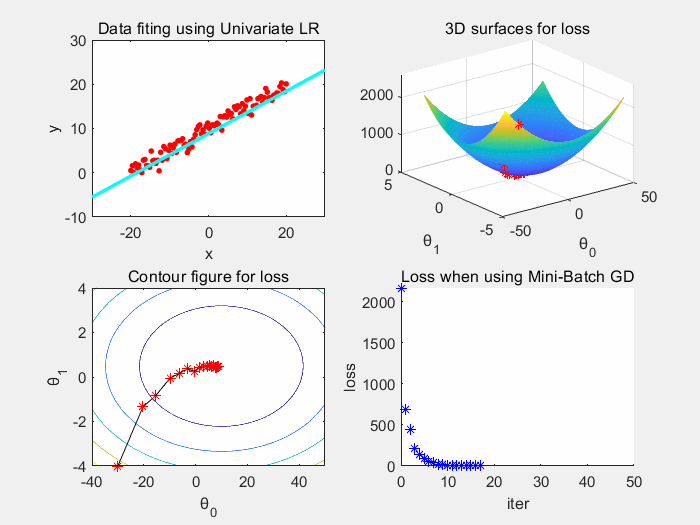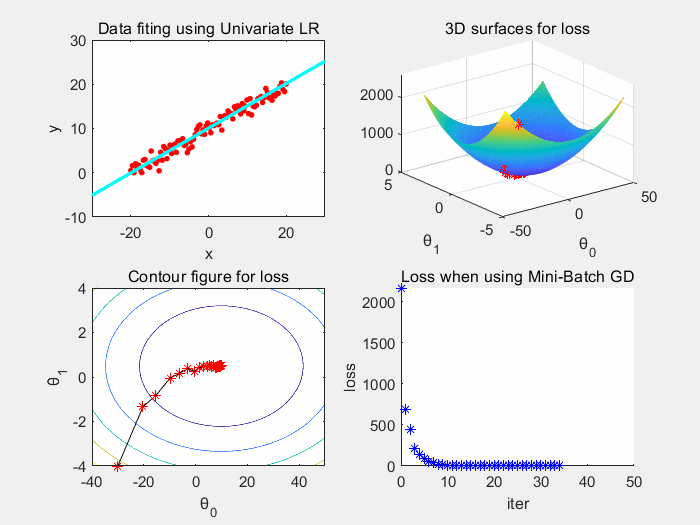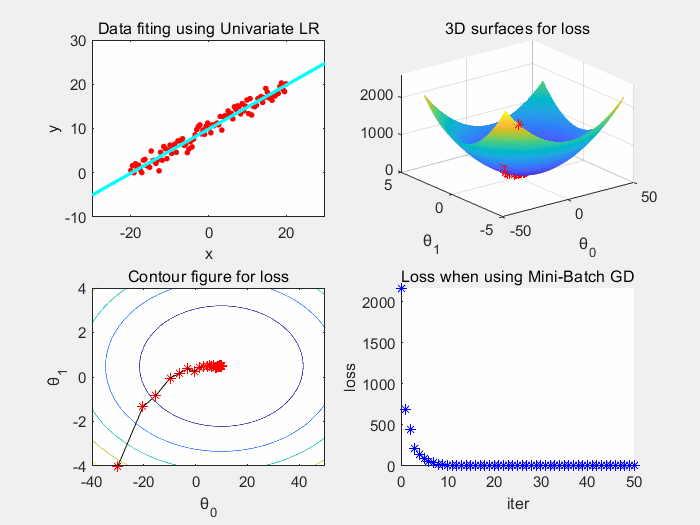
3、小批量梯度下降

随机梯度下降收敛速度快，但是波动较大，在最优解处出现波动很难判断其是否收敛到一个合理的值。而批梯度下降稳定但是时空开销很大，针对于这种情况，我们引入小批量梯度下降对二者进行折衷，在每轮迭代过程中使用n个样本来训练参数：

步骤如下：

随机打乱数据集。
将数据集分为m /n个集合，如果有余，将剩余样本单独作为一个集合。
依次对于这些集合做批梯度下降，更新参数θ 。
重复上述步骤，直至损失足够小或达到迭代阈值。

二、基于前馈神经网络完成鸢尾花分类

 完整代码

import torch.utils.data as Data
import numpy as np
import torch
import torch.nn as nn
import torch.optim as opt
import torch.nn.functional as F
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris



# 加载数据集
def load_data(shuffle=True):
    """
    加载鸢尾花数据
    输入：
        - shuffle：是否打乱数据，数据类型为bool
    输出：
        - X：特征数据，shape=[150, 4]
        - y：标签数据，shape=[150]
    """
    # 加载原始数据
    iris = load_iris()
    X = np.array(iris.data, dtype=np.float32)
    y = np.array(iris.target, dtype=np.int32)

    # 转换为PyTorch张量
    X = torch.tensor(X)
    y = torch.tensor(y)

    # 数据归一化
    X_min = torch.min(X, dim=0).values
    X_max = torch.max(X, dim=0).values
    X = (X - X_min) / (X_max - X_min)

    # 如果shuffle为True，随机打乱数据
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]

    return X, y

class IrisDataset(Data.Dataset):
    def __init__(self, mode='train', num_train=120, num_dev=15):
        super(IrisDataset, self).__init__()
        # 调用第三章中的数据读取函数，其中不需要将标签转成one-hot类型
        X, y = load_data(shuffle=True)
        if mode == 'train':
            self.X, self.y = X[:num_train], y[:num_train]
        elif mode == 'dev':
            self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
        else:
            self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]

    def __getitem__(self, idx):
        return self.X[idx], self.y[idx]

    def __len__(self):
        return len(self.y)

train_dataset = IrisDataset(mode='train')
dev_dataset = IrisDataset(mode='dev')
test_dataset = IrisDataset(mode='test')

print("length of train set: ", len(train_dataset))

batch_size = 16

# 加载数据
train_loader = Data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = Data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = Data.DataLoader(test_dataset, batch_size=batch_size)


class Model_MLP_L2_V3(nn.Module):
    def __init__(self, input_size, output_size, hidden_size):
        super(Model_MLP_L2_V3, self).__init__()
        # 构建第一个全连接层
        self.fc1 = nn.Linear(input_size, hidden_size)
        # 构建第二全连接层
        self.fc2 = nn.Linear(hidden_size, output_size)
        # 定义网络使用的激活函数
        self.act = nn.Sigmoid()
        nn.init.normal_(self.fc1.weight, mean=0., std=0.01)
        nn.init.constant_(self.fc1.bias, 1.0)
        nn.init.normal_(self.fc2.weight, mean=0., std=0.01)
        nn.init.constant_(self.fc2.bias, 1.0)

    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        return outputs


fnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size=6)

class Accuracy(object):
    def __init__(self, is_logist=True):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """

        # 用于统计正确的样本个数