常规排序之冒泡、选择和插入排序

最新推荐文章于 2023-09-18 19:53:51 发布

紫陌翌晨

最新推荐文章于 2023-09-18 19:53:51 发布

阅读量192

点赞数

分类专栏：数据结构和算法文章标签：算法 python

本文链接：https://blog.youkuaiyun.com/cjw1991/article/details/117084126

版权

数据结构和算法专栏收录该内容

2 篇文章

订阅专栏

本文详细介绍了几种基本的排序和查找算法，包括线性查找、二分查找、冒泡排序、选择排序和插入排序。线性查找的时间复杂度为O(n)，二分查找为O(logn)。冒泡排序、选择排序和插入排序的时间复杂度均为O(n^2)，分别通过不断交换、选取最小值和插入操作实现排序。这些基础算法对于理解更复杂的算法有着重要的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、查找

1.1、顺序查找(Linear Search)

顺序查找也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。

时间复杂化度：O(n)

def linear_search(li, val):
    """
    线性查找，找不到返回None
    :param li: 查找的列表
    :param val: 查找的值
    :return:
    """
    for inx, v in enumerate(li):
        if v == val:
            return inx
    else:
        return

1.2、二分查找(Binary Search)

二分查找又叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

时间复杂度：O(logn)

在这里插入图片描述

def binary_search(li, val):
    """
    二分查找，找不到返回None
    :param li: 查找的列表
    :param val: 查找的值
    :return:
    """
    left = 0  # 列表起始索引
    right = len(li) - 1  # 列表最后一个元素的索引
    while left <= right:  # 候选区有值
        mid = (left + right) // 2
        if li[mid] == val:  # 找到元素返回元素索引位置
            return mid
        elif li[mid] > val:  # 待查找的值在mid左侧
            right = mid - 1
        else:  # li[mid] < val 待查找的值在mid右侧
            left = mid + 1
    else:
        return

二、排序

冒泡、选择和插入排序属于基础排序，为了降低干扰，所有的排序都默认使用升序。

2.1、冒泡排序(Bubble Sort)

基本思想：

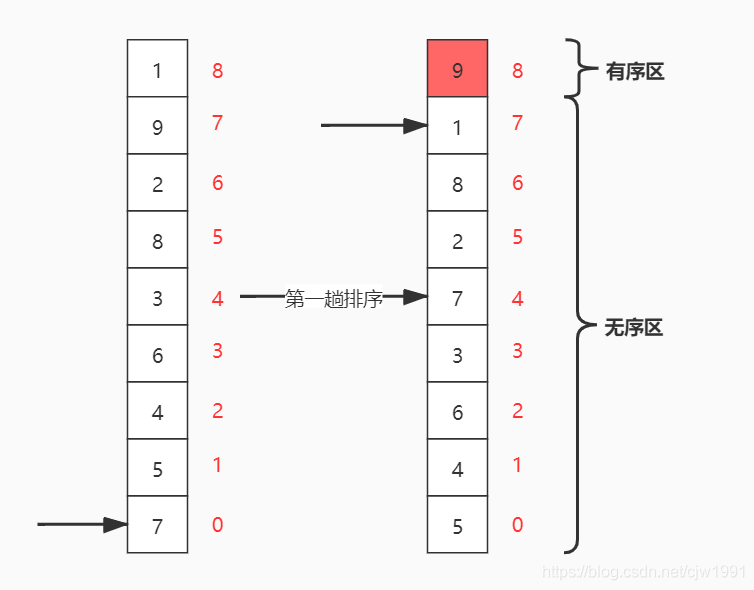
列表每两个相邻的数，如果前面比后面大，则交换这两个数。
一趟排序完成后，则无序区减少一个数，有序区增加一个数。
代码关键点：排序多少趟，无序区范围

时间复杂度：O(n²)
在这里插入图片描述

def bubble_sort(li):
	"""
	冒泡排序，默认升序
	:param li: 排序的列表
	:return:
	"""
	length = len(li)  # 列表长度
	# 冒泡排序剩余最后一个列表元素就不需要排序了，所以趟数是：length -1
	# range范围[0,length -1),
	for i in range(length - 1):  # 第i趟
		# 每一趟排序无序区减少一个元素，第i趟，无序区还剩元素range元素索引length - i
		# 由于是相邻元素对比，每次索引只到倒数第二个索引位置，就可以了，所以排序次数还需要-1
		exchange = False  # 标志位：记录无序区是否进行过元素的交换
		for j in range(length - i - 1):  # 第i趟无序区排序次数
			if li[j] > li[j + 1]:  # 升序
				li[j], li[j + 1] = li[j + 1], li[j]
				exchange = True

		# 如果一趟排序下来元素没有发生交换，那么列表已经排序完成，退出函数
		if not exchange:
			return
		print(f'第{i + 1}趟排序的结果：{li}')  # 打印每一次排序的结果


if __name__ == '__main__':
	# t_li = [7, 5, 4, 6, 3, 8, 2, 9, 1]
	t_li = [9, 8, 7, 6, 1, 2, 3, 4, 5]
	print(f'初始的列表：{t_li}')
	bubble_sort(t_li)
	print(f'排序后列表：{t_li}')

测试运行结果：

初始的列表：[9, 8, 7, 6, 1, 2, 3, 4, 5]
第1趟排序的结果：[8, 7, 6, 1, 2, 3, 4, 5, 9]
第2趟排序的结果：[7, 6, 1, 2, 3, 4, 5, 8, 9]
第3趟排序的结果：[6, 1, 2, 3, 4, 5, 7, 8, 9]
第4趟排序的结果：[1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后列表：[1, 2, 3, 4, 5, 6, 7, 8, 9]

2.2、选择排序(Select Sort)

简单的选择排序，便于理解

def select_sort_simple(li):
	"""
	简单的选择排序，循环初始列表，每次找到最小的一个元素，放进一个新列表中
	并删除原列表当前这个最小值
	:param li: 
	:return: 
	"""
	li_new = []
	for i in range(len(li)):
		min_val = min(li) # 找最小值，需要循环列表
		li_new.append(min_val)
		li.remove(min_val)
	return li_new

优化选择排序

一趟排序记录最小的数，放到第一个位置
再一趟排序记录列表无序区最小的数，放到第二个位置
…
算法的关键点：有序区和无序区、无序区最小值的位置

时间复杂度：O(n²)
在这里插入图片描述

def select_sort(li):
	"""
	选择排序
	:param li:
	:return:
	"""
	length = len(li)
	# 找无序区最小的值，无序区只剩最后一个元素不需要处理，所以需要n-1趟(初始状态整个列表都是无序区)
	# 找到无序区需要的最大或最小值，放到列表左侧的有序区
	for i in range(length - 1):  # 第i趟
		min_loc = i  # 默认无序区第一个元素为最小值
		# 每趟过后，无序区中所剩的元素，查找最小值。从无序区第二个位置开始查找比对
		for j in range(i + 1, length):
			if li[j] < li[min_loc]:
				min_loc = j
		# 交换无序区第一个元素和最小元素的值
		li[i], li[min_loc] = li[min_loc], li[i]
		print(f'第{i + 1}趟选择排序结果：{li}')


if __name__ == '__main__':
	t_li = [6, 4, 2, 3, 1, 5, 8, 9, 7]
	print(f'初始的列表：{t_li}')
	select_sort(t_li)
	print(f'排序的结果：{t_li}')

运行后的结果

初始的列表：[6, 4, 2, 3, 1, 5, 8, 9, 7]
第1趟选择排序结果：[1, 4, 2, 3, 6, 5, 8, 9, 7]
第2趟选择排序结果：[1, 2, 4, 3, 6, 5, 8, 9, 7]
第3趟选择排序结果：[1, 2, 3, 4, 6, 5, 8, 9, 7]
第4趟选择排序结果：[1, 2, 3, 4, 6, 5, 8, 9, 7]
第5趟选择排序结果：[1, 2, 3, 4, 5, 6, 8, 9, 7]
第6趟选择排序结果：[1, 2, 3, 4, 5, 6, 8, 9, 7]
第7趟选择排序结果：[1, 2, 3, 4, 5, 6, 7, 9, 8]
第8趟选择排序结果：[1, 2, 3, 4, 5, 6, 7, 8, 9]
排序的结果：[1, 2, 3, 4, 5, 6, 7, 8, 9]

2.3、插入排序(Insert Sort)

基本思想

初始时手里(有序区)只有一张牌
每次(从无序区)摸一张牌，插入到手里已有牌的正确位置
关键点：如何移动有序区中的元素位置，插入正确的位置

时间复杂度：O(n²)

在这里插入图片描述

def insert_sort(li):
	"""
	插入排序
	:param li:
	:return:
	"""
	length = len(li)
	for i in range(1, length):  # i 表示摸到的牌的下标，默认第一个元素为手里有序区的牌
		j = i - 1  # j 指的是手里有序区最后一张牌
		tmp = li[i] # 无序区第一个元素，摸到的牌
		while j >= 0 and li[j] > tmp:  # 有序区中找到比摸到牌大的元素
			li[j + 1] = li[j]  # 有序区的元素往右移动
			j -= 1
		li[j + 1] = tmp  # 移动完成后，摸到的牌插入到有序区
		print(f'第{i}次摸牌插入元素后的列表：{li}')


if __name__ == '__main__':
	t_li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
	print(f'初始的列表：{t_li}')
	insert_sort(t_li)
	print(f'排序后列表：{t_li}')

运行后的结果

初始的列表：[5, 7, 4, 6, 3, 1, 2, 9, 8]
第1次摸牌插入元素后的列表：[5, 7, 4, 6, 3, 1, 2, 9, 8]
第2次摸牌插入元素后的列表：[4, 5, 7, 6, 3, 1, 2, 9, 8]
第3次摸牌插入元素后的列表：[4, 5, 6, 7, 3, 1, 2, 9, 8]
第4次摸牌插入元素后的列表：[3, 4, 5, 6, 7, 1, 2, 9, 8]
第5次摸牌插入元素后的列表：[1, 3, 4, 5, 6, 7, 2, 9, 8]
第6次摸牌插入元素后的列表：[1, 2, 3, 4, 5, 6, 7, 9, 8]
第7次摸牌插入元素后的列表：[1, 2, 3, 4, 5, 6, 7, 9, 8]
第8次摸牌插入元素后的列表：[1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后列表：[1, 2, 3, 4, 5, 6, 7, 8, 9]