树的概念及其理解

1.树的概念

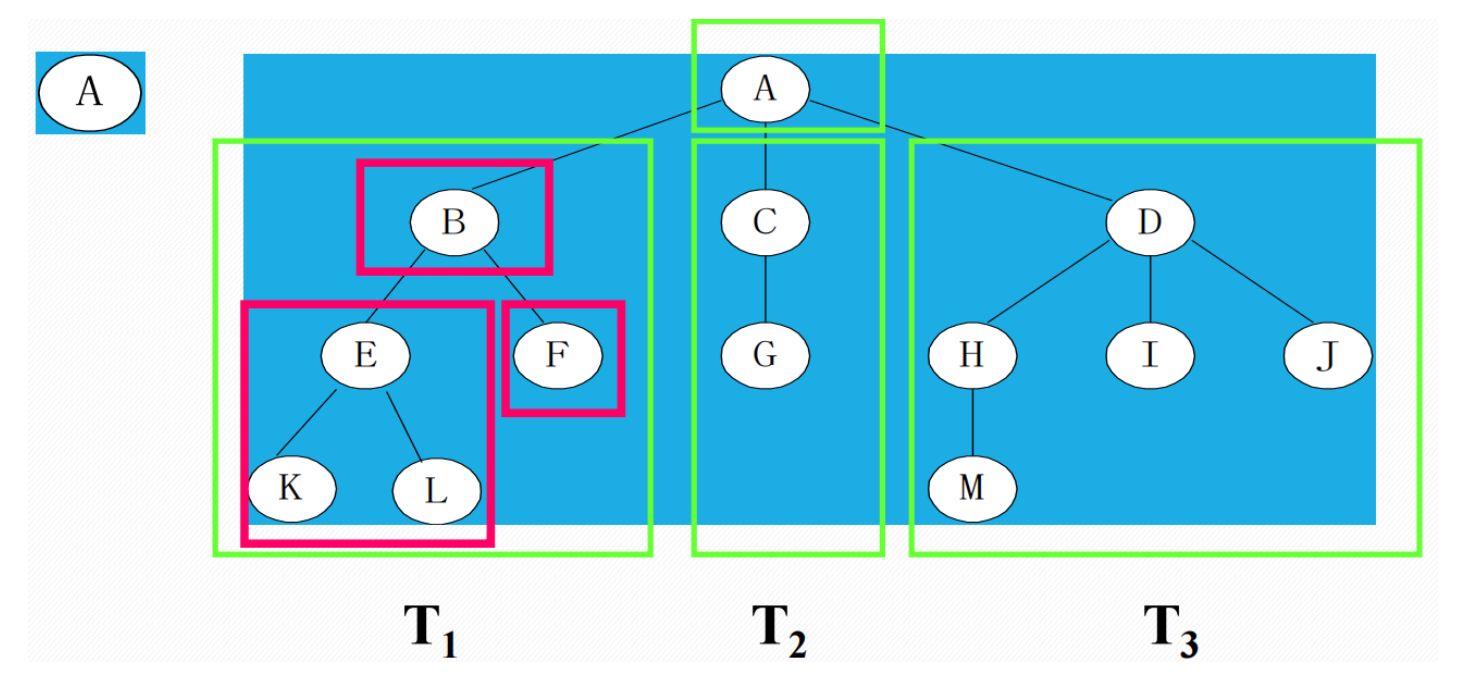
    树（Tree）是n（n>=0）个结点的有限集，它或为空树（n = 0）；或为非空树，对于非空树 T：

• 有且只有一个称之为根的结点
• 除根节点以外的其他结点可分为m（m>0）个互不相交的有限集T1, T2, T3 ...，Tm，其中每个结合本身也是一颗树，并且称之为根的子树（SubTree）

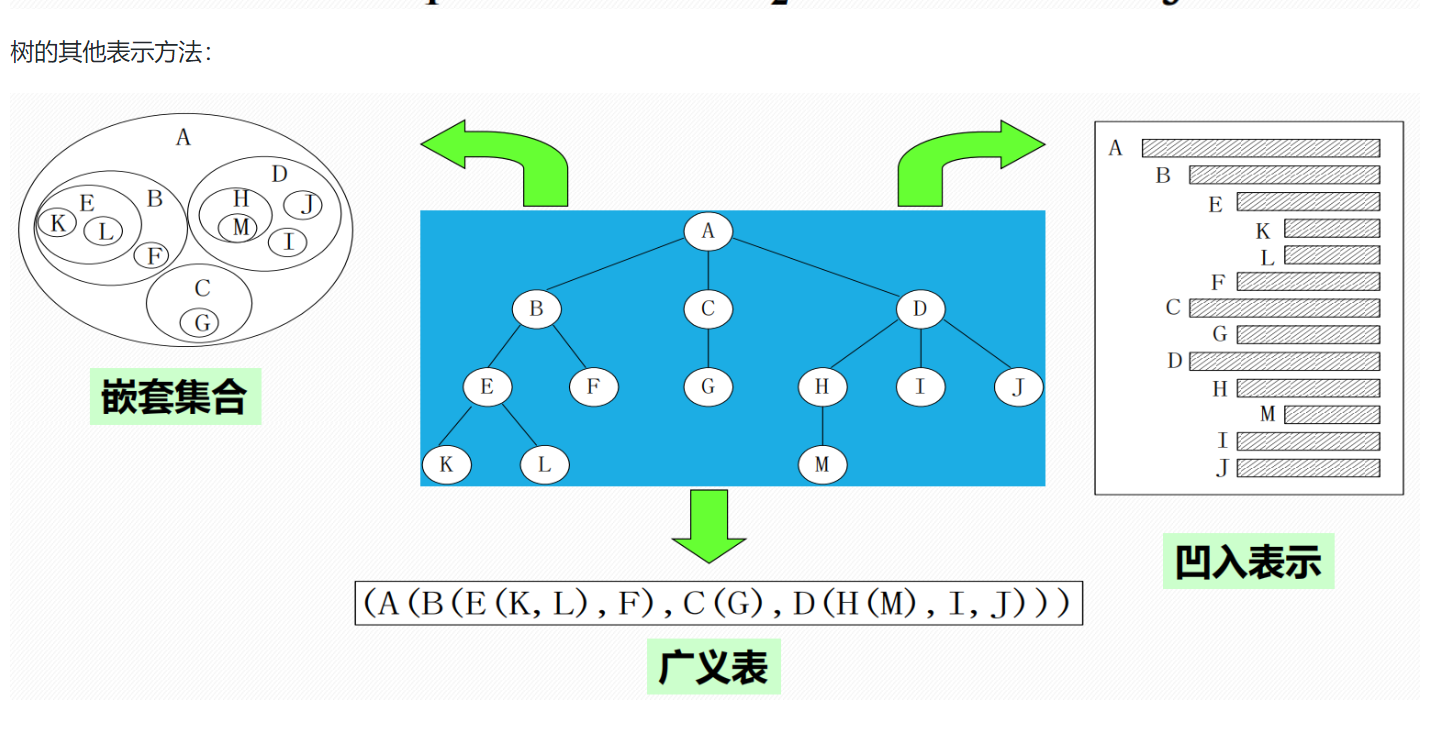
2 树的相关术语

1、结点的度

一个结点含有的子树的个数称为该结点的度。

2、叶子结点

度为0的结点称为叶结点，也可以叫做终端结点，叶子结点没有直接后继。

3、分支结点

度不为0的结点称为分支结点，也可以叫做非终端结点。

4、结点的层次

从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推

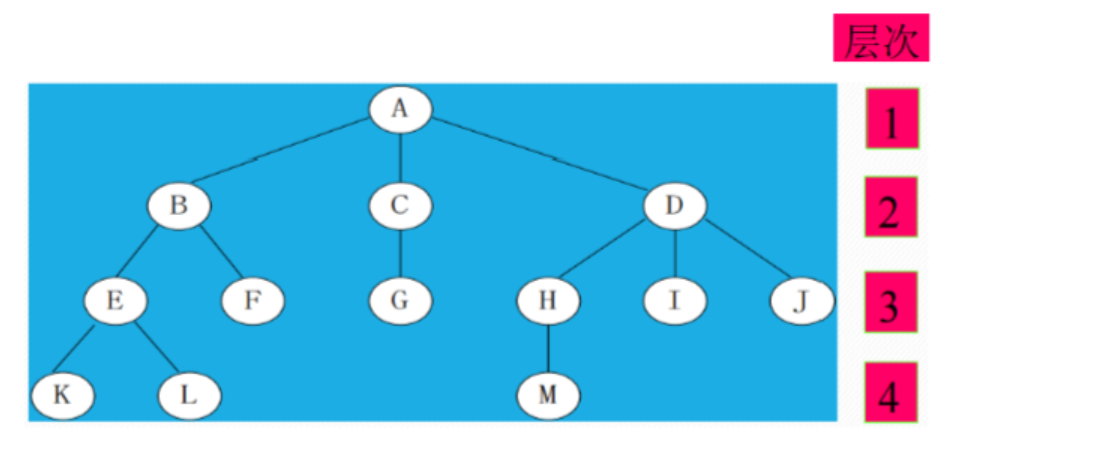
5、树的度

树中所有结点的度的最大值。

6、树的高度(深度)

树中结点的最大层次。

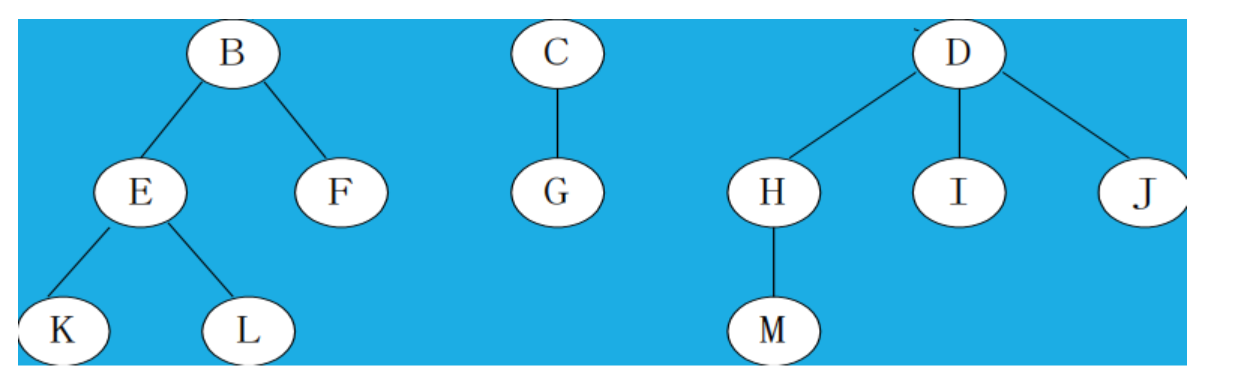
7、森林

m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根结点，森林就变成一棵树。

8、孩子结点

一个结点的直接后继结点称为该结点的孩子结点。

9、双亲结点(父结点)

一个结点的直接前驱称为该结点的双亲结点。

10、兄弟结点

同一双亲结点的 孩子结点间互称兄弟结点。

3. 二叉树

  1. 二叉树的概念

  二叉树就是度不超过2的树(每个结点最多有两个子结点)。

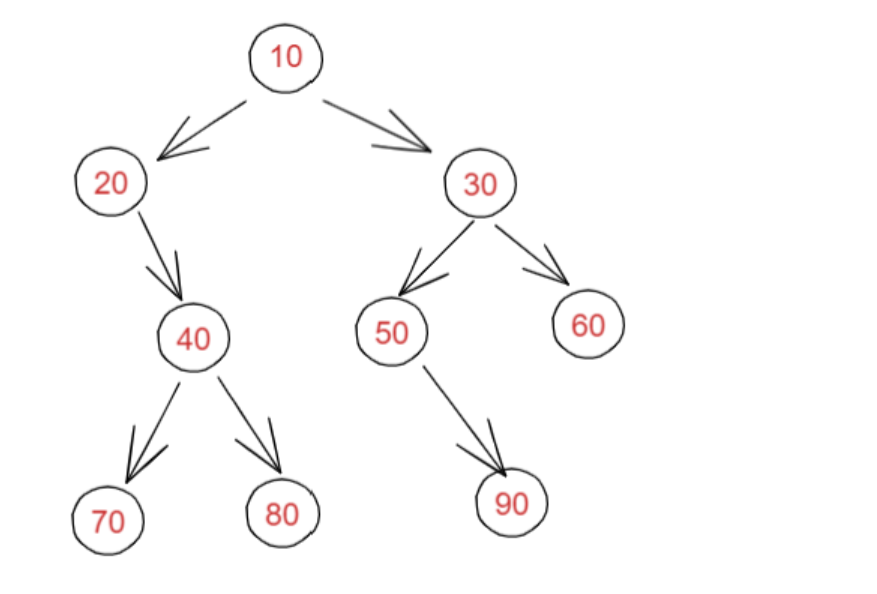
2 .二叉树的基本性质

1、在二叉树的第i层上最多有 2^(i-1) 个结点

2、深度为K的二叉树最多有 2^k - 1个结点

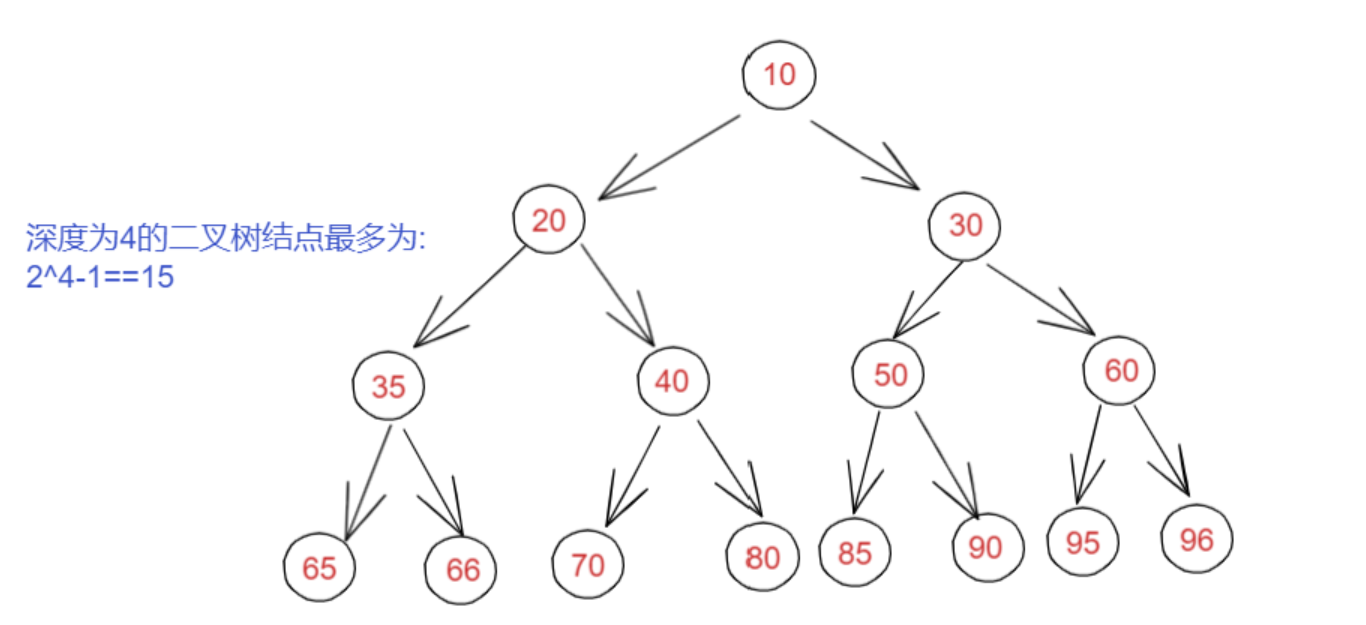
3、深度为K时最少有K个结点（每层1个结点）

3. 特殊形态的二叉树

1、满二叉树

一个二叉树，每层的结点树都达到最大值，则这个二叉树就是满二叉树。深度为K的满二叉树有 2^k - 1个结点。

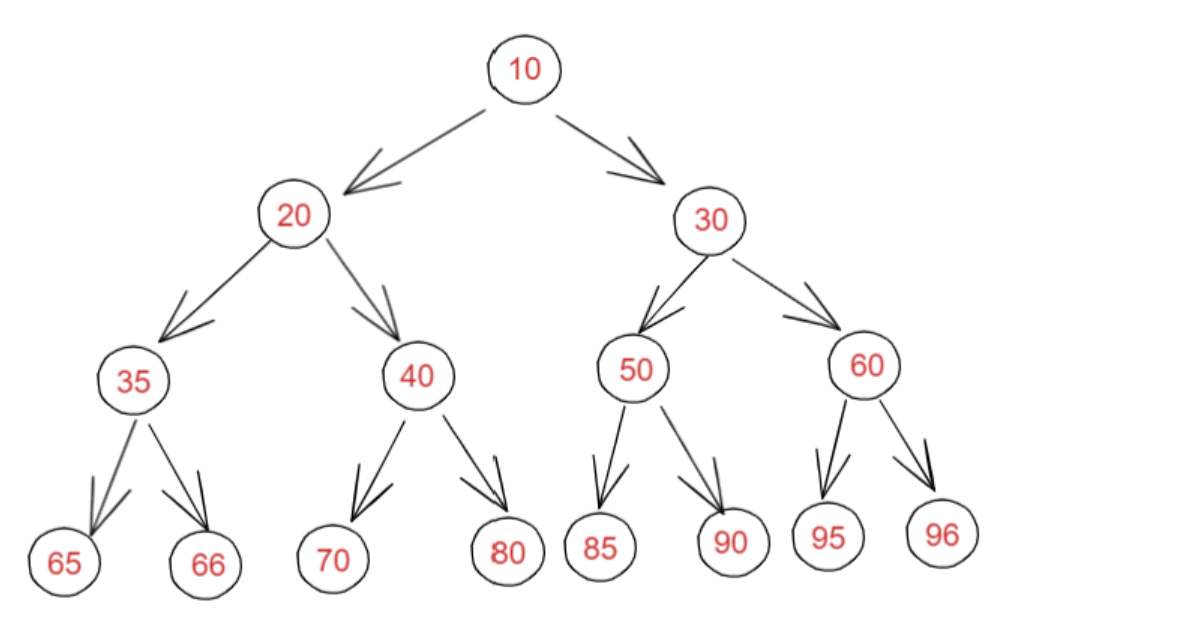
2、完全二叉树

叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

以下二叉树均为完全二叉树：

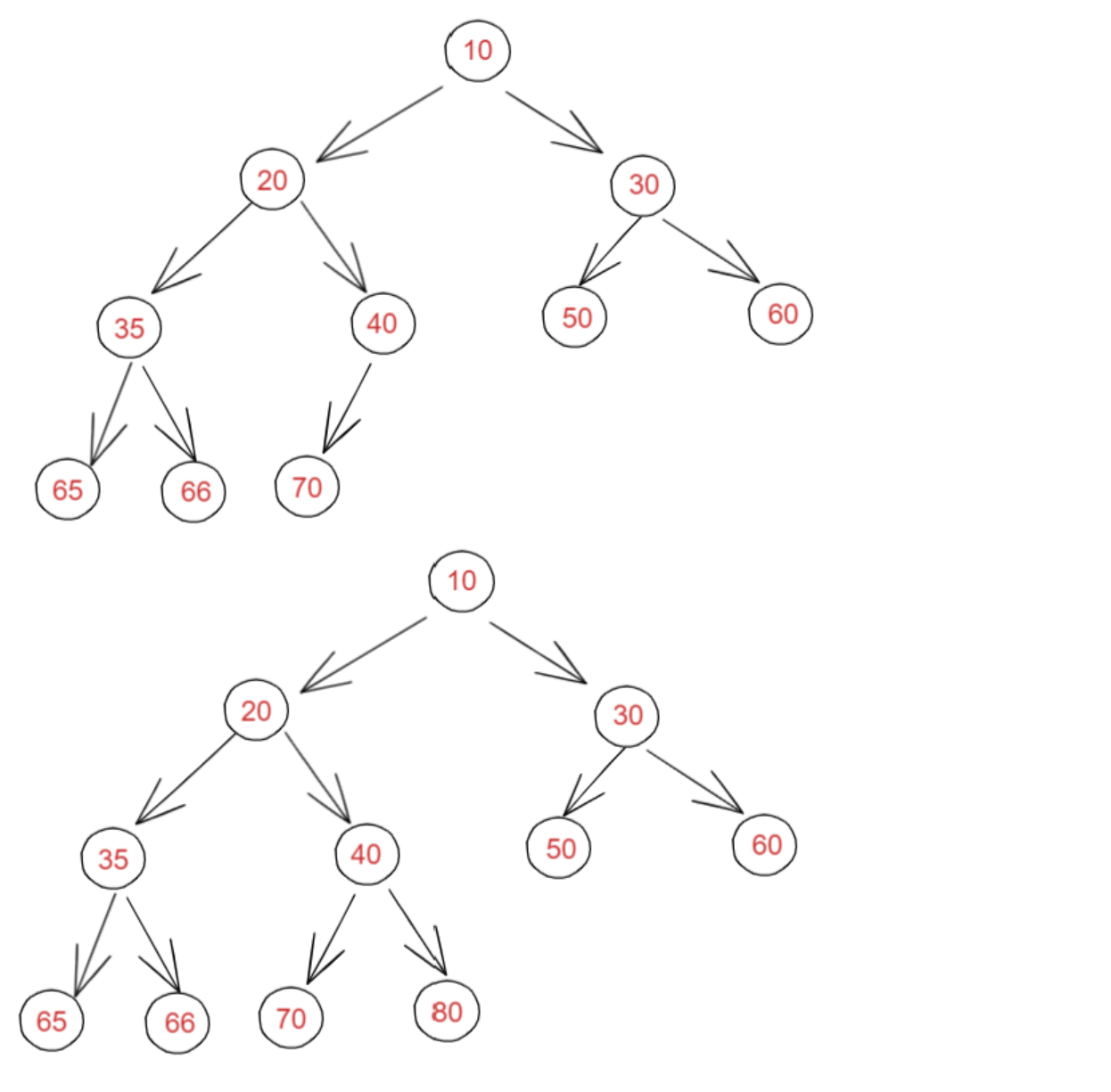
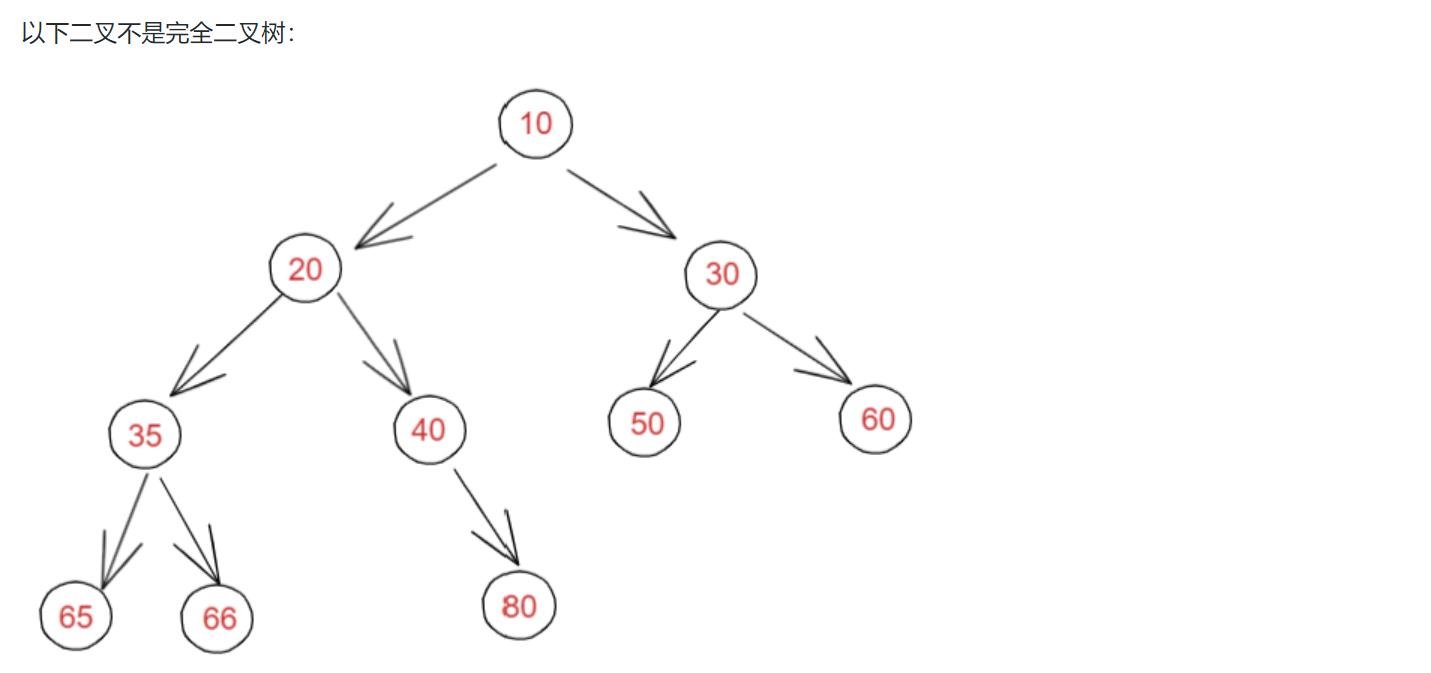
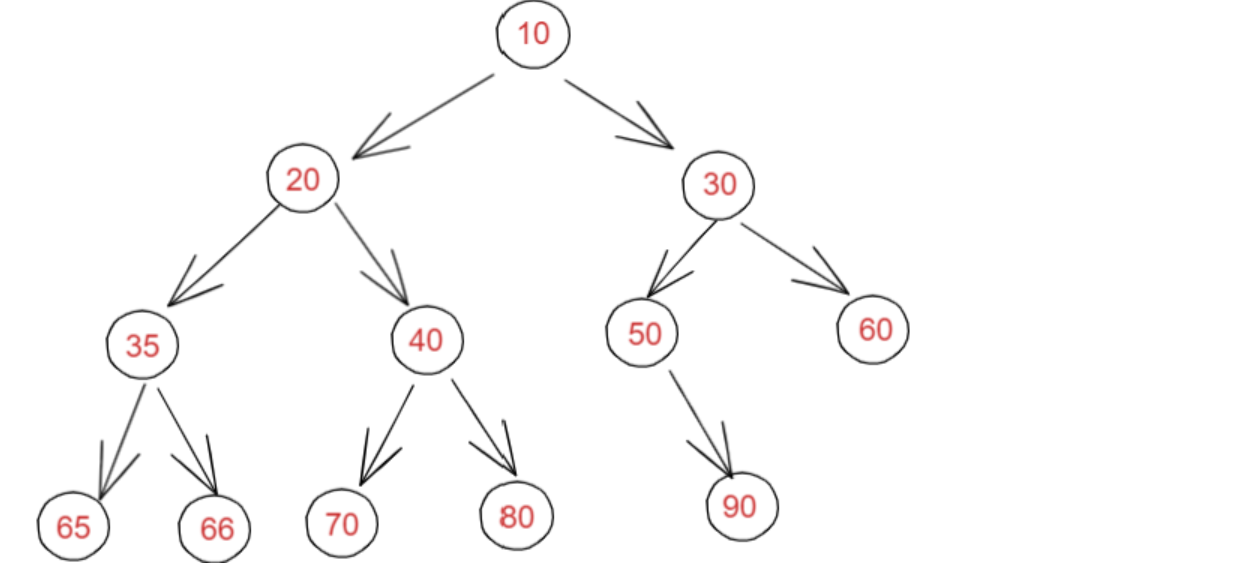
4. 二叉树的遍历

在对二叉树元素进行访问、插入、删除等操作时，我们需要对二叉树进行遍历，所谓的遍历指按某条搜索路线遍访每个结点且不重复(又称周游)。

对二叉树的遍历可以按照如下两种思路进行：

• 广度遍历：按层次遍历
• 深度遍历：
  • 前序（先序）遍历：根结点 ---> 左子树 ---> 右子树
  • 中序遍历：左子树---> 根结点 ---> 右子树
  • 后序遍历：左子树 ---> 右子树 ---> 根结点

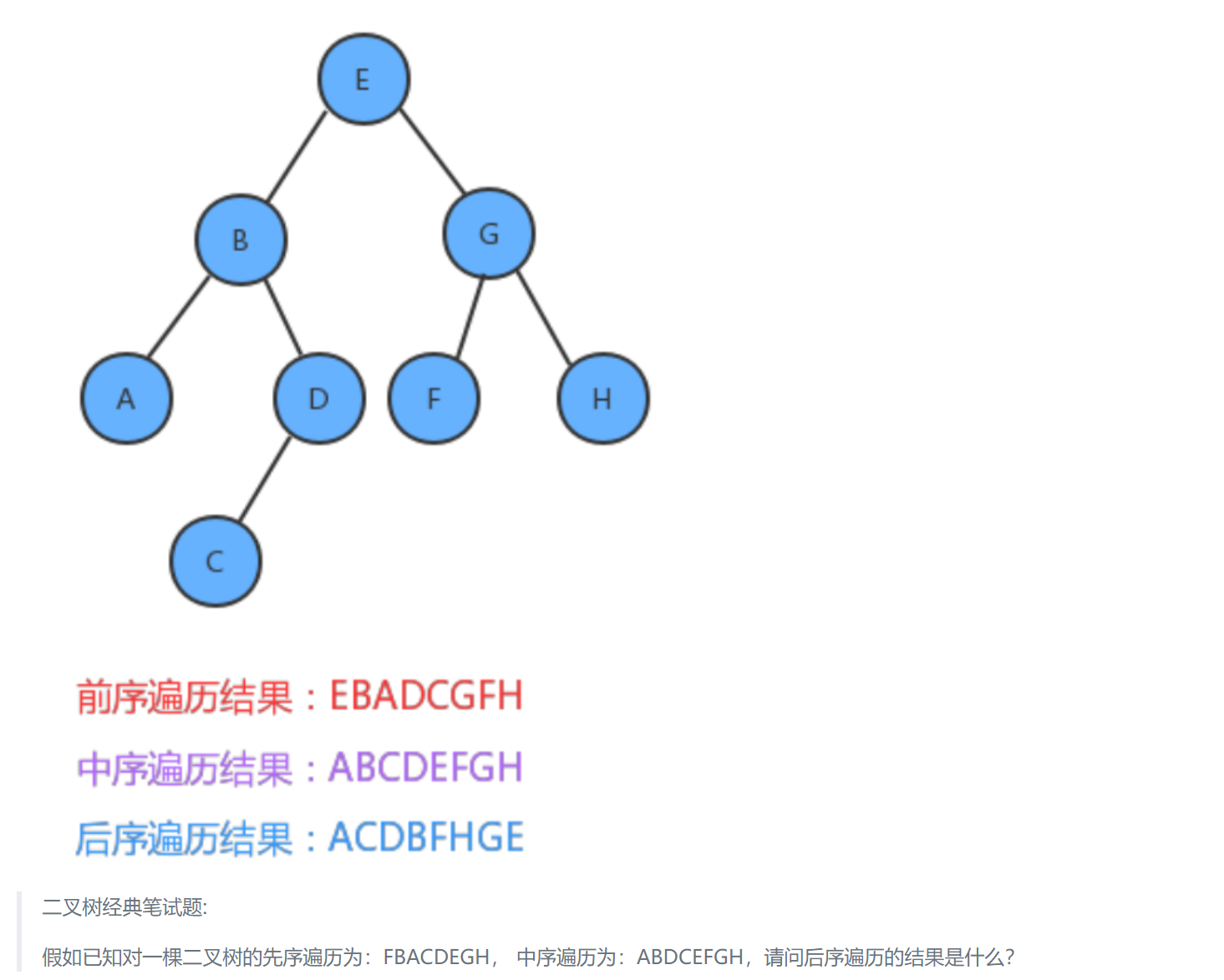
5. 二分查找树（二叉排序树）

1、二分查找树的概念

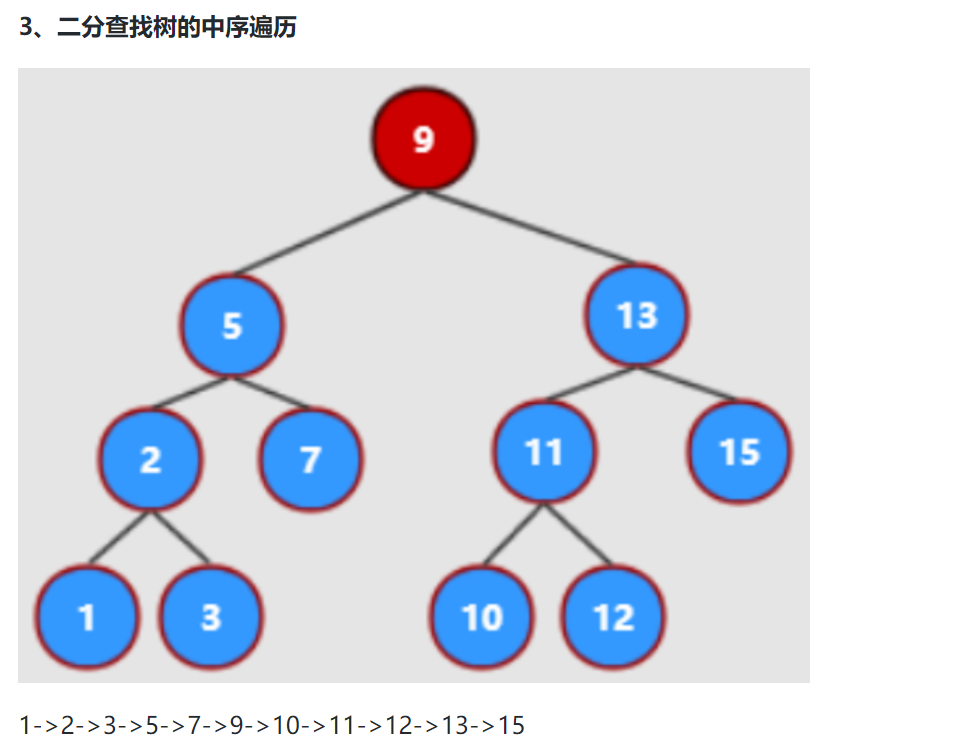
二分查找树BST（也叫二分查找树、二叉排序树）的提出是为了提供查找效率，之所以称为二分查找树，因为该二叉树对应着二分查找算法，查找平均的时间复杂度为O(logn)，所以该数据结构的提出是为了提高查找效率。

2、二分查找树的性质

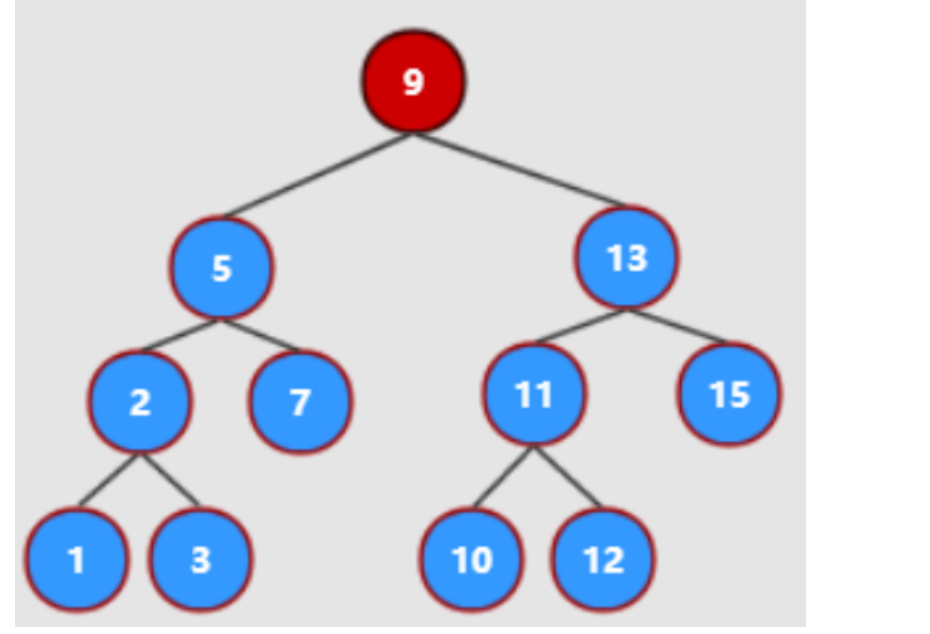
二分查找树具有下列性质：

• 若它的左子树不为空，则左子树上所有结点的值均小于根结点的值
• 若它的右子树不为空，则右子树上所有结点的值均大于根结点的值
• 它的左右子树均为二分查找树

4. 平衡二叉树

1. 平衡二叉树概述

1、引入

之前我们学习过二叉查找树，发现它的查询效率比单纯的链表和数组的查询效率要高很多，最理想的情况下时间复杂度可以达到O(logn)，大部分情况下，确实是这样的，但不幸的是，在最坏情况下，二叉查找树的性能还是很糟糕。

例如我们依次往二叉查找树中插入9,8,7,6,5,4,3,2,1这9个数据，那么最终构造出来的树是长得下面这个样子：

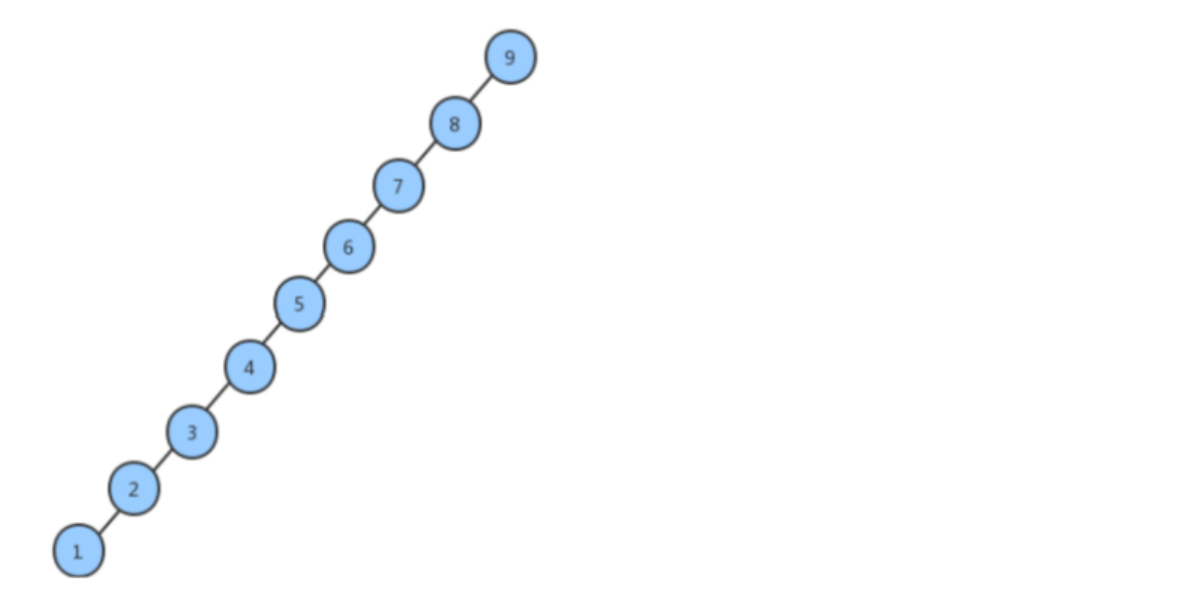
在极端的情况下，二分查找树可能会退化成为链表，我们会发现，如果我们要查找1这个元素，查找的效率依旧会很低。效率低的原因在于这个树并不平衡，全部是向左边分支，如果我们能够把这棵二分查找数进行调整让左右子树的高度相等，并且左右子树的结点数也趋近于相等，那么查找效率就会大大提高，我们可以将这棵树调整成为一棵平衡二叉树。

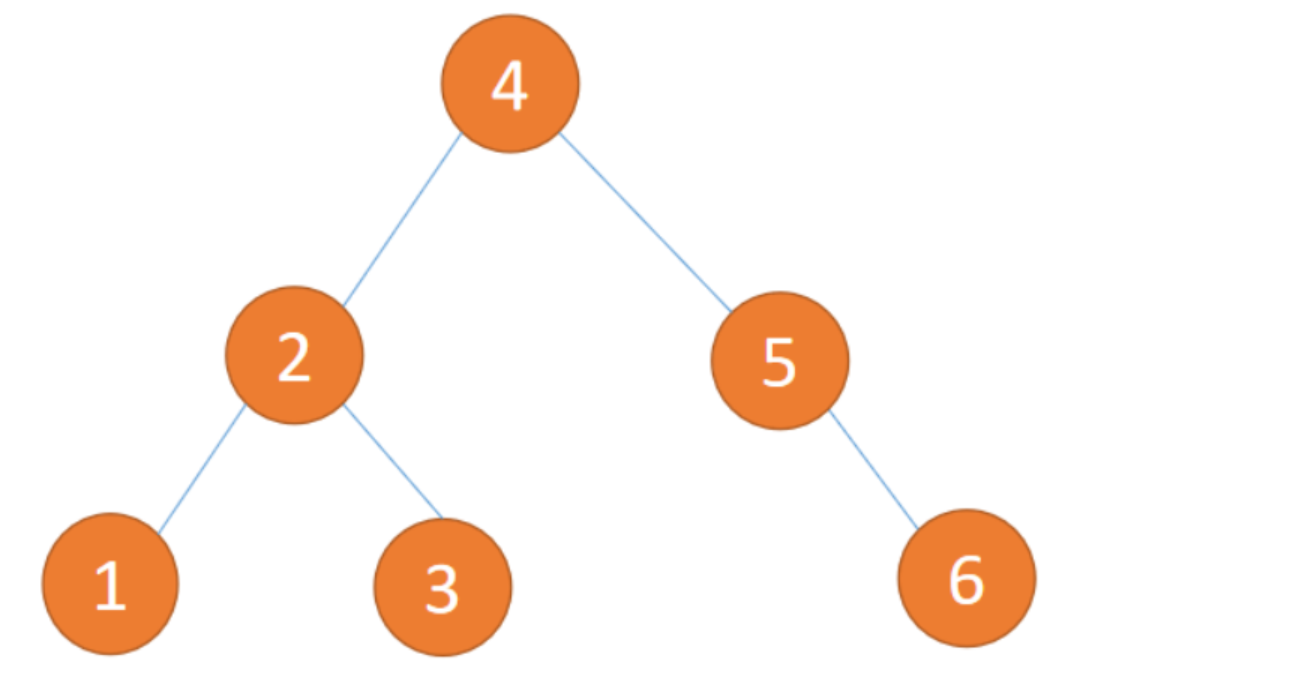
2、平衡二叉树的概念

平衡二叉树是一种二叉排序树，其中每一个结点的左子树和右子树的高度差至多等于1，平衡二叉树又称为AVL树。平衡二叉树是一种高度平衡的二叉排序树，意思是说，要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

3、平衡因子

平衡因子（BF，Balance Factor 而不是 Boy Friend）指的是：左子树和右子树高度差。一般来说 BF 的绝对值大于 1，,平衡树二叉树就失衡，需要「旋转」纠正。

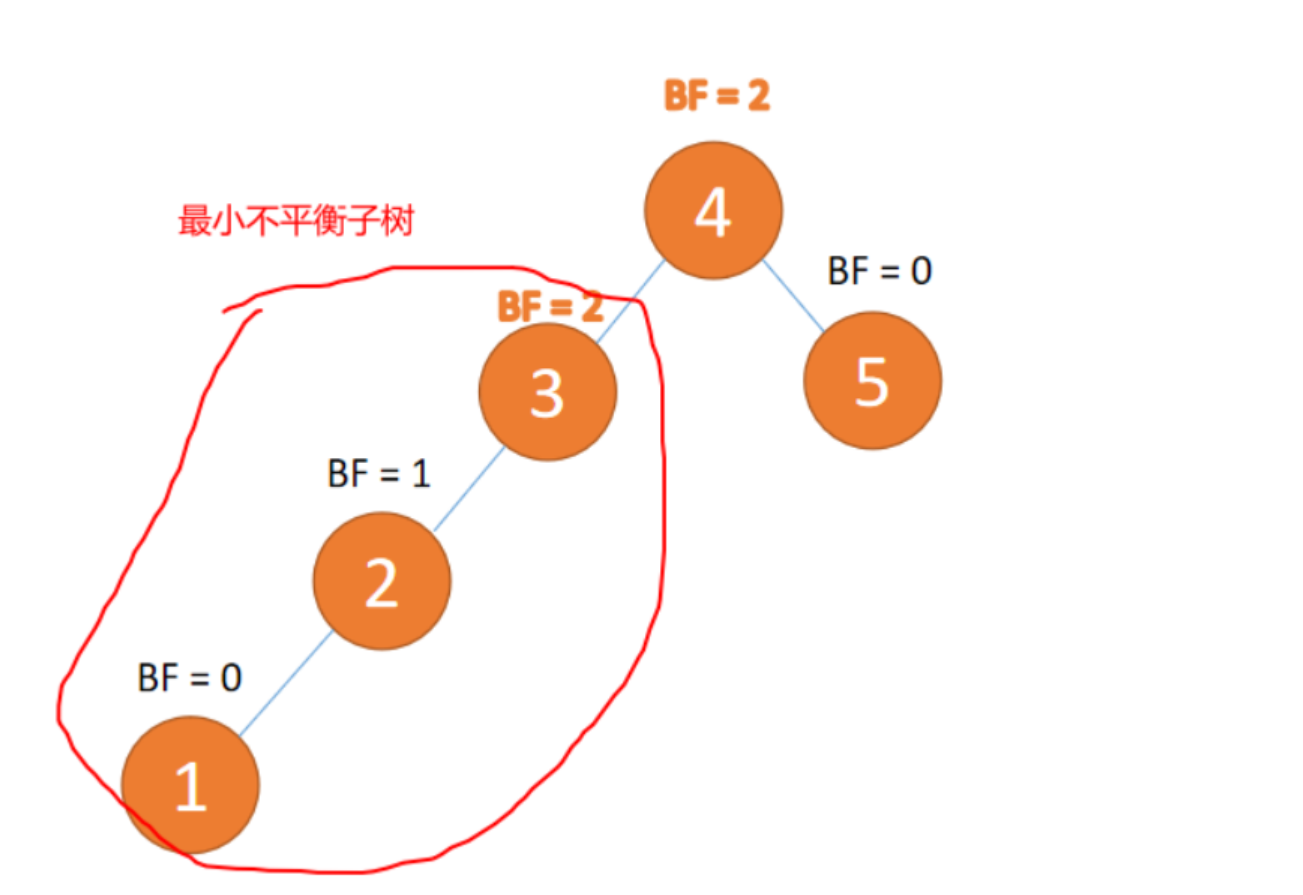
4、最小失衡子树/最小不平衡子树

距离插结点点最近的，并且 BF 的绝对值大于 1 的结点为根节点的子树叫做最小失衡子树。