目录
第一题 1482. 制作 m 束花所需的最少天数 - 力扣(LeetCode)
第四题 1254. 统计封闭岛屿的数目 - 力扣(LeetCode)
前言
本博客是记录和分享笔者写过的一些算法题,在帮助自己梳理思路的同时分享给愿意看的人,这些题目笔者认为值得一写,让我们一起进步,提高代码能力!
如标题所示, 这一期分享一些笔者写过的 关于单调栈,简单DFS,BFS和二分的题目,题目来源主要是蓝桥云的题库和力扣.
笔者并非是大牛,部分题解参考和模仿了大佬的写法,感谢那些愿意分享题解和思路的大佬!!!
第一题 1482. 制作 m 束花所需的最少天数 - 力扣(LeetCode)
涉及的知识点:二分查找答案减少时间复杂度

这道题需要我们去求等待的最少天数,很明显是需要我们枚举出一些可能的天数,看看是否符合题意,这样的话,我们可以使用二分算法去枚举可能的天数,然后根据题意模拟一遍,知道找到最小的而且符合的天数.
关于左右边界的确定,不需要直接套模板,因为根据题意,左边界肯定是bloomDay数组的最小值,右边界同理,最大值,这样就减少了二分查找的次数,而根据示例二,我们可以提前判断是否可以制作出足够数量的花束.
以下是笔者的代码:
class Solution {
public int minDays(int[] bloomDay, int m, int k) {
if (m > bloomDay.length / k) {
return -1;
}
int low = Integer.MAX_VALUE, high = 0;
int length = bloomDay.length;
for (int i = 0; i < length; i++) {
low = Math.min(low, bloomDay[i]); // 左边边界
high = Math.max(high, bloomDay[i]); // 右边边界
}
while (low < high) {
int days = (high - low) / 2 + low;
if (canMake(bloomDay, days, m, k)) {
high = days;
} else {
low = days + 1;
}
}
return low;
}
public boolean canMake(int[] bloomDay, int days, int m, int k) {
int num = 0; // 要求的花的数量
int flowers = 0; // 能连续的花的数量
int length = bloomDay.length;
for (int i = 0; i < length && num < m; i++) {
if(bloomDay[i]<=days)
{
flowers++;
if(flowers==k)
{
num++;
flowers=0;
}
}
else
{
flowers = 0;
}
}
return num >= m;
}
}
其中这一段代码的思路是这样的:
public boolean canMake(int[] bloomDay, int days, int m, int k) {
int num = 0; // 要求的花的数量
int flowers = 0; // 能连续的花的数量
int length = bloomDay.length;
for (int i = 0; i < length && num < m; i++) {
if(bloomDay[i]<=days)
{
flowers++;
if(flowers==k)
{
num++;
flowers=0;
}
}
else
{
flowers = 0;
}
}
return num >= m;
}因为题目要求的是连续的花朵,遍历数组,如果符合条件就让 flowers 增加,如果等于了要求的数量,num增加,flowers重新归零,但是,因为要求是连续的,假设在flowers的大小没有到达K之前,就已经出现了天数不够的情况,flowers要立刻归零,这样才能体现出要求连续的花朵.
本题强化了笔者对于二分算法的理解和使用
第二题 962. 最大宽度坡 - 力扣(LeetCode)
考察了使用单调栈解题.

首先,这一题当然可以使用暴力算法,直接 外层 for循环,内存for循环,然后维护最大值. 这样的的确确可以写出来,但是时间复杂度是 O(n^2) 所以,笔者介绍另一种思路
1.首先,我们构建一个单调递减的栈,
它的核心作用是:
在数组 A 中,找到当前元素 A[j] 在它左侧最小的元素 A[i],并保证索引 i<j
但是!它不是简单的存储最小值,它实际上存储的是:
数组中"最有可能形成最大坡宽"的起点索引 i,因为我们要保证宽距 j-i尽可能的大!
所以:
- 我们在遍历数组时,必须优先保留最小值,同时保证索引靠前。
- 这就导致了:
- 如果当前元素 A[i]≥A[stack.peek()] ,说明当前元素不会成为坡起点,直接跳过
自己想想很简单,我比你小,还比你靠左,为什么要选你不选我?肯定是选我呀.
代码如下:
class Solution {
public static int maxWidthRamp(int[] A) {
int n = A.length;
Stack<Integer> stack = new Stack<>(); // 维护一个单调递减栈,存索引
int maxWidth = 0;
// **1. 先构造单调递减栈,存储可能的 i**
for (int i = 0; i < n; i++) {
if (stack.isEmpty() || A[stack.peek()] > A[i]) {
stack.push(i);
}
}
// **2. 从后往前遍历 j,找到最大 j - i**
for (int j = n - 1; j >= 0; j--) {
while (!stack.isEmpty() && A[stack.peek()] <= A[j]) {
int i = stack.pop();
maxWidth = Math.max(maxWidth, j - i);
}
}
return maxWidth;
}
}第三题 3.星际旅行 - 蓝桥云课
考察了图的存储和简单BFS.

首先,根据题意,使用邻接表方式建图是比较合适的,然后通过BFS算法,去查找 y消耗之前,我们可以去多少星球, 邻接表的数据结构和 哈希的散列表类似,都是一个"链表数组"
"链表数组",即 数组的每个元素都是链表的数组.
代码如下:
import java.util.*;
import java.math.*;
public class Demo31
{
static int n, m, Q;
static ArrayList<ArrayList<Integer>> graph = new ArrayList<>(); // 邻接表方式建图
static double ans = 0;
public static int bfs(int start,int maxstep)
{
Queue<int []> queue = new LinkedList<>();
boolean[] visited = new boolean[n + 1];
queue.offer(new int[]{start,0}); // 把起点加入队列,起点还未移动过,因此步数为0 // 这个新初始化的数组表示什么? start 表示点,0表示用了多少步数
int count = 1;
visited[start] = true;//start 这个点已经走过了
while(!queue.isEmpty())
{
int [] cur = queue.poll();
int node = cur[0];//点的位置
int step = cur[1];//步数
if(step<maxstep) // 步数小于最大步数
{
for(int nei : graph.get(node)) // 遍历以node为头结点的链表,也就是node 的相邻节点
{
if(visited[nei]==false)
{
visited[nei] =true;
count++;
queue.offer(new int[]{nei,step+1});
}
}
}
}
return count;
}
public static void main(String[] args) {
Scanner scanner =new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Q = scanner.nextInt();
graph.clear();
for(int i = 0;i<=n;i++)
{
graph.add(new ArrayList<>());
// 创建好 邻接表
}
for(int i =1;i<=m;i++)
{
int ai = scanner.nextInt();
int bi = scanner.nextInt();
graph.get(ai).add(bi);
graph.get(bi).add(ai);
}
for(int i = 1;i<=Q;i++)
{
int x = scanner.nextInt();
int y = scanner.nextInt();
// x 表示起始点,y表示最大步数
ans +=bfs(x,y);
}
System.out.printf("%.2f\n", ans / Q);
}
}
笔者的队列中放的是一个数组,这样的话,0下标可以表示位置,1下标可以表示步数,使用起来也相对简单
第四题 1254. 统计封闭岛屿的数目 - 力扣(LeetCode)
考察我们的搜索,笔者用的是DFS写法
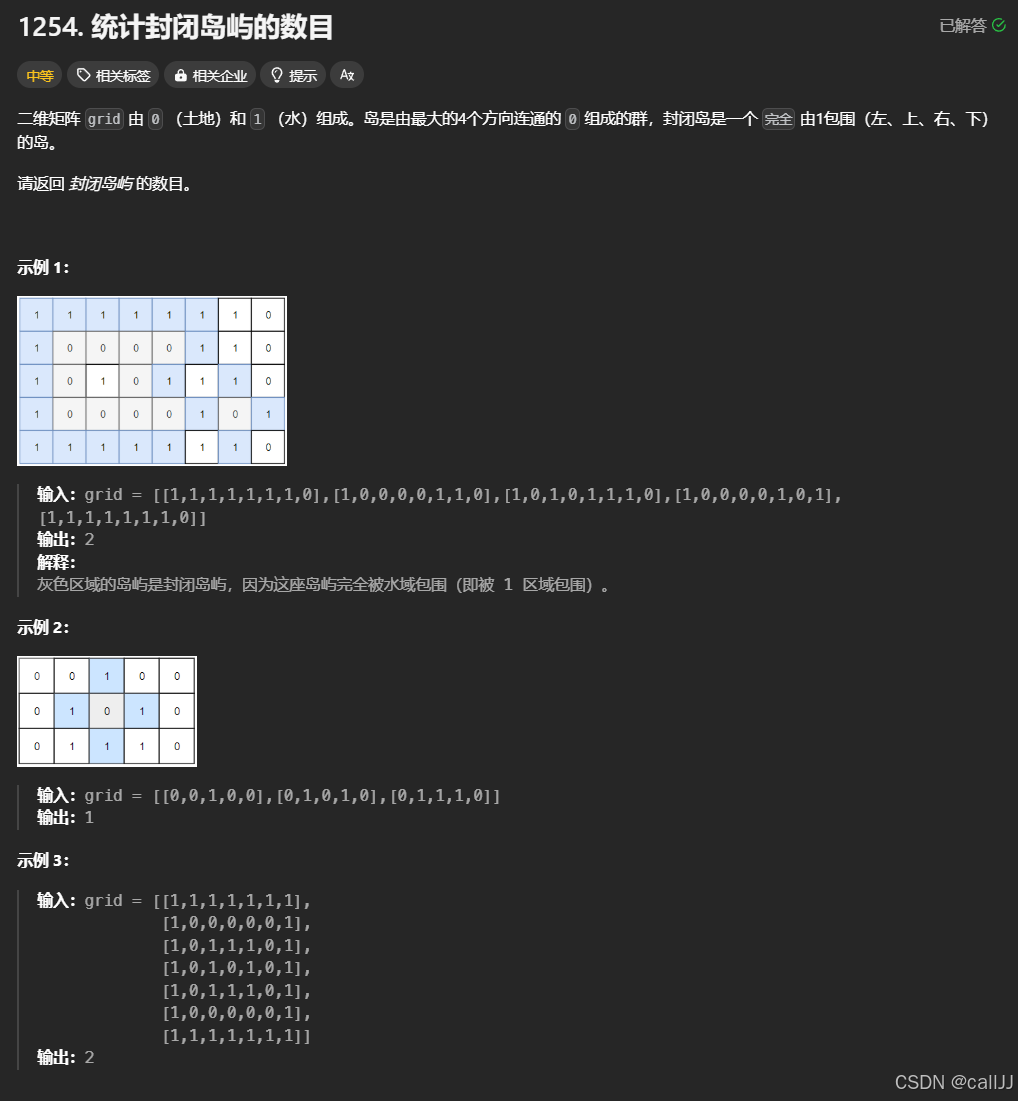
关于本题如何解,笔者认为,与其去找那些岛屿是封闭的,不如去找哪些岛屿不是封闭的
那么,什么样的岛屿不是封闭的呢?
答: 和边界有交界的岛屿不是封闭的,如果我们遍历图,将不是封闭的岛屿视作水,即0->1
然后去看看有多少封闭岛屿,这就转化为有多少岛屿的简单问题了
class Solution {
static boolean[][] vis;
static int[] dx = {1, -1, 0, 0};
static int[] dy = {0, 0, 1, -1};
static int res; // 封闭岛屿数量
static int X, Y; // 矩阵大小
public static void DFS(int x, int y, int[][] grid) {
vis[x][y] = true;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < X && ny >= 0 && ny < Y && !vis[nx][ny] && grid[nx][ny] == 0) {
DFS(nx, ny, grid);
}
}
}
public int closedIsland(int[][] grid) {
X = grid.length;
Y = grid[0].length;
vis = new boolean[X][Y];
res = 0;
// 1. 先遍历边界,把所有接触边界的 0 变为 1,防止误判
for (int i = 0; i < Y; i++) {
if (grid[0][i] == 0) DFS(0, i, grid); //把不是封闭的岛屿视作水
if (grid[X - 1][i] == 0) DFS(X - 1, i, grid);
}
for (int i = 0; i < X; i++) {
if (grid[i][0] == 0) DFS(i, 0, grid);
if (grid[i][Y - 1] == 0) DFS(i, Y - 1, grid);
}
// 2. 遍历所有的 0,找封闭岛屿
for (int i = 0; i < X; i++) {
for (int j = 0; j < Y; j++) {
if (!vis[i][j] && grid[i][j] == 0) {
res++; // 统计封闭岛屿
DFS(i, j, grid);
}
}
}
return res;
}
}结尾
博客到此结束,希望对看到这里的人有用,这不是题解,更像是笔者的推荐题.






















 1315
1315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








