堆排序详解-优快云博客

原文地址：http://blog.youkuaiyun.com/morewindows/article/details/6709644

http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。

二叉堆：

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆（大根堆）。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆（小根堆）。下图展示一个最小堆：

由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

注意：①堆中任一子树亦是堆。②以上讨论的堆实际上是二叉堆（Binary Heap），类似地可定义k叉堆。

1.堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

2.堆排序的思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

其基本思想为(大顶堆)：

1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];

3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

操作过程如下：

1)初始化堆：将R[1..n]构造为堆；

2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

下面举例说明：

给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

首先根据该数组元素构建一个完全二叉树，得到

然后需要构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：

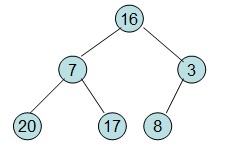
（a）（b）（c）

20和16交换后导致16不满足堆的性质，因此需重新调整

(d)

这样就得到了初始堆。

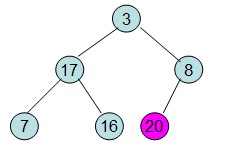
即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

此时3位于堆顶不满堆的性质，则需调整继续调整

这样整个区间便已经有序了。

从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

<pre name="code" class="cpp">/*堆排序(大顶堆) 2011.9.14*/ 

#include <iostream>
#include<algorithm>
using namespace std;

void HeapAdjust(int *a,int i,int size)  //调整堆 
{
    int lchild=2*i+1;       //i的左孩子节点序号 
    int rchild=2*i+2;     //i的右孩子节点序号 
    int max=i;            //临时变量 
    while(lchild<(size-1) && rchild<(size-1)) //非递归
    {
        if(a[lchild]>a[max]) //如果左孩子大于父节点
        {
            max=lchild;
        }    
        if(a[rchild]>a[max]) //如果右孩子大于当前最大节点（可能为父节点，或者左节点）
        {
            max=rchild;
        }
        if(max!=i) //如果父节点不是最大节点
        {
            swap(a[i],a[max]);
//            HeapAdjust(a,max,size);    //避免调整之后以max为父节点的子树不是堆 
            
            i = max;    //将互换过数据的子节点作为新的父节点以便迭代
            lchild = 2*i+1;
            rchild = 2*i+2;
        }
        else   //如果父节点是最大节点就不需要任何改动
            break;
    }        
}

void BuildHeap(int *a,int size)    //建堆 size为a[]数组长度
{
    int i = size/2 - 1;   //i是数组中数据的下标
    for(;i>=0;i--)        //从非叶节点开始，非叶节点最大的下标值为size/2 - 1 
    {
        HeapAdjust(a,i,size);    
    }    
} 

void HeapSort(int *a,int size)    //堆排序 
{
    BuildHeap(a,size);
    int i;   
    for(i=size-1;i>=0;i--)
    {
        swap(a[0],a[i]);           //交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面 
        HeapAdjust(a,0,i+1);      //重新调整堆顶节点成为大顶堆
    }
} 

int main(int argc, char *argv[])
{
    int a[]={0,16,20,3,11,17,8};
    int size = sizeof(a);
    int i;
    HeapSort(a,size);
    for(i=0;i<=size-1;i++)
        cout<<a[i]<<"";
    cout<<endl;
    return 0;
}

性能分析

调堆：如果初始数组是非降序排序，那么就不需要调堆，直接就满足堆的定义，此为最好情况，运行时间为Θ(1)；如果初始数组是如图1.5，只有A[0] = 1不满足堆的定义，经过与子节点的比较调整到图1.6，但是图1.6仍然不满足堆的定义，所以要递归调整，一直到满足堆的定义或者到堆底为止。如果递归调堆到堆底才结束，那么是最坏情况，运行时间为O(h) (h为需要调整的节点的高度，堆底高度为0，堆顶高度为floor(logn) )。

建堆(大根堆)完成之后，交换堆的第一个元素和堆的最后一个元素，然后堆的大小size减一，对大小为新size的堆进行调堆，如此循环，直到size== 1时停止，最后得出结果如图3。
建堆：每一层最多的节点个数为n1 = ceil(n/(2^(h+1))),

因此，建堆的运行时间是O(n)。

堆的操作——插入删除

下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解，再给出实现代码，最好是先看明白图后再去看代码。

堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。

最小堆的插入代码实现：

void MinHeapFixup(int *a, int i)
{
    int j, temp;
	j = (i-1)/2;
	temp = a[i];
	
	while(j>=0 && i!=0)
	{
	    if(a[j] <= a[i])
		    break;
		a[i] = a[j];
		i = j;
		j = (i-1)/2;
	}
	a[i] = temp;
}

void MinHeapAdd(int a[], int nNum)
{
    int len = sizeof(a)/sizeof(a[0]);
	a[len] = nNum;
	MinHeapFixup(a, len);
}

堆的删除

按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

//  从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
    int j, temp;

	temp = a[i];
	j = 2 * i + 1;
	while (j < n)
	{
		if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
			j++;

		if (a[j] >= temp)
			break;

		a[i] = a[j];     //把较小的子结点往上移动,替换它的父结点
		i = j;
		j = 2 * i + 1;
	}
	a[i] = temp;
}
//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{
	Swap(a[0], a[n - 1]);
	MinHeapFixdown(a, 0, n - 1);
}